опр. ОПР 2. Гармонический анализ периодичной последовательности прямоугольных импульсов, спектральный анализ импульса прямоугольной формы
 Скачать 368.79 Kb. Скачать 368.79 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра конструирования и производства радиоаппаратуры (КИПР) ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ, СПЕКТРАЛЬНЫЙ АНАЛИЗ ИМПУЛЬСА ПРЯМОУГОЛЬНОЙ ФОРМЫ Отчет по результатам учебной практики: ознакомительная (рассредоточенная) Обучающийся гр. 231-1 _____________С.В.Бальжинимаев (подпись) _____________ (дата) Руководитель практики от Университета: Преподаватель каф. КИПР _________ _____________Т.Н. Пушкарёв (оценка) (подпись) _____________ (дата) Томск 2022 Министерство науки и высшего образования Российской Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра конструирования и производства радиоаппаратуры (КИПР) УТВЕРЖДАЮ Зав. кафедрой КИПР __________ Кривин Н.Н. (подпись) «___» __________ 20__ г. ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ на учебную практику: ознакомительная (рассредоточенная) студенту гр. 231-1 радиоконструкторского факультета Бальжинимаеву Санжи Владимировичу 1. Тема практики:периодическая последовательность импульсов экспоненциальной формы и интегрирующая электрическая цепь 2-го порядка. 2. Цель практики закрепление на практике знаний, умений и навыков полученных в процессе теоретического обучения; развитие первичных навыков введения самостоятельной практической работы, исследования и анализа научных данных. 3. Задачи практики: развитие способности по осуществлению обработки и анализа информации полученных из прикладных компьютерных программ, представления ее в требуемом формате с использованием информационных и компьютерных технологий; развитие готовности формировать презентации, научно-технические отчёты по результатам выполненной работы. 4. Сроки прохождения практики: 09.02.2022 – 01.06.2022. Совместный рабочий график (план) проведения практики
Дата выдачи: «09» Февраля 2022 г. Руководитель практики от университета Преподаватель (должность) ___________________ (Подпись) Пушкарёв Т.Н. Задание принял к исполнению «28» Февраля 2021 г. Студент гр. 231-1 ___________________ Бальжинимаев С.В. (Подпись) ОглавлениеВведение 1. ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ 5 1.1. Сигнал 5 1.2. Тригонометрический ряд Фурье 5 1.2.1. Определение 5 1.2.2. Сходимость ряда Фурье 6 1.3. Гармонический анализ периодических сигналов 6 1.4. Периодическая последовательность прямоугольных импульсов 8 2. СПЕКТРАЛЬНЫЙ АНАЛИЗ ОДИНОЧНЫХ СИГНАЛОВ 11 2.1. Спектральный анализ непериодических сигналов 11 2.2. Импульс прямоугольной формы 13 Заключение 17 Список литературы 18 Введение Целью практики является закрепление на практике знаний, умений и навыков, полученных в процессе теоретического обучения. Развитие первичных навыков ведения самостоятельной практической работы, исследования и анализа научных данных. Задачей практики является развитие способностей по осуществлению обработки и анализа информации полученных из прикладных компьютерных программ, представления ее в требуемом формате с использованием информационных и компьютерных технологий. Развитие готовности формировать презентации, научно-технические отчеты по результатам выполненной работы. 1.ГАРМОНИЧЕСКИЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ 1.1 Сигнал Сигнал s(t) называется периодическим, если он удовлетворяет условию  , где m = 0,±, ±2,..., Т - наименьший интервал времени, через который мгновенные значения сигнала повторяются, называется этот интервал - периодом. Ставя задачу гармонического анализа периодического сигнала, будем представлять этот сигнал в виде суммы постоянной составляющей и гармонических составляющих с некоторыми амплитудами, частотами и начальными фазами. Совокупность указанных составляющих будем называть гармоническим спектром заданного периодического сигнала. , где m = 0,±, ±2,..., Т - наименьший интервал времени, через который мгновенные значения сигнала повторяются, называется этот интервал - периодом. Ставя задачу гармонического анализа периодического сигнала, будем представлять этот сигнал в виде суммы постоянной составляющей и гармонических составляющих с некоторыми амплитудами, частотами и начальными фазами. Совокупность указанных составляющих будем называть гармоническим спектром заданного периодического сигнала.Если s(t) является периодическим сигналом, то он не принадлежит пространству L2(—  , ,  ), поскольку для всякого периодического сигнала ), поскольку для всякого периодического сигнала 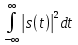 расходится (обращается в бесконечность), физический смысл — его энергия по области определения на бесконечном отрезке времени бесконечна. расходится (обращается в бесконечность), физический смысл — его энергия по области определения на бесконечном отрезке времени бесконечна.Однако, поскольку мгновенные значения периодического сигнала s(t) во времени повторяются через интервалы, равные периоду Т, то для полного описания периодического сигнала его достаточно задать на интервале (to, to + Т), где t0 — произвольный момент времени. Пусть, например, t0= —Т/2, тогда интервал, на котором полностью описан заданный сигнал, есть (—Т/2; Т/2). Если нас интересует изменение во времени сигнала вне этого интервала, то можно использовать свойство периодичности. Используя результаты, полученные при разложении в ряд Фурье сигналов на конечном интервале для периодического сигнала, можно сразу записать
1.2 Тригонометрический ряд Фурье 1.2.1 Определение Тригонометрическим рядом Фурье называют функциональный ряд вида 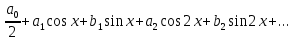 или более сжатого вида:
Постоянные числа  называются коэффициентами тригонометрического ряда. называются коэффициентами тригонометрического ряда.Если ряд (1.1) сходится, то его сумма есть периодическая функция f(x) с периодом 2π, так как 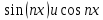 являются периодическими функциями с периодом 2π. являются периодическими функциями с периодом 2π.1.2.2. Сходимость ряда Фурье Теорема: Шаблон: Начало цитаты если периодическая функция f(x) с периодом 2π – кусочно-монотонная и ограниченна на отрезке  , то тригонометрический ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда s(x) равна значению функции f(x) в точках ее непрерывности. В точках разрыва f(x) сумма ряда равняется среднему арифметическому пределов функции f(x) справа и слева. Шаблон:Конец цитаты. , то тригонометрический ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда s(x) равна значению функции f(x) в точках ее непрерывности. В точках разрыва f(x) сумма ряда равняется среднему арифметическому пределов функции f(x) справа и слева. Шаблон:Конец цитаты.Из этой теоремы следует, что тригонометрические ряды Фурье применимы к достаточно широкому классу функций. 1.3 Гармонический анализ периодических сигналов Представление периодического сигнала в форме (1.2) удобно использовать, когда сигнал представляет собой периодическую последовательность, например, униполярных импульсов (рис. 1.1). В отличие от предыдущего случая, это выражение описывает сигнал на всей временной оси, что является следствием периодичности функций ортогонального базиса. И тогда можно использовать полученные ранее формулы:  . .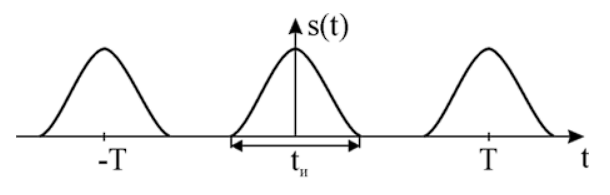 Рис. 1.1 Комплексная амплитуда гармонического колебания:  . . Можно использовать и тригонометрическую форму записи ряда Фурье
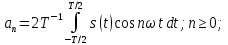  Через коэффициенты 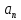 и и 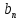 амплитуды и начальные фазы выражаются так: амплитуды и начальные фазы выражаются так:  . .Представление периодического сигнала в виде ряда (1.3) бывает удобным, когда функция s(t) обладает свойством четности или нечетности, так если 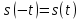 – четная функция, то все коэффициенты – четная функция, то все коэффициенты 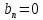 , а если , а если 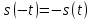 – нечетная функция, то – нечетная функция, то  . .Вычисление можно сделать более общим, если сигнал в виде импульса ограничен во времени, длительность tH - в пределах периода Т, форма импульсов одинакова, а период — произвольный, тогда удобно выполнить предварительные вычисления, найдя вспомогательную функцию 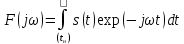 , которую называют спектральной функцией. , которую называют спектральной функцией.После ее вычисления можно, задавшись произвольной длительностью периода  , сразу найти , сразу найти  (вместо ω подставить nΩ), а постоянную составляющую найти так: (вместо ω подставить nΩ), а постоянную составляющую найти так: 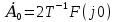 , т.е. прировнять ω к нулю. , т.е. прировнять ω к нулю.Чтобы задать спектр периодического сигнала, необходимо указать частоты гармонических составляющих сигнала и соответствующие этим частотам амплитуды и начальные фазы. При этом различают два понятия — амплитудный спектр сигнала — это совокупность частот и соответствующих им амплитуд гармонических составляющих и фазовый спектр — совокупность частот и соответствующих им начальных фаз гармонических составляющих. Понятие амплитудного спектра всегда однозначно, т.е. для заданного сигнала можно определить один амплитудный спектр. Понятие фазового спектра свойством однозначности не обладает. Это связано с тем, что гармоническое колебание можно записать как в виде функции косинус, так и в виде функции синус (они, как известно, отличаются начальной фазой на π/2). Чтобы иметь однозначное определение фаз спектральных составляющих, условимся гармонический спектр сигнала всегда представлять в следующей форме:  Если же сигнал выражаем через ряд синусов, то необходимо заранее определять этот случай, а затем искать фазовый спектр. Графические изображения амплитудного и фазового спектров соответственно называют амплитудной и фазовой спектральными диаграммами. 1.4. Периодическая последовательность прямоугольных импульсов Периодическая функция состоит из импульсов прямоугольной формы АМ, длительностью τ и периодом повторения Т (Рис. 1.2). На участке  данная функция данная функция
 , ,где 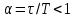 . .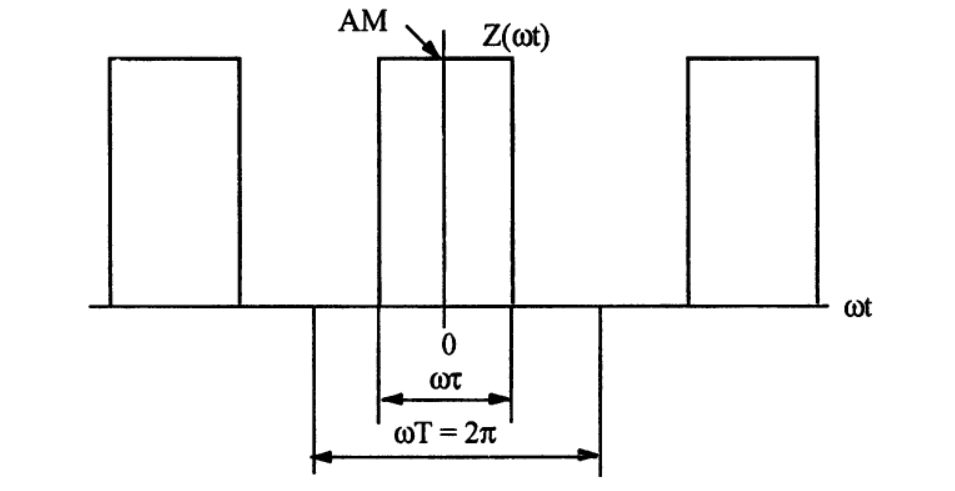 Рис. 1.2.  Рис. 1.3. Поскольку функция Z(ωt) четная, то синусные составляющие в разложении равны нулю. Программа на языке «Mathcad» по расчету постоянной составляющей 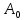 и амплитуд гармоник и амплитуд гармоник  приведена на рис. 1.3. В программе: приведена на рис. 1.3. В программе:  – число гармоник, – число гармоник,  – значение гармоники, выраженное в децибелах, относительно 1-й гармоники сигнала. Результаты расчета по программе при – значение гармоники, выраженное в децибелах, относительно 1-й гармоники сигнала. Результаты расчета по программе при 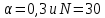 приведены на том же рис. 1.3. приведены на том же рис. 1.3. При прямоугольных импульсах спектральные составляющие можно вычислить также по формуле, взяв интеграл для коэффициента  в (1.5): в (1.5):
где   , , , , – круговая частота. – круговая частота.
Согласно (1.6) при  , где n – целое число, гармоники с круговой частотой , где n – целое число, гармоники с круговой частотой  или частотой или частотой  имеют значение амплитуды  . .Спектры, рассчитанные по программе (см. рис. 1.3) являются линейчатыми: спектральные составляющие в них следуют с интервалом  . Такой спектр для прямоугольных импульсов (см. рис. 1.2) при . Такой спектр для прямоугольных импульсов (см. рис. 1.2) при  , рассчитанный по программе (см. рис. 1.3), построен на рис.1.4. , рассчитанный по программе (см. рис. 1.3), построен на рис.1.4. Рис. 1.4 2. СПЕКТРАЛЬНЫЙ АНАЛИЗ ОДИНОЧНЫХ СИГНАЛОВ 2.1. Спектральный анализ непериодических сигналов Метод рядов Фурье допускает глубокое и плодотворное обобщение, позволяющее получать спектральные характеристики непериодических сигналов. Среди последних для радиотехники наибольший интерес представляют импульсные сигналы. Преобразование Фурье (Fourier transform) является инструментом спектрального анализа непериодических (импульсных) сигналов (их еще называют финитными, т.е. пространственно ограниченными). Такие сигналы отличны от нуля только на ограниченном интервале времени. Очевидно, что импульсный сигнал будет иметь и конечную энергию – если только он не содержит разрывов второго рода (с уходящими в бесконечность ветвями функции). Для иллюстрации перехода от ряда к интегральному преобразованию Фурье применяют не вполне строгий математически, но зато понятный аналитический подход. В теории спектрального представления непериодических импульсных сигналов используют искусственный прием, формально (мысленно) заменяя одиночные сигналы периодическими с бесконечно большим периодом следования 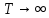 (Рис.2.1). Положим, что некая функция u(t) аналитически описывают одиночный импульсный сигнал конечной длительности (Рис. 2.1, а). Мысленно дополнив его такими же импульсными сигналами, следующими с некоторым интервалом Т (штриховые импульсы на рис. 2.1, б), получим периодическую последовательность аналогичных импульсов (Рис.2.1). Положим, что некая функция u(t) аналитически описывают одиночный импульсный сигнал конечной длительности (Рис. 2.1, а). Мысленно дополнив его такими же импульсными сигналами, следующими с некоторым интервалом Т (штриховые импульсы на рис. 2.1, б), получим периодическую последовательность аналогичных импульсов 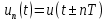 . . Рис. 2.1. Непериодические сигналы: а – одиночный импульс; б – условное периодическое представление Перейти от периодической функции к одиночному импульсу можно путем увеличения периода  . При этом промежутки между отдельными спектральными составляющими . При этом промежутки между отдельными спектральными составляющими  и спектр сигнала из линейчатого становится сплошным. Соответственно и дискретные значения частоты и спектр сигнала из линейчатого становится сплошным. Соответственно и дискретные значения частоты 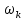 заменяются при этом на непрерывную величину ω, а сумма ряда – на интеграл. заменяются при этом на непрерывную величину ω, а сумма ряда – на интеграл.В результате ряд Фурье принимает вид интеграла
Входящая в (2.1) функция есть спектральная плоскость:
Интегралы (2.1) и (2.2) называются, соответственно, обратным и прямым преобразования Фурье. Одним из условий применяемости является абсолютная интегрируемость подынтегральной функции Φ(t) в (2.2). Подынтегральную функцию в (2.2) можно представить в виде:
Комплексная функция для спектральной плотности:
где
Амплитуда и фаза спектральной плотности:
Поясним физический смысл приведенных выражений прямого и обратного преобразований Фурье. Согласно (2.1) единичный импульс произвольной формы, описываемый вещественной функцией Φ(t), представляется бесконечной суммой синусоидальных колебаний. Сами эти колебания бесконечны малы по амплитуде и отличаются по частоте на бесконечно малую величину. Это отличие по частоте составляет dω, а амплитуда составляющей S(ω)dω, где S(ω) есть спектральная плотность размерность размерностью В/Гц. С ее помощью можно определить мощность сигнала при нагрузке в 1 Ом в интервале частотного спектра, заключенного в пределах от  : :
Приводимые ниже программы по определению спектральной плотности четырех видов единичных импульсов, составленные с помощью пакета программ Mathcad, имеютследующие общие черты: в их основе лежат выражения (2.5)-(2.7); длительность единичного импульса Φ(t) конечна и занимает интервал времени от 0 до τ или от –τ до τ, вне этого интервала  . Поэтому бесконечные пределы интегрирования в (2.5) – (2.6) заменяются на указанные величины; . Поэтому бесконечные пределы интегрирования в (2.5) – (2.6) заменяются на указанные величины;размерность величин при расчете. Если величина τ задана в секундах, то значения частоты f – в Гц, при τ – в миллисекундах f – кГц, при τ в микросекундах f – в МГц; значение спектральной плотности вычисляется в N точках частотной оси с шагом DF. Чем больше N и мельче шаг, тем выше точность, но и больше время счета. Обычно достаточно принять N=200…500. 2.2. Импульс прямоугольной формы Определим спектральное разложение для одного из простейших сигналов – прямоугольного импульса длительностью τ , имеющего единичную амплитуду (рис. 2.2).  Рис. 2.2. Одиночный прямоугольный импульс Выполняя прямое преобразование Фурье, получим
Последовательность прямоугольных импульсов, расстояние между спектральными линиями которой равно 1/T, спектр одиночного импульса сплошной. Спектр прямоугольного импульса изображен на рис.2.3. 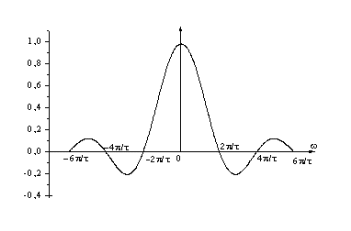 Рис. 2.3. Спектральное разложение прямоугольного импульса Определим теперь полуширину главного лепестка спектральной плотности (2.10а). Нетрудно видеть, что нули функции 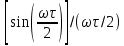 определяется значениями определяется значениями  , имеющими место при выполнении условия , имеющими место при выполнении условия  (k=1,2…). Тогда положение первого нуля спектральной функции, определяющее полуширину главного лепестка, можно найти из условия (k=1,2…). Тогда положение первого нуля спектральной функции, определяющее полуширину главного лепестка, можно найти из условия 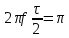 , ,откуда следует, что значение частоты, соответствующее первому нулю, определяется величиной 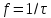 , обратно пропорциональной длительности импульса. Соотношение , обратно пропорциональной длительности импульса. Соотношение 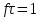 (или (или 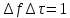 ) представляет собой принцип неопределенности. В соответствии с этим принципом протяженность сигнала по временной оси обратно пропорциональна протяженности спектра этого сигнала по оси частот. ) представляет собой принцип неопределенности. В соответствии с этим принципом протяженность сигнала по временной оси обратно пропорциональна протяженности спектра этого сигнала по оси частот.Рассмотрим теперь функцию времени x(t), которой соответствует спектральная плотность X (ω), равномерно распределенная на интервале 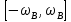 где где  частота – среза спектра. Вне указанного интервала спектральная функция X (ω) = 0 (рис. 2.4). частота – среза спектра. Вне указанного интервала спектральная функция X (ω) = 0 (рис. 2.4).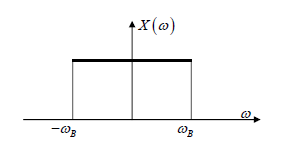 Рис. 2.4. Равномерная спектральная плотность Временная зависимость x(t), отвечающая заданной спектральной плотности X(ω), может быть найдена с использованием обратного преобразования Фурье  , ,где  есть половина ширины полосы частоты, ограниченной значениями есть половина ширины полосы частоты, ограниченной значениями 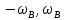 . Умножив и разделив последнее выражение на величину . Умножив и разделив последнее выражение на величину  , запишем результирующую форму функции x(t): , запишем результирующую форму функции x(t):
Перепишем здесь для удобства выражение (2.10а) 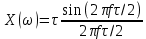 и сопоставим результаты (2.10а) и (2.10б). Сравнение этих выражений позволяет сформулировать принцип дуальности времени и частоты, заключающийся в следующем: Если функция X (ω) является преобразованием Фурье функции x(t), то функция x(−ω) есть преобразование Фурье функции X (t). Поскольку, в рассмотренных выше случаях, как функция времени, так и функция частоты являются четными и действительными функциями, то функция 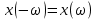 есть преобразование Фурье функции X(t). Это есть так называемый случай четной симметрии. есть преобразование Фурье функции X(t). Это есть так называемый случай четной симметрии.Программа по расчету спектральной плотности импульса прямоугольной формы (рис. 2.5) приведена на рис. 2.6. 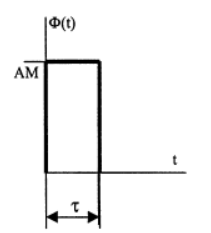 Рис. 2.5 На том же рис.2.6 построен график численной функции спектральной плотности при исходных данных, приведенных в начале программы. 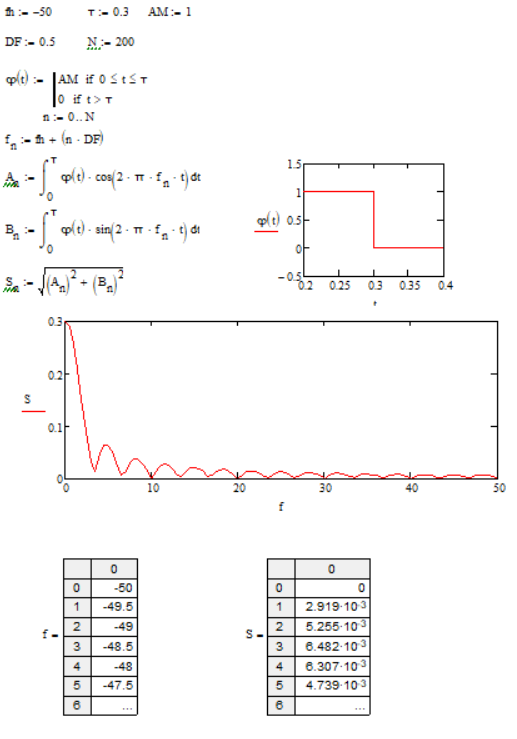 Рис. 2.6 Заключение В заключение данной работы были достигнуты следующие цели: закрепление на практике знаний, умений и навыков, полученных в процессе теоретического обучении; развитие навыков ведения самостоятельной практической работы, анализа и исследования научных данных; развитие способности по осуществлению анализа и обработки информации полученных из прикладных компьютерных программ, представления ее в требуемом формате с использованием информационных и компьютерных технологий; развитие готовности формировать презентации, научно-технические отчёты по результатам выполненной работы. Список литературы 1. Гоноровский, И. С. Радиотехнические цепи и сигналы. - М. : Дрофа, 2006. - 720 с. https://www.elec.ru/files/2020/02/13/_Gonorovsky_I.S.__Radiotehnicheskie_cepi_i_signalu.PDF 2. Баскаков, С. И. Радиотехнические цепи и сигналы. - М. : Высшая школа, 2004. - 464 с. http://www.naa.az/radioelectronics/wp-content/uploads/2019/10/1.%D0%91%D0%B0%D1%81%D0%BA%D0%B0%D0%BA%D0%BE%D0%B2-%D0%A1.%D0%98.-%D0%A0%D0%B0%D0%B4%D0%B8%D0%BE%D1%82%D0%B5%D1%85%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5-%D1%86%D0%B5%D0%BF%D0%B8-%D0%B8-%D1%81%D0%B8%D0%B3%D0%BD%D0%B0%D0%BB%D1%8B.pdf 3. Радиотехнические цепи и сигналы. Примеры и задачи : учебное пособие для вузов / Г. Г. Галустов, И. С. Гоноровский и др. / под ред. И. С. Гоноровского. - М. : Радио и связь, 1989. https://studizba.com/files/show/djvu/2259-1-gonorovskiy-i-s-radiotehnicheskie-cepi-i.html 4. Френке, Л. Теория сигналов: пер. с англ. / под ред. Д. Е. Вакмана. - М. : Сов. радио, 1974. http://www.radioscanner.ru/files/signals-analysis/file3711/ 5. Федосов, В. П., Нестеренко, А. К. Цифровая обработка сигналов в Lab VIEW / под ред. В. П. Федосова. - М. : ДМК-ПРЕСС, 2007. - 472 с. http://physicsbooks.narod.ru/Reference/Fedosov.pdf 6. Рудин У. Основы математического анализа 1976 https://obuchalka.org/2011062756865/osnovi-matematicheskogo-analiza-rudin-u.html 7. Пискунов Н. С. Дифференциальное и интергальное исчисления для ВТУЗов, т. 2. М., «Наука», 1964. 8. Нефедов. В.И. Основы радиоэлектроники и связи. М.: Высш. шк., 2002. 510 с. ISBN 5 – 06 – 004274 – Х. http://opac.hse.ru/absopac/app/webroot/index.php?url=/notices/index/IdNotice:240127/Source:default 9. В.Н. Татаринов, С.В. Татаринов СПЕКТРЫ И АНАЛИЗ https://edu.tusur.ru/publications/1490/download |




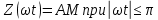 ,
,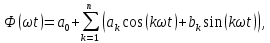

 .
. .
. .
. .
. ,
,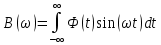 .
.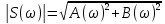 ,
, .
. .
.