Домашнее задание по термодинамике на тему Газовые смеси и теплоемкости. хз вообще. Газовые смеси и теплоёмкость
 Скачать 47.67 Kb. Скачать 47.67 Kb.
|
Газовые смеси и теплоёмкостьВ энергетических установках (ЭУ) в качестве теплоносителей выступают смеси газов (воздух, продукты сгорания топлив и пр.). Чистые вещества, составляющие смесь, называются её компонентами. Свойства смеси определяются свойствами отдельных компонентов и составом смеси. В качестве примера газовой смеси, которая может быть использована в качестве рабочего тела в замкнутых ЭУ, является смесь гелия и ксенона. Особенностью применения данной смеси является отсутствие химического взаимодействия её компонентов с элементами конструкции установки. Расчётное задание В объеме при давлении и температуре хранится смесь газа гелия He (атомная масса 4,003 а.е.м.) и ксенона Xe (атомная масса 131,3 а.е.м.). Состав смеси задан массовыми долями компонентов 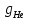 и и  . Исходные данные для расчёта приведены в таблице 1. . Исходные данные для расчёта приведены в таблице 1.Считая газы идеальными, определить: 1) относительный мольный (объёмный) состав смеси  , ,2) газовые постоянные компонентов и смеси  , ,3) среднюю молярную массу смеси , 4) парциальные давления 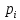 и парциальные объемы и парциальные объемы  компонентов, компонентов,5) плотности компонентов и смеси при нормальных условиях (  ) и при условиях хранения ( ) и при условиях хранения (  , ,6)парциальные плотности компонентов (т.е. плотности при  ), ),7) массу компонентов 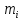 и смеси m; объем и смеси m; объем 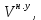 занимаемый смесью при нормальных условиях, занимаемый смесью при нормальных условиях,8) энтальпию, внутреннюю энергию и энтропию компонентов 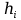 , ,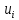 , , и смеси h,u,sпри условиях хранения, и смеси h,u,sпри условиях хранения,9) изобарную и изохорную истинные теплоемкости компонентов и смеси при условиях хранения: А) массовые Б) мольные В) объёмные (для 1 нм3, т.е. при нормальных условиях). Таблица 1. Исходные данные для расчёта.
Расчет 1.Определение относительного мольного (объёмного) состава смеси  . . Из определения  = =  . Так как . Так как 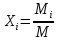  = =  , тогда , тогда 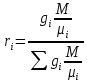 = =  Для исходных компонентов смеси получаем: 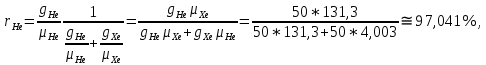  2.Расчёт газовых постоянных компонентов и смеси 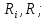 Из определения  получаем: получаем: 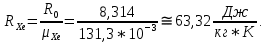 Определим газовую постоянную смеси, так как 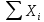 = X ⇔ = X ⇔ 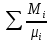 = = 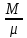 ⇔ ⇔ 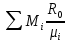 = = 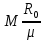 ⇔ ⇔ 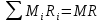 ⇔ ⇔ 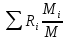 = R ⇔ = R ⇔ 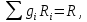 тогда для данной смеси получаем:  3.Определение средней молярной массы смеси. Имеем:  = = 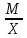 = = 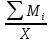 = = 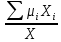 = =   = = 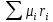 , тогда для данной смеси получаем: , тогда для данной смеси получаем: Для проверки воспользуемся значением газовой постоянной, полученной в пункте 2: 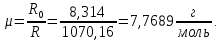 4.Определение парциальных давлений 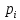 и парциальных объемов и парциальных объемов  компонентов. компонентов.Воспользуемся УСИГом  ⇒ ⇒  = =  = =  ⇒ ⇒  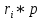 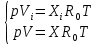 ⇒ ⇒ 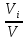 = =  = =  ⇒ ⇒ 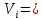 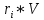 Для компонентов смеси получаем:  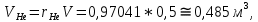  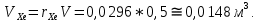 Проверка: 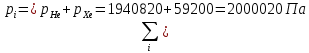 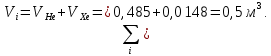 5. Плотности компонентов и смеси при нормальных условиях (  ) и при условиях хранения ( ) и при условиях хранения (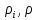 ); ); 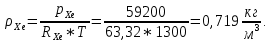  В качестве нормальных условий принимаются значения температуры и давления T=273,15 K и давления p = 101325 Па. Определим объём одного моля газа при НУ из УСИГ 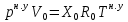 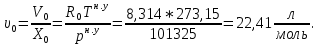 Тогда для компонентов и смеси получаем 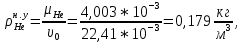  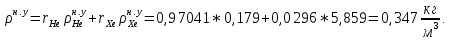 Проверка: 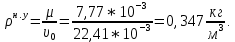 6. Парциальные плотности компонентов (т.е. плотности при  Из определения парциальной плотности компонента смеси получаем:  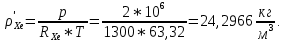 Проверка:  7.Определение массы компонентов 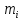 и смеси m; объем занимаемый смесью при нормальных условиях; и смеси m; объем занимаемый смесью при нормальных условиях;Из УСИГ получаем:  Из определения массовой доли следует, что  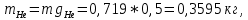  Проверка: Согласно соотношению m = Σ 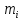 получаем: получаем: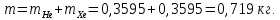 Запишем УСИГ для смеси при нормальных условиях  , откуда , откуда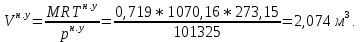 8. Расчёт энтальпии, внутренней энергии и энтропии компонентов 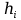 , , 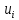 , ,  и смеси h , u, s при условиях хранения. и смеси h , u, s при условиях хранения.Из таблицы для T=1300 К =1026,85 ºC и при p=20 барнайдем значения h и s при p=20 бар : 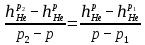 и и  . .
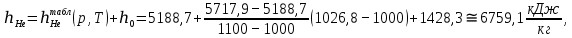   Из таблицы для T=1300 Ки при p=20 бар найдем значения h и s : 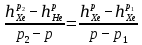 и и  . . 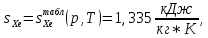 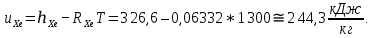 Для смеси:   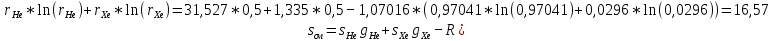  . .9. Определение изобарной и изохорной истинных теплоемкостей компонентов и смеси при условиях хранения. Из таблицы для Т=1300 К и р=20бар удельные изобарные теплоемкости: 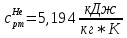 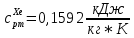 Из уравнения Майера для идеального газа находим удельные изохорные теплоемкости: 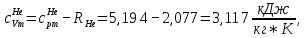  Удельная теплоемкость смеси в изобарном процессе:  Удельная теплоемкость газовой смеси в изохорном процессе:  Теперь переходим к нахождению истинных значений А)Массовые Из взаимосвязи истинной и удельной теплоемкостей в изобарном и изохорном процессе получаем:  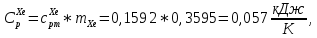 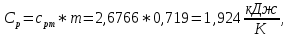 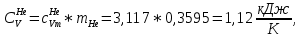  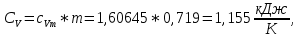 Проверка: 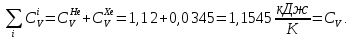 Б) Мольные. Из взаимосвязи удельной и мольной теплоёмкостей получаем: 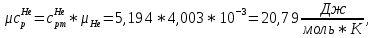 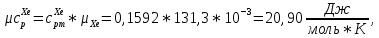  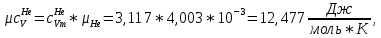   Проверка:  В) Объёмные при НУ. 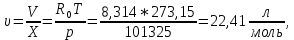 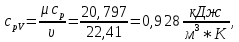 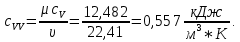 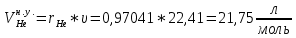  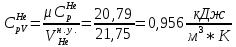 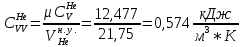   |

 ,
,