Сопромат. Геометрические характеристики поперечных

• Название: Геометрические характеристики поперечных
• Анкор: Сопромат
• Дата: 29.11.2021
• Размер: 255.44 Kb.
• Имя файла: sem_11.docx
• Тип: Документы; #285724

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ

При растяжении стержня напряжения во всех точках одинаковы, по- этому его напряженное состояние определяется внешней нагрузкой и пло- щадью поперечного сечения, но не зависит от его формы.

В случае изгиба и кручения брусьев напряжения в точках поперечно- го сечения зависят от его формы и размеров, а при изгибе еще и от его ориентации к направлению нагрузок. Кроме площади сечение характери- зуется:

статическим моментом площади; моментами инерции;

радиусами инерции; моментами сопротивления.

У большинства характеристик физического смысла нет, но есть гео- метрическая интерпретация и аналогия с физическими и механическими понятиями.
СТАТИЧЕСКИЙ МОМЕНТ ПЛОЩАДИ СЕЧЕНИЯ

_ydA

z

_AСтатическиймоментплощади– распро-страненная на всю площадь сумма произведений эле-ментарных площадок dA на расстояние от них доэтойоси

y
_z S_z _ yd 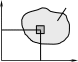A,

0 ^A

S_y _ zd A.

A

(6.1)

Рис. 6.1

Это понятие аналогично моменту силы относительно

оси. Если предположить, что А – вес пластины, имеющей форму нашего сечения, то статический момент S_z – это момент силы тяжести пластины относительно оси z.Размерность: единицы длины в третьей степени (см³;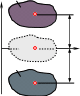

м³). Знаки: плюс, ноль и минус. _А

Осьцентральная– ось,относительно ^y

которойстатическиймоментплощадиравен ^C

нулю.

Центртяжестисечения–точкапере-

сеченияцентральныхосей. ^{0 C}

Если фигура имеет ось симметрии, то эта ^А

ось является центральной. _C

Статический момент составного сечения
y_C 0


y_C
S_z 0
y_C 0


y_C
^zS_z 0
y_C 0

S_z 0

равен сумме статических моментов элементов этого сечения. Это следует из свойства опреде- ленного интеграла, который можно вычислять по частям – свойство аддитивности (от англ.

Рис. 6.2. Связь знака стати- ческого момента площади с его положением в коор- динатной системе

add– прибавлять, присоединять, складывать). При известных статических

моментах частей сечения можно найти координаты центра тяжести состав- ной фигуры:

z  ^Sy

с <sub>A


</sub> z₁  A₁  z₂  A₂ ·  z_n A_{n ;}

A₁  A₂ · A_n
y_с ^Sz

A

_ y₁  A₁  y₂  A₂ · y_n A_n.

A₁  A₂ · A_n

МОМЕНТ ИНЕРЦИИ СЕЧЕНИЯ

Момент инерции – распространенная на всю площадь сумма про-изведений элементарных площадок dA на квадраты расстояний от них доэтойоси.

Осевыемоменты инерции

I_z _ y² d A,

A

I_y _ z² d A.

A

(6.2)

Полярныймомент инерции

I_p _ ρ² d A,

A

(6.3)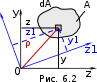

где ρ – расстояние от площадки dAдо точки


1
_y(полюса), относительно которого вычисляется полярный момент инерции. Полярный момент

инерции связан с осевыми моментами инерции


 ¹

1
I_p _ρ²  d A _ z²  y² d A z²  y² d A,

AAA

то есть для любой пары взаимно перпендику- лярных осей, проходящих через полюс 0

I_p I_z I_y I_z1  I_y1 . (6.4)

Центробежный момент инерции определяется интегралом произве- дений элементарных площадей на их расстояния до двух взаимно перпен- дикулярных осей

^Izy

 _ z y d A.

A

(6.5)

Размерность моментов инерции – единицы длины в четвертой степе- ни. Осевые и полярный момент инерции всегда положительны, центро- бежный момент инерции может принимать значения «+», «–» и ноль. Ес- ли фигура имеет ось симметрии, то относительно этой оси центробежный момент инерции равен нулю.

МОМЕНТ СОПРОТИВЛЕНИЯ

Моментсопротивления–отношениемоментаинерциикрасстоя-ниюдо наиболееудаленной точки.


^ymax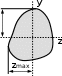
В расчетах на прочность при изгибе используют осевые моменты сопротивления

W_z

I_z

^ymax

и W<sub>y

</sub> I_y

^zmax

. (6.9)

Например, для прямоугольника

I bh³ 2

W_z^z 

bh²

,

I_y

W_y

_ b³h2

b²h



.

^ymax

12 h 6

^zmax

12 b 6

В расчетах на прочность при кручении сечений круглого профиля используют полярный момент сопротивления

W_p

I_p

^ρmax

. (6.10)

Так, для круга и кольца соответственно

_ I<sub>p

</sub> πD⁴

2. 
   _ πD³
   

_ I<sub>p

</sub> πD<sup>4

2</sup>  

⁴  ^πD3   ⁴ 

W_p

^ρmax


32 D

₁₆ . W_p

^ρmax

1 c

32 D

1 c .

16

Примечание. Для сечений некруглого профиля, например прямо- угольного, моменты инерции и моменты сопротивления вычисляют по специальным формулам, включающим высоту и ширину профиля, а также коэффициент, зависящий от отношения высоты к ширине.
ГЛАВНЫЕ ОСИ ИНЕРЦИИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

При изменении угла α значения I_z1, I_y1, I_z1y1 изменяются, и при некотором значении угла α₀ они принимают экстремальные значения. Взяв первую производную по углу α от формул и приравняв ее нулю, по- лучим:

tg 2α₀

 ^{ 2Izy}.

I_zI_y

Эта формула определяет положение двух осей, относительно одной из которых осевой момент максимален, а относительно другой – минима- лен. Такие оси называют главными.Моменты инерции относительно главных осей называют главными моментами инерции. Их вычис- ляют следующим образом:

^Imax,min ^

I_z I_y

2
.

Главные оси обладают следующими свойствами: центробежный момент инерции относительно них равен нулю; моменты инерции относительно главных осей экстремальны;

для симметричных сечений оси симметрии являются главными.

Главныеоси,проходящиечерезцентртяжестифигуры,называют

главнымицентральнымиосямиинерции.
Опоры и опорные реакции

Схемы реальных опорных устройств можно свести к трем типам.




Шарнирно-подвижнаяопорадопускает поворот опорного сечения и перемещение его в одном направлении. Опорная реакция перпендику- лярно к плоскости опирания катков.



Шарнирно-неподвижная опора допускает только поворот опорного сечения балки. Реакция имеет две составляющие: горизонтальную и верти- кальную.




Жесткая заделка (защемление) не допускает поворота опорного се- чения и любых его перемещений. Имеет три реакции: горизонтальную и вертикальную составляющие, а также опорный момент.

Построение эпюр внутренних усилий

Каждую из эпюр изгибающих моментов M_yи M_zпостроим в отдель- ности на растянутой части бруса (рис. П1.5, д, е). Эпюры крутящего мо- мента Ти осевого усилия Nцелесообразно совместить.

Сопоставив эпюры внутренних усилий, можно заключить, что опас- ными являются следующие сечения:

участок I – при x= 2a, плоский изгиб;

участок II – при x= a, совместное действие изгиба и кручения; участок III – имеет место изгиб в двух плоскостях, кручение и растя-

жение;

огибающие всех эпюр параллельны базисной линии – все сечения равно- опасны;
Минимальная площадь поперечного сечения:

Чтобы решить эту проблему, мы будем использовать общее соотношение для расчета сопротивления проводника по следующей формуле:
Сопротивление = Удельное сопротивление * (Длина / Площадь)
R = Сопротивление материала, Ом
Ρ = Удельное сопротивление материала, Ом на метр
L = Длина проводника, в метрах
A = Площадь поперечного сечения, в квадратных метрах
Чтобы использовать это общее соотношение для решения нашей примерной задачи, нам требуется удельное сопротивление или удельное сопротивление меди.Обратите внимание, что мы получаем удельное сопротивление материалов проводников из таблицы удельных сопротивлений проводников, и теперь мы знаем, что удельное сопротивление меди составляет 1,72 x 10e-8 Ом на метр.
При вычислении сопротивления проводника не забудьте выразить сопротивление в омах, удельное сопротивление материала в омах на метр, длину проводника в метрах и площадь поперечного сечения в квадратных метрах, чтобы это соотношение было действительным. Затем мы можем перейти к вычислению площади поперечного сечения провода, подставив известные величины в примере.
A = Ур. (1)

Расчет минимальной площади поперечного сечения бруса