План урока. Геометрические построения
 Скачать 6.27 Mb. Скачать 6.27 Mb.
|
|
ГБПОУ «Троицкий технологический техникум»
Предмет: инженерная графика Тема: Геометрические построения. Деление отрезков, углов, окружностей на равные части. г. Троицк, 2019 год Технологическая карта занятия
Урок: Геометрические построения. Деление отрезков, углов, окружностей на равные части Этапы урока: - постановка цели урока и мотивация учебной деятельности; - воспроизведение и коррекция опорных знаний; - изложение нового материала; - практическая работа; - подведение итогов урока; - домашнее задание. Методы: - информационный (словесный); - наглядный; - иллюстративный; - репродуктивный (индивидуальная практическая работа). Межпредметные связи: - техническая механика; - материалы и изделия; - особенности проектирования в автомобиле и тракторостроении; - организация и контроль работ по эксплуатации автомобилей и тракторов. Формы организации учебной деятельности: фронтальная, индивидуальная. Ход урока. 1. Организационный момент. 2. Приветствует учащихся, наблюдает за готовностью к уроку каждого обучающегося - Здравствуйте. Записываем тему нашего занятия: «Геометрические построения. Деление отрезков, углов, окружностей на равные части», а я проверю отсутствующих. 3. Постановка цели и задач урока, повторение правил и выработка практических навыков в делении отрезков и окружностей на равные части. Ставится цель и задачи перед обучающимися: повторить, закрепить и углубить знания о выполнении геометрических построений. 4. Мотивация. Некоторые детали машин и приборов имеют элементы, равномерно расположенные по окружности, например, такие детали как: крышка, фланец, плашка, звездочка, шкив и др. При выполнении чертежей подобных деталей необходимо знать правила деления окружности на равное количество частей. На сегодняшнем занятии из многочисленных построений, которые встречаются при выполнении чертежей, мы рассмотрим самые распространенные. 5. Повторение и проверка знаний: - Давайте с Вами вспомним, что мы узнали на прошлых занятиях. Вопрос 1. Какой линией мы чертим основную рамку, надпись и видимый контур детали? Ответ – Сплошная толстая основная Вопрос 2. А какая толщина у этой линии? Ответ – 1мм Вопрос 3. Какой линией мы чертим осевые и центровые? Ответ – Штрихпунктирная тонкая Вопрос 4. Какая толщина этой линии? Ответ – 0,5 мм Вопрос 5. Какой номер шрифта мы применяем на чертеже, когда ставим размеры? Ответ – Шрифт №5 Вопрос 6. Скажите уклон шрифта? Ответ - 75° Вопрос 7. В каких единицах измерения проставляют размеры на чертеже? Ответ – В мм. 6. Изучение нового материала. При выполнении чертежей деталей приходится делить на равные части отрезки прямой линии, углы, окружности и их дуги. Рассмотрим, как это сделать. (Приложение 1 – Презентация) Сейчас берем линейку и карандаш и делим свою тетрадь по схеме, которую я вам начерчу на доске (рис.1)  Рис. 1 Рис. 1 В верхней части листа слева начертите отрезок 50мм. Мы разделим его на 2 и 4 равные части с помощью геометрических построений (рис. 2).  Рис. 2 Рис. 2Чтобы разделить отрезок прямой пополам, из его концов проводим дуги радиусом больше половины длины этого отрезка. Точки пересечения дуг соединяем прямой линией, которая делит отрезок прямой на две равные части (АВ=ВБ) и является перпендикуляром к нему. На четыре равные части отрезок прямой можно разделить аналогично: вначале делим отрезок АБ пополам, а затем каждую половину АВ и ВБ – еще раз пополам, где радиус больше половины этих отрезков. Так можно делить на любое число равных частей, кратное четырем. А как же на 3, 5, 6, 7 …, п частей? Посмотрите на рис.3: отрезок АБ разделен на 9 равных частей.  Рис. 3 Рис. 3Выполняется это так: - проводим луч АВ под произвольным углом к АБ; - откладываем на луче АВ от точки А нужное количество (п) равных отрезков произвольной длины; - соединяем последнюю точку п (9)с точкой Б; - из каждой точки на луче АВ (1, 2, 3, …, п) проводим прямые, параллельные отрезку 9Б, и получаем на АБ требуемое количество равных частей. Необходимо уметь делить окружность на равные части и строить правильные многоугольники. Любой диаметр делит окружность на 2 равные части. Для нахождения точек, делящих окружность радиуса Rна 3 равные части, достаточно из любой точки окружности, например, точки В, провести дугу радиусом R. Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет находиться на пересечении оси окружности, проведенной из точки А, с окружностью (рис. 4).  Рис. 4 Рис. 4Разделить окружность на 3 части можно также угольником с углами 30° и 60° (рис. 5). Гипотенуза угольника должна проходить через центр окружности. 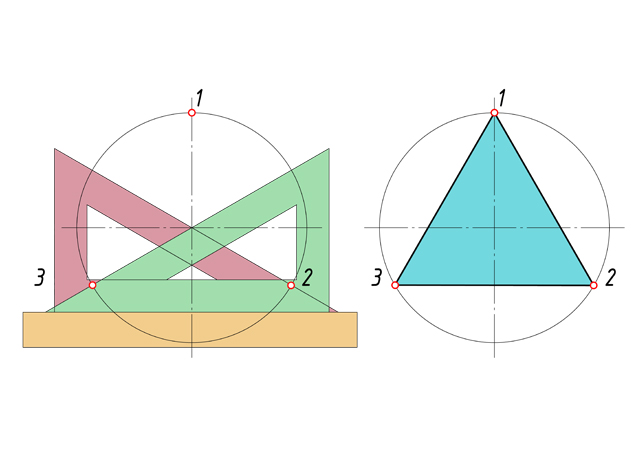 Рис. 5 Рис. 5Чтобы разделить окружность на 4 части применяют прием деления прямого угла с помощью циркуля на две равные части (рис. 6). Из точек пересечения дуги окружности со сторонами угла (точки А и С) проводим две пересекающиеся дуги радиуса равного радиусу окружности. Точку их пересечения соединяем с вершиной угла D. Угол АDС и дуга АС разделились пополам. Аналогично делим и угол СDВ. Соединив последовательно все точки, получим квадрат.  Рис.6 Рис.6Разделить окружность на 4 части можно с помощью угольника 45° (рис. 7). Гипотенуза угольника должна проходить через центр окружности. 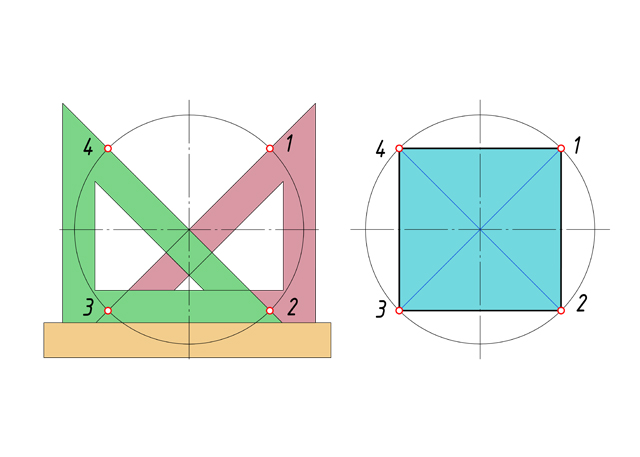 Рис.7 Рис.7Чтобы разделить окружность на 4 равные части, нужно провести два взаимно перпендикулярных диаметра окружности (13, 24). Тоже самое можно выполнить с помощью угольника 45°. Гипотенуза угольника должна проходить через точки пересечения центровых линий и окружности (рис. 8). 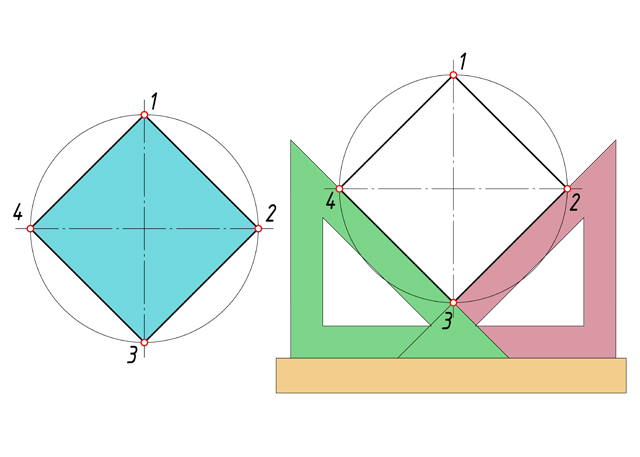 Рис. 8 Рис. 8Деление окружности на 5 равных частей начинаем с проведения из точки А радиусом окружности Rдуги, которая пересекает окружность в двух точках (рис. 9). Соединив точки пересечения прямой, при пересечении с горизонтальной осевой линией получаем точку В. Из точки В, радиусом равным отрезку ВС, проводим дугу, которая пересечет горизонтальную осевую линию в точке D. Соединив точки С и Dполучаем отрезок СD, который и является 1/5 длины окружности. Из тоски С проводим дугу радиусом равным СD и получаем точки 5 и 2. Из полученных точек проводим еще по одной дуге и находим точки 3 и 4.  Рис. 9 Рис. 9На рис.10 показано деление окружности циркулем на 6 равных частей. В этом случае выполняется то же построение, что и при делении окружности на 3 части, но дугу описывают не один, а два раза, из точек 1 и 4 радиусом окружности R. 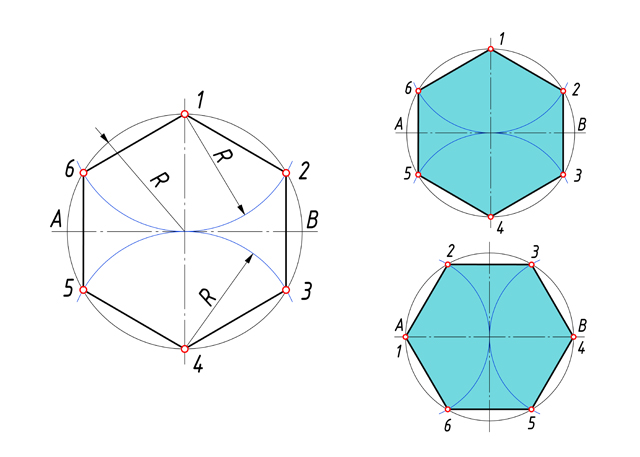 Рис. 10 Рис. 10Разделить окружность на 6 равных частей можно и при помощи угольника с углами 30° и 60° (рис. 11). Гипотенуза угольника должна проходить через центр окружности. 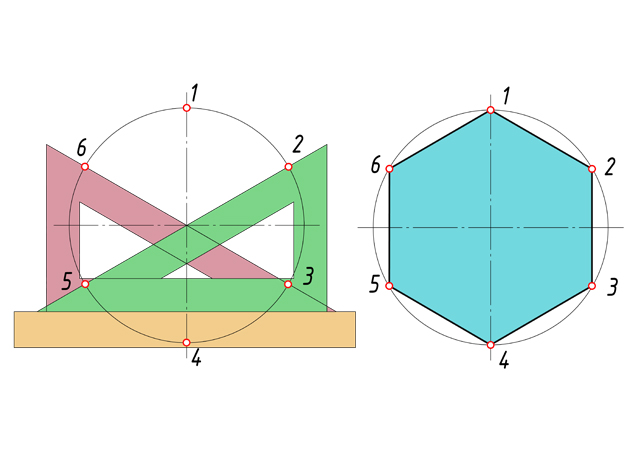 Рис. 11 Рис. 11Разделим окружность на 7 равных частей (рис. 12). Из точки А проводим дугу радиусом окружности R, которая пересекает окружность в двух точках. Соединив точки пересечения прямой, при пересечении с горизонтальной осевой линией получаем точку В. Из точки 1 радиусом, равным отрезку СВ, делают по окружности 7 засечек и получают семь искомых точек.  Рис. 12 Рис. 12 Чтобы разделить окружность на 8 равных частей, достаточно провести две пары диаметров, т.е. объединить оба случая построения квадрата (рис. 13). Это построение два взаимно перпендикулярных диаметра окружности и прием деления прямого угла с помощью циркуля на две равные части. 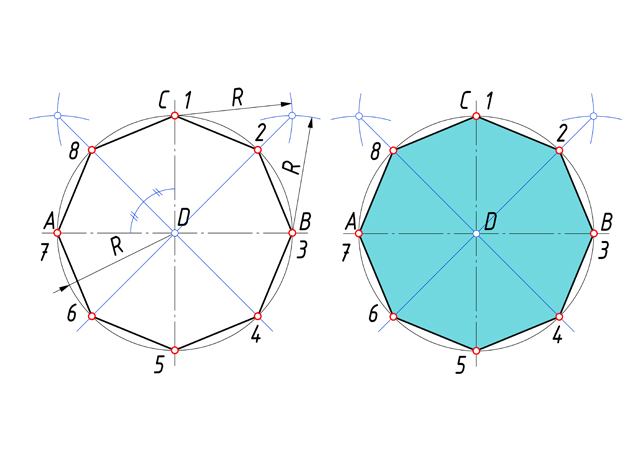 Рис. 13 Рис. 13Деление окружности на 9 равных частей начинаем с проведения из точки А радиусом окружности Rдуги (рис. 14). Из точки С построим вторую дугу радиусом равным отрезку СD, которая пересекает горизонтальную ось окружности в точке Е. Соединив точку пересечения двух дуг F и точку Е, получаем отрезок равный 1/9 длины окружности. Из точки 1 радиусом, равным отрезку FЕ, делают по окружности 9 засечек и получают девять искомых точек.  Рис. 14 Рис. 14Чтобы разделить окружность на 10 равных частей, нужно сначала разделить ее на 5 равных частей (рис. 15). Отрезок ЕD является стороной десятиугольника. Из точки 1 радиусом, равным отрезку ЕD, делают по окружности 10 засечек и получают десять искомых точек.  Рис. 15 Рис. 15При делении окружности на 12 равных частей с помощью циркуля используют тот же прием, что и при делении окружности на 6 равных частей (рис. 16), но дуги радиусом окружности R описывать 4 раза из точек 1, 4, 7, 10.  Рис. 16 Рис. 16Используя угольник с углами 30° и 60° с последующим поворотом на 180°, делят окружность на 12 равных частей (рис.17).  Рис.17 Рис.17С достаточной точностью можно делить окружность на число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (рис.18). 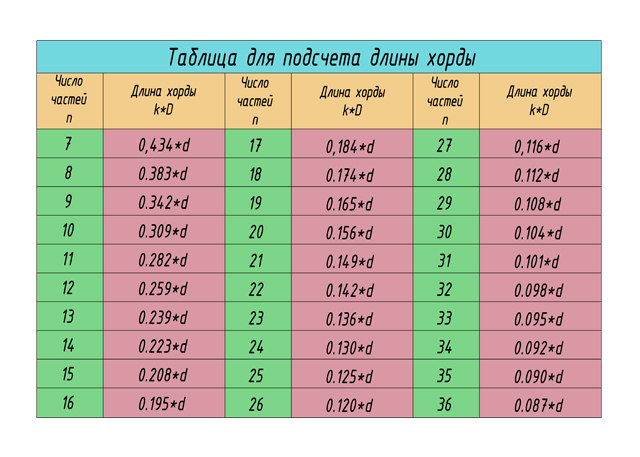 Рис. 18 Рис. 18Зная, на какое число (п) следует разделить окружность, находят по таблице коэффициент k. При умножении коэффициента k на диаметр окружности D получают длину хорды l, которую циркулем откладывают на окружности п раз (рис. 19).  Рис. 19 Рис. 197. Подведение итогов урока. Рефлексия. 8. Домашнее задание. Раздаю карточки на построение деталей с делением окружности на равные части (Приложение 2). Приложение 1    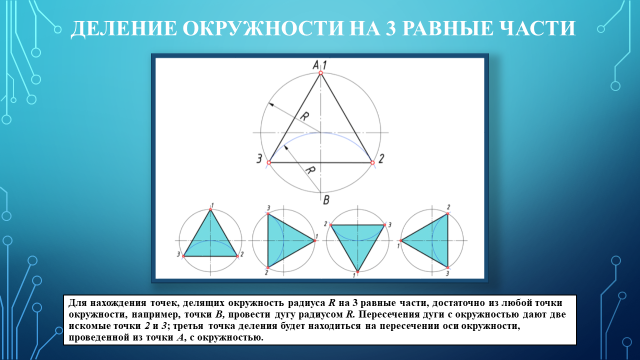      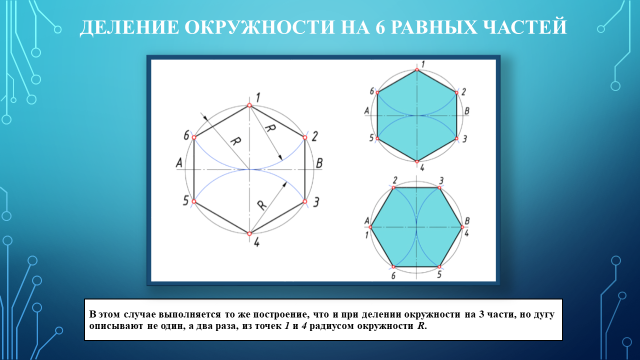 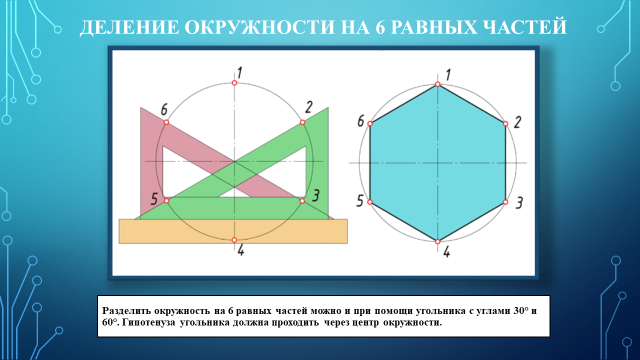         П  риложение 2 риложение 2  |
