Геометрия. Геометрия измерительных инструментов
 Скачать 1.39 Mb. Скачать 1.39 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ШКОЛА № 2 РЕФЕРАТ НА ТЕМУ: «ГЕОМЕТРИЯ ИЗМЕРИТЕЛЬНЫХ ИНСТРУМЕНТОВ»  Подготовила: ученица 10 Б кл. ЛЕБЕДЕВА ВИКТОРИЯ АНДРЕЕВНА Руководитель: МОСЕНКОВА ЛЮБОВЬ АНАТОЛЬЕВНА г. ВЯЗЬМА 2007 год План Введение………………………………………………………….3 Геометрия измерительных приборов Верёвка и трость…………………………………………..4 Шаблоны……………………………………………………5 Солнышко и карта...……………………………………….9 Бороздомер………………………………………………..11 Нониус…………………………………………………….12 Нивелир……………………………………………………13 Эклимер……………………………………………………14 Угломеры……………………………………………….....15 Откосные лекала…………………………………………..16 Центроискатели……………………………………………17 Мерный циркуль…………………………………………..18 Высотомеры………………………………………………..19 Молокомер…………………………………………………20 Наездник……………………………………………………21 Сферометр………………………………………………….22 Заключение………………………………………………………..24 Используемая литература………………………………………...25 Введение Геометрия – одна из самых древних наук, она возникла очень давно, ещё до нашей эры. В переводе с греческого слово «геометрия» означает «землемерие» («гео» - по-гречески земля, а «метрео» - мерит). Такое название объясняется тем, что зарождение геометрии было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, проведении дорог, строительстве зданий и других сооружений. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениям. Таким образом, геометрия возникла на основе практической деятельности людей и в начале своего развития служила преимущественно практическим целям. В дальнейшем геометрия сформировалась как самостоятельная наука. Многие изучаемые в школе теоремы и приемы геометрии положены в основу конструкции или способов использования различных измерительных приборов. Демонстрация таких приборов и выяснение их геометрической сути – впечатляющие примеры полезности математических знаний. Некоторые приборы и инструменты описаны в школьных учебниках. Например, у Л.С. Атанасяна упоминаются экер, рейсшина, малка, уголковый отражатель, рейсмус и др. Такие приборы можно подобрать для применения как содержательных геометрических теорем, так и самых первоначальных сведений из геометрии. При этом необязательно демонстрировать приборы фабричного изготовления (см., например, рис. 10 а, 16 а, 21 б – фотографии). Достаточно показать бесхитростные модели – на них лучше видна геометрическая суть – или даже ограничиться рисунками. Практически все измерительные инструменты используют прием косвенных измерений, когда интересующую величину измерить невозможно или затруднительно. Измеряют доступные величины, через которые искомые выражаются по каким-то формулам. Некоторые примеры таких измерений – высота предмета, недоступные расстояния – рассматриваются во всех школьных учебниках геометрии. ОСНОВНАЯ ЧАСТЬ Веревка и трость Величина угла на местности часто определяется линейными промерами. На сторонах угла откладывают отрезки (рис. 1) АВ = АС = 10 м и измеряют ВС. Какова величина угла, если ВС = а м? Решение. Если 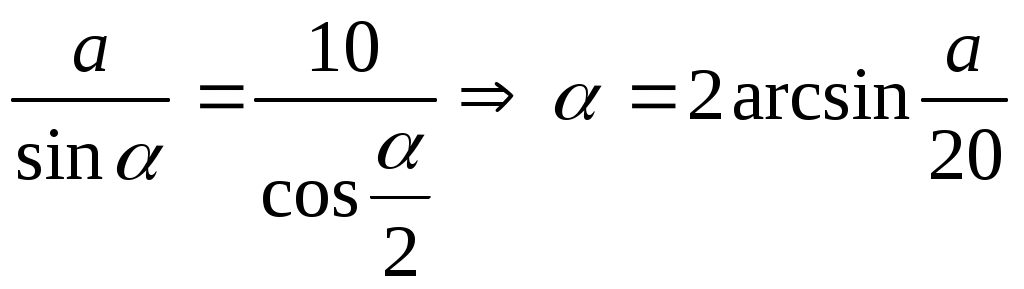 . Искомый угол теперь можно найти по таблицам значений синуса или с помощью микрокалькулятора. . Искомый угол теперь можно найти по таблицам значений синуса или с помощью микрокалькулятора.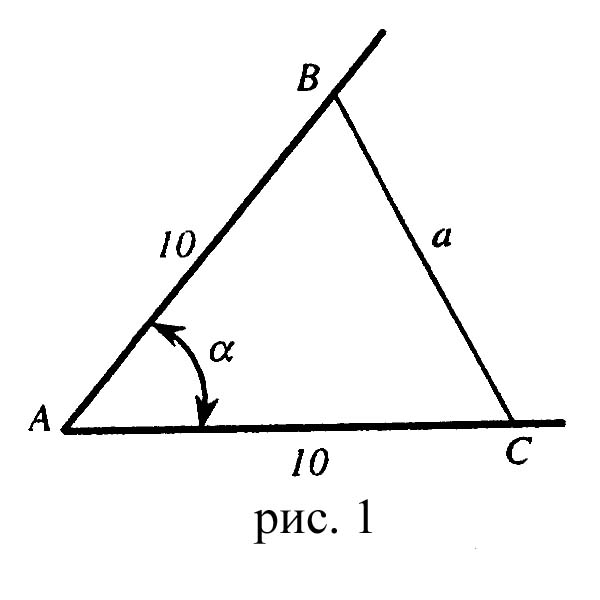 Шаблоны На рисунке 2а изображен разрез цилиндрической детали. Как с помощью кронциркуля и линейки определить внутренний диаметр цилиндра? Решение Кронциркуль с произвольным раствором h устанавливаем так, как показано на рисунке 2 б, и по линейке считываем величину b . Теперь имеем: d = D – 2 (h – b).  Определение угла конического углубления на практике обычно производится (см. примечание) с помощью двух шаров радиусов r и R (рис 3). Чему равен угол Решение. Рассмотрим осевое сечение конуса АОВ. Центры шаров Sи Pлежат на биссектрисе углаAOB. Проведём прямую ST, параллельную АО. Тогда TP Технические измерения. Источник задач рисунки 3, 5а.  Широко распространённые профили «ласточкин хвост» (рис. 4 Решение. Пусть E - точка касания одного из роликов и прямой BC. Так как точка O(центр окружности) лежит на биссектрисе угла C, то Поэтому СЕ = ОЕ · ctg 27°30´ = 1,921 Поскольку BC = 2 · CE + d + a, то a = b–2,921 d.  Величины углов в трапецеидальном пазе определяются с помощью четырёх одинаковых роликов (рис. 5 а). Найти величины углов, зная величины m Решение. Пусть А и В - точки пересечения оси симметрии трапеции с линиями центров верхних и нижних роликов, АС - прямая, параллельная боковой стороне трапеции (рис. 5 б). Получили прямоугольный треугольник АВС, в котором, каклегко показать, АВ = h, BC =  На рисунке 6 изображено осевое сечение болта с так называемой метрической резьбой. Профиль такой резьбы представляет собой правильные треугольники (S При контроле нарезаемой резьбы средний диаметр измеряют методом трёх проволочек: во впадины резьбы вкладывают одинаковые цилиндрические калибры - проволочки (для ориентации оси измерений в направлении, перпендикулярном оси резьбы) и находят размер М. Затем d гдеd- диаметр проволочек, P = S Решение. Так как DE - половина шага резьбы, то EC =P/4. Поэтому из треугольника DCE находим, что Пусть F- точка касания окружности (сечения проволочки) и профиля резьбы. Тогда из прямоугольного треугольника FBDнаходим, что BD=2BF=d. Значит, d откуда и следует, что d  Солнышко и карта Впервые длину радиуса Земли нашел древнегреческий ученый Эратосфен. Он узнал: когда в городе А солнце находится в зените, в городе В, находящемся с А на одном меридиане, солнечные лучи образуют с отвесной прямой угол величины α = 7º12´ (рис. 7). Оценив по времени движения каравана расстояние от А до В (800 км), он вычислил радиус Земли. Какое значение у него получилось? Решение. Так как прямые SА и SВ (лучи солнца) параллельны, то величины углов АОВ и SВР равны, а потому из формулы для длины дуги окружности находим: R  На топографических картах изображают не только плановое положение объектов местности, но и рельеф. Рельеф изображается горизонталями – замкнутыми кривыми линиями, проходящими через точки земной поверхности с одинаковой высотой (рис. 8 а). Разность высот двух соседних горизонталей h постоянна для данной карты, она называется высотой сечения рельефа. Горизонталями изображаются только плавные по форме склоны, более крутые участки изображаются специальными знаками. Для определения крутизны линий (например, участка дороги АВ) на картах за рамкой печатается специальный график (рис. 8 б). Отложив на оси абсцисс отрезок ab, на оси ординат прочитаем крутизну отрезка АВ на местности. Указать функцию, график которой изображен на рисунке, если известно, что он скопирован с карты масштабом 1:50 000 при высоте сечения рельефа h = 10 м. Решение. Отрезок ab – горизонтальная проекция участка дороги АВ. Проведем через АВ вертикальную плоскость, а в этой плоскости – горизонтальную прямую АС и вертикальную прямую ВС. Получим треугольник АВС (рис. 8в), в котором ВАС – искомый угол у, АС = ab = 50000х, ВС = h = 10000 мм. Отсюда находим, что у = arcctg На рисунке изображен график этой функции (со своеобразным масштабом на оси ординат). Для отрезка АВ по графику находим крутизну в 2º. То же значение получаем и по формуле у = arcctg5·6.   Бороздомер Рассмотрим инструмент (рис.9 а), с помощью которого удобно производить проверку глубины вспашки. Он состоит из двух линеек одинаковой длины: неподвижной, оканчивающейся угольником, и подвижной. Для замера глубины пахоты бороздомер устанавливают вертикально угольником на непаханую поверхность поля, а подвижную линейку опускают на расчищенное дно борозды. Верхний конец подвижной линейки показывает глубину борозды по шкале, нанесенной от верхнего конца неподвижной линейки. Доказать это. Доказательство. С геометрической точки зрения нам дан отрезок АD ( рис. 9 б) и точки В и С на нем, причем известно, что АС = ВD. Требуется доказать, что СD = АВ. На основании свойства измерения отрезков можно записать, что АС = АВ + ВС, ВD = ВС + СD. Так как АС = ВD, то АВ + ВС = ВС + СD. Отсюда и следует, что СD = АВ.  Нониус Для увеличения точности измерения отрезка во многих приборах (см., например, штангенциркуль на рис. 10 а) используется специальное приспособление – нониус. Нониус представляет собой вспомогательную линейку n (рис. 10 б) длиной в 9 единиц шкалы основной линейки m, разделенную на 10 равных частей. Если конец измеряемого отрезка АВ не совпадает с делением основной линейки, то к концу его приставляют нониус и смотрят, какое деление нониуса совпадает с делением основной линейки. В ситуации, изображенной на рисунке 10 б, полагают, что АВ = 5,6 ед. Доказать, что это действительно так. Доказательство. Так как одно деление нониуса равно 0,9 ед. основной линейки, то в нашем случае имеем: АВ + 6·0,9 = 11. Отсюда и следует, АВ = 5,6 ед.  Нивелир На рис. 11 изображен нивелир, который с помощью зрительной трубки и уровня позволяет проложить горизонтальный луч визирования между двумя рейками с делениями для определения превышения h точки В земной поверхности над точкой А. Доказать, что h = a – b. Доказательство. Так как рейки вертикальны, то h – искомое превышение, а поскольку луч визирования горизонтален, то изображенный на рисунке четырехугольник – параллелограмм. Значит, a = b + h.  Эклиметр Рассмотрим модель эклиметра – прибора для измерения на местности величины угла наклона прямой OS (см. рис.12; ОР – нить с грузиком). Доказать, что нить ОР показывает на шкале величину искомого угла. Доказательство. Угол наклона прямой – это угол, который она образует с горизонтальной прямой. Нить с грузиком – отвес – занимает положение прямой, перпендикулярной горизонтальной прямой. Проведя из точки О перпендикуляр к прямой SО, получим угол РОВ, величину которого показывает шкала прибора. Так как треугольник ОРS прямоугольный, то Поэтому Замечание. Мы решили задачу в предположении, что в принятом учителем школьном учебнике (как, например, у Погорелова) нет теоремы об углах с взаимно перпендикулярными сторонами. Ясно, что суть здесь в этой теореме.  Угломеры На рисунках 13 а и 13 б изображены модели угломера с отвесом (вокруг центра шкалы вращается стрелка с шариком) и угломер с поворотным шаблоном (вокруг вершины вращается прямой угол), предназначенные для контроля инструментов (резцы, сверла, фрезы, зенкеры и т.д.). На каких теоремах основан принцип действия этих приборов? Решение. Прямая а, проходящая через центр прибора и нулевое показание шкалы, параллельна основанию прибора b, так как при нормальном положении прибора (на горизонтальной плоскости) прямые а и b были горизонтальны. Значит, на рисунке 13а работает теорема об углах с соответственно параллельными сторонами. На рисунке 13 б при измерении угла  Откосные лекала При отсыпке насыпи правильность заложения откосов проверяется при помощи откосных лекал. Откосное лекало изготовляют из досок в форме прямоугольного треугольника (рис. 14 а) с удлиненной гипотенузой, один из острых углов которого равен углу наклона откоса. Приложив гипотенузу треугольника к отсыпанному откосу, в положительном случае получим, что отвес, закрепленный в точке А, совпадет с катетом. На каких теоремах геометрии основан принцип действия откосного лекала? Решение. Пусть СD (рис. 14 б) – горизонтальная прямая. Угол заложения откоса ВС – это угол ВСD. Ему равен, в силу конструкции треугольника, угол В. У нас получилось, что при пересечении двух прямых секущей накрест лежащие углы равны. Значит, по признаку параллельности двух прямых прямые АВ и СD параллельны. Так как АС  Центроискатели Для закрепления цилиндрической детали в токарном станке необходимо отметить центр круглого основания. Для этой цели используются так называемые центроискатели. Вот два из них (рис.15 а), АВ – серединный перпендикуляр к отрезку СD; рис. 15 б, АВ – биссектриса угла САD). Выбрав два положения центроискателя (положение ясно из рисунков) и проведя след по прямой АВ, мы в пересечении этих следов и получим центр окружности. Доказать, что с помощью центроискателей описанным выше способом действительно можно найти центр окружности. Доказательство. Описанный способ действия представляет собой построение точки (центра окружности) методом геометрических мест. Поэтому нам достаточно доказать, что 1) серединный перпендикуляр к хорде проходит через центр окружности; 2) биссектриса угла проходит через центр окружности, вписанной в этот угол. Первое утверждение вытекает из теоремы о серединном перпендикуляре, так как концы хорды С и D равноудалены от центра окружности. Для доказательства второго утверждения соединим центр окружности с точками касания Е и F и рассмотрим прямоугольные треугольники ОЕА и ОFА. Они равны по гипотенузе и катету. Отсюда и следует, что ОА – биссектриса.  М  ерный циркуль ерный циркульНа рисунке 16 а (фотография) изображен мерный циркуль, используемый для измерения различных частей тела животного. Шкала циркуля устроена так, что в зависимости от величины х угла АОВ ( а) Найти формулу для градуирования шкалы циркуля (зависимость lот х). Решение. Из прямоугольного треугольника АСО (рис. 16 б) имеем АС = АО · sin l= 2 r sin б) У мерного циркуля фабричного изготовления r = 44 см угол между кромками m и n в сомкнутом состоянии равен 50º. Какова максимальная величина, которую можно измерить этим циркулем? Решение. Предельный случай измерения, когда кромки m и n образуют развернутый угол. При этом Шкала фабричного прибора проградуирована до 75 см. На фотографии она, к сожалению, не видна. Высотомеры На рисунке 17 изображен высотомер лесника. Он представляет собой прямоугольную пластинку размером 10х10 см с закрепленным в точке А отвесом, шкалой на стороне ВС и визирами в точках А и D. Наведя с помощью визиров сторону АD на вершину дерева Е и заметив деление шкалы, которое показывает отвес АF, лесник с помощью несложной формулы и находит высоту дерева. Пусть, например, ВF = 3 см. Докажите, что Н = h Доказательство. Пусть tg  На рисунке 18 а изображен так называемый маятниковый высотомер (1 – визирующая трубка, 2 – подвижный маятник, находящийся при работе в вертикальном положении). На рисунке 18 б изображена схема использования высотомера. Чтобы определить высоту дерева, следует стать от него на расстоянии 10 м и навести визирующую трубку на его вершину. По основной (верхней) шкале прибора снимается показание, к которому прибавляется высота до глаза наблюдателя. Вывести формулы для градуирования шкалы прибора. Решение. Пусть  Молокомер Для измерения небольших объемов молока используется молокомер. Он представляет собой (рис.19) цилиндрическое ведро с поплавком, к которому прикреплена мерная шкала. Крупные деления на шкале соответствуют литрам. Внутренний диаметр стандартного молокомера – 21 см. Чему равно расстояние между крупными делениями шкалы? Решение. Искомое расстояние h равно высоте цилиндра, диаметр которого 21 см, а объем – 1 л. Поэтому h =  Наездник Для измерения радиуса R большого цилиндра используется накладной прибор – наездник, который представляет собой тележку (см.рис.20) с подвижным вертикальным стержнем l , фиксированная точка А которого (индикатор) при расположении наездника на горизонтальной прямой а находится в положении точки В – на одном уровне с центрами колесиков наездника, а при нахождении на окружности Решение. Так как СО = R + r, СВ = l , ОВ = R + r – h, то положив m = R + r, по теореме Пифагора получаем: Мы рассмотрели случай измерения с помощью наездника наружного диаметра цилиндра.  При измерении с помощью наездника внутреннего диаметра цилиндра индикатор по сравнению с положением на прямой опускается на величину h. Если выразить R через r, h и l, то в этом случае: R = Сферометр Имеется сегмент некоторого шара (например, линза). Требуется определить радиус соответствующего шара. Это делают с помощью сферометра, который представляет собой полый цилиндр с подвижной осью. Найти радиус шара R, если известен радиус основания цилиндра а, а ось цилиндра после его установки на шаровую поверхность (см. рис. 21 а) выдвинулась на величину h. Решение. Пусть О – центр шара (на рисунке отсутствует). Тогда ОЕ = ОС = R, АВ = СD = h , DЕ = а. Искомую зависимость найдем по теореме Пифагора из треугольника ОDЕ. Ответ: R = По этой формуле можно проградуировать шкалу прибора, и тогда он будет показывать искомую величину без дополнительных вычислений (см. рис. 21 б – фотография такого прибора).  ЗАКЛЮЧЕНИЕ Мне было интересно работать над выбранной темой. Она меня заинтересовала своей простотой. А всё простое, как известно гениально. С измерительными инструментами мы постоянно встречаемся в повседневной жизни, а наши родители на производстве. Во время сельскохозяйственных работ в поле, постоянно необходимо проводит контроль глубины пахоты. Для этого используют бороздомер. Ведь качественная заделка семян это основа будущего урожая. Токари во время своей работы постоянно пользуются кронциркулем, угломером штангенциркулем, да и в быту эти инструменты бывают достаточно часто необходимы. Мерный циркуль – инструмент без которого не могут обойтись в своей работе акушеры. Во многом благодаря полученным измерениям врачи могут прогнозировать течение родов и здоровье новорождённого. Все эти казалось бы нематематические знания я смогла получить на уроках геометрии, изучая измерительные инструменты. Ведь рассмотренная сегодня тема «Геометрия измерительных инструментов» ещё раз доказывает необходимость более тщательного изучения этого предмета. Я убедилась в том что не только геометрия возникла на основе практической деятельности людей, но и наша повседневная жизнь напрямую зависит от качества приобретённых в школе знаний. Использованная литература Петров В.А. «Прикладные задачи на уроках математики» – М., 2006г. Гольшин В.Н. « Простейшие измерения на местности» – М., 1964г. Иванов А.И. «Технические измерения» – М., 1964г. Иванов П.А. «Основы геодезии, топографии и картографии» – М., 1972г. «Измерительные приборы в машиностроении» – М., 1964г. Лиман М.М. «Конструирование учащимися наглядных пособий по геометрии» – М., 1965г. Сосянц В.Г. «Городские рельсовые пути и дороги» – М., 1965г. Оглоблин А.М. «Основы токарного дела» – М.,1975г. «Летняя практика по геоботанике» – Л., 1983г. |
