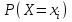Геометрия Теоретические вопросы
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
|
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО УЧЕБНОЙ ДИСЦИПЛИНЕматематика Памурзина Маргарита Александровна Раздел 1.Геометрия Теоретические вопросы: Основные понятия и формулы планиметрии. Параллельность и перпендикулярность в пространстве. Координаты в пространстве: декартовы координаты, расстояние между точками, координаты середины отрезка. Векторы в пространстве: определение координат вектора, нахождение координат середины отрезка, определение длины вектора, условия параллельности и перпендикулярности, равенство векторов. Призма (прямая, наклонная, правильная): определение, составляющие, сечения, площадь поверхности, объем. Параллелепипед: определение, свойства, площадь поверхности, объем. Пирамида: определение, виды, свойства, сечения, площадь поверхности, объем. Цилиндр: определение, составляющие, свойства, сечения, площадь поверхности, объем. Конус: определение, составляющие, свойства, сечения, площадь поверхности, объем. Шар: определение, составляющие, свойства, сечения, площадь поверхности, объем. Типовые тестовые задания: 1. Усечённый конус может быть получен вращением… 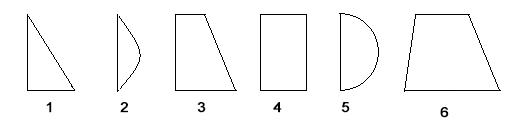 а) 1; б) 2; в) 3; г) 4; д) 5. 2. Цилиндр может быть получен вращением…  а) 1; б) 2; в) 3; г) 4; д) 5. 3. Сечение пирамиды плоскостью, перпендикулярной основанию и проходящей через вершину, есть … а) прямоугольник; б) треугольник; в) трапеция; г) квадрат. 4. Сечение цилиндра плоскостью, параллельной его образующим, есть … а) прямоугольник; б) треугольник; в) трапеция; г) квадрат. 5. Сечение конуса плоскостью, параллельной основанию, есть … а) прямоугольник; б) треугольник; в) трапеция; г) круг. 6. Координаты вектора 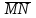 , если , если 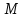 (13; 0; 2) и (13; 0; 2) и 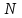 (0; 2; 13): (0; 2; 13): а) (13; 2; 15); б) (13; -2; -11); в) (-13; 2; 11); г) (11; -2; -13). 7. Абсолютная величина вектора 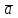 ( 0; 6; 8) равна… ( 0; 6; 8) равна…а) 14; б) 2; в) 10; г) 8. 8. Длина отрезка, соединяющего точки А(2; 0; -1) и К(3; -2; 1), равна … а) 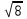 ; б) 3; в) 1; г) ; б) 3; в) 1; г) 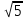 . . 9. Значение (значения) 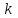 , при котором векторы , при котором векторы 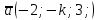 и и 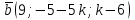 перпендикулярны перпендикулярныа) 2; б) -3,6; в) 2 и -3,6; г) -2 и 3,6. 10. Значение (значения) m, при котором векторы 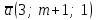 и и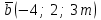 перпендикулярны перпендикулярныа) 2; б) 4; в) 4 и 2; г) -4 и -2. 11. Значения х и 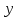 , при которых векторы , при которых векторы 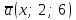 и и 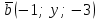 коллинеарны коллинеарныа) 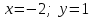 ; б) ; б) 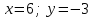 ; в) ; в) 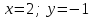 ; г) ; г) 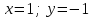 . . 12. Значения 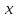 и и 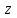 , при которых векторы , при которых векторы 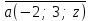 и и 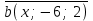 коллинеарны коллинеарныа) 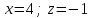 ; б) ; б) 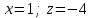 ; в) ; в) 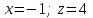 ; г) ; г) 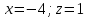 . . 13. Высота конуса 6 дм, образующая 10 дм. Площадь боковой поверхности конуса равна … а) 36  дм дм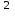 ; б) 60 дм ; б) 60 дм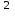 ; в)80 ; в)80 дм дм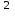 ; г) 100 дм ; г) 100 дм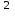 14.Объем цилиндра с радиусом 4м и высотой 3м равен… а) 48  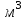 ; б) ; б) 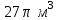 ; в) ; в) 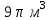 ; г) ; г) 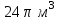 . .15.Площадь боковой поверхности правильной четырехугольной пирамиды со стороной основания 8 см и высотой 3 см равна… а) 24 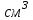 ; б) 80 ; б) 80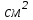 ; в) 48 ; в) 48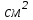 ; г) 144 ; г) 144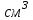 . .16. Площадь полной поверхности куба с ребром 6 см. а) 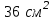 ; б) ; б)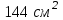 ; в) ; в)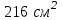 ; г) 100 ; г) 100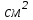 . .17. Апофема правильной четырехугольной пирамиды равна 6см., а боковая грань наклонена к плоскости основания под углом 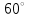 . Объем пирамиды равен . Объем пирамиды равена) 36 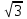 см см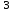 ; б) 40см ; б) 40см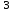 ; в) 18 ; в) 18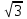 см см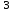 ; г) 25 ; г) 25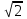 см см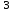 . . 18.Площадь сферы, если ее диаметр 6 м, равна… а) 184 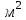 ; б) 184 ; б) 184 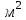 ; в) 36 ; в) 36 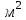 ; г) 63 ; г) 63 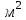 . . 19. Стороны основания прямой треугольной призмы 13 см, 14 см, 15 см. Длина бокового ребра – 10 см. Объём призмы равен … а) 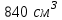 ; б) ; б) 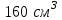 ; в) ; в) 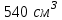 ; г) ; г) 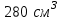 . .Раздел 2. Алгебра и начала анализа Теоретические вопросы: Функции и их свойства. Корень n-ой степени и его свойства. Степень с рациональным показателем и её свойства. Синус, косинус, тангенс и котангенс числового аргумента. Формулы тригонометрии. Тригонометрические функции, свойства и графики. Обратные тригонометрические функции. Понятие логарифма и его свойства. Показательная функция, её свойства и график. 9. Логарифмическая функция, её свойства и график. 10. Иррациональные уравнения. 11. Показательные уравнения и неравенства. 12. Логарифмические уравнения и неравенства. 13. Производная функции. 14. Геометрический и физический смысл производной. 15. Таблица производных. 16. Правила вычисления производных. 17. Необходимо условие возрастания и убывания функции. 18. Необходимое и достаточное условие экстремума функции. 19. Первообразная. Основное свойство первообразных. 20. Правила нахождения первообразных.Таблица первообразных. 21. Интеграл. 22. Вычисление площади плоских фигур с помощью определённого интеграла. 23. Комплексные числа. Действия над комплексными числами. Типовые тестовые задания: 1. Значениевыражения 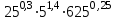 равно … равно …а) 25; б) 125; в) 5; г) 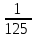 . . 2. Значение выражения 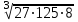 равно … равно …а) 15; б) 60; в) 30; г) 18. 3. Значение выражения 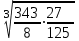 равно … равно …а) 21; б) 3,5; в) 13; г) 2,1. 4. Значение выражения 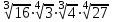 равно … равно …а) 6; б) 12; в) 10; г) 18. 5. Значение выражения 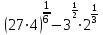 равно … равно …а) 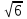 ; б) 12; в) 0; г) 6. ; б) 12; в) 0; г) 6. 6. Решение уравнения 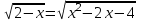 а) -2; б) -2 и 3; в) -3; г) 3. 7. Решение уравнения 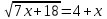 а) 1 и -2; б) 2; в) -2; г) 1. 8. Значение выражения 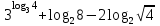 равно … равно …а) 9; б) 5; в) 4; г) 3. 9. Значение выражения 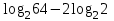 равно … равно …а) 2; б) 4; в) 3; г) 6. 10. Значение выражения 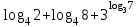 равно … равно …а) 10; б) 9; в) 4; г) 0. 11. Значение выражения 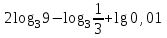 а) -1; б) 4; в) -4; г) 3. 12. Значение выражения 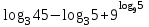 равно… равно…а) 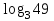 ; б) 7; в) ; б) 7; в) 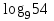 ; г) 0. ; г) 0. 13. График функции, заданной формулой 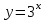 . .а) б) в) г) 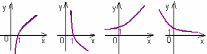 14. График функции, заданной формулой 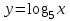 . .а) б) в) г) 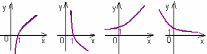 15. График функции, заданной формулой 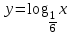 . .а) б) в) г) 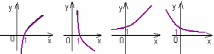 16. График функции, заданной формулой 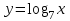 . .а) б) в) г)  17. Функция,график которой изображён на рисунке 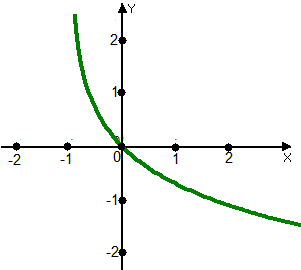 а) 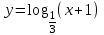 ; б) ; б) 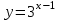 ; в) ; в) 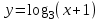 ; г) ; г)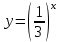 . .18. Функция,график которой изображён на рисунке 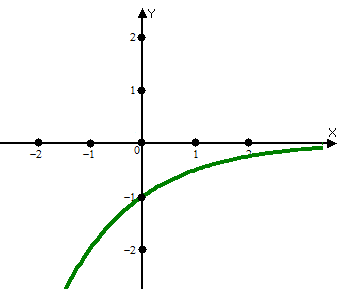 а) 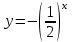 ; б) ; б) 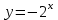 ; в) ; в) 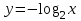 ; г) ; г)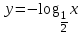 . . 19. Функция,график которой изображён на рисунке 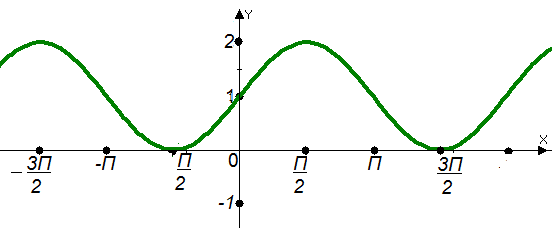 а) 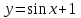 ; б) ; б) 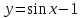 ; в) ; в) 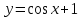 ; г) ; г) 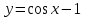 . .20. Выберите функцию,график которой изображён на рисунке 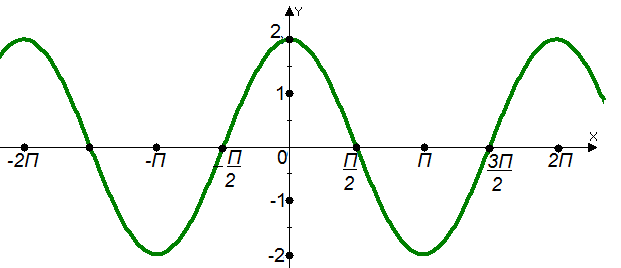 а) 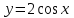 ; б) ; б) 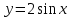 ; в) ; в) 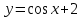 ; г) ; г) 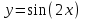 . .21. Корень уравнения 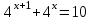 . .а) 2; б) -1; в) 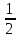 ; г) 0. ; г) 0.22. Корень уравнения 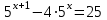 . .а) -1; б) 1; в) 2; г) 0. 23. Решение уравнения 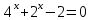 . .а) -1; б) 1; в) 2; г) 0. 24. Решениеуравнения 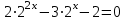 . .а) -1; б) 1;в) 2; г) 0. 25. Решение неравенства 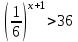 . .а) (- 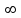 ;-3); б) (- ;-3); б) (-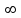 ;-3];в) [-3;+ ;-3];в) [-3;+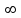 );г) );г) 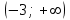 . .26. Решение неравенства 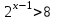 . .а) (- 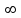 ;-2); б) (-2;+ ;-2); б) (-2;+ ); в) (4;+ ); в) (4;+ ); г) (- ); г) (- ;4). ;4).27. Решение неравенства 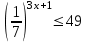 . .а) (- 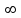 ;-1]; б) (- ;-1]; б) (-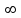 ;-3]; в) [-3;+ ;-3]; в) [-3;+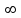 ); г) [-1;+ ); г) [-1;+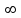 ). ).28. Решение неравенства 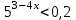 . .1) (- 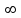 ;1]; 2) (- ;1]; 2) (-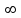 ;-1];3) (1;+ ;-1];3) (1;+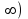 ; 4) [1;+ ; 4) [1;+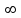 ). ).29. Корень уравнения 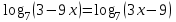 равен … равен …а) уравнение не имеет корней; б) -4; в) -5; г) 1. 30. Корень уравнения 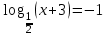 равен … равен …а) -1; б) -4; в) -5; г) 1. 31. Корень уравнения 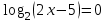 равен … равен …а) -1; б) 4; в) -3; г) 3. 32. Корень уравнения 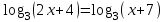 равен … равен …а) -1; б) 4; в) -3; г) 3. 33. Решением неравенства log 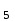 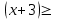 log5 log5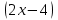 является промежуток … является промежуток …а) 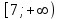 ; б) ; б) 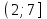 ; в) ; в) 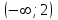 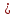 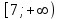 ; г) ; г) 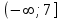 . . 34. Решением неравенства log 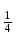 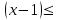 1 является промежуток … 1 является промежуток …а) 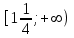 ; б) ; б) 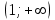 ; в) ; в) 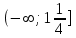 ; г) ; г) 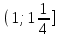 . . 35. Решением неравенства  log log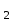 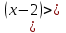 1 является промежуток … 1 является промежуток …а) 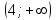 ; б) ; б) 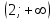 ; в) ; в) 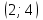 ; г) ; г) 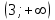 . . 36. Решением неравенства log 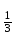 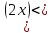 log log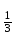 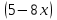 является промежуток … является промежуток …а) 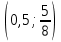 ; б) ; б) 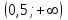 ; в) ; в) 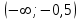 ; г) ; г) 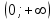 . . 37. Область определения функции 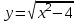 а) 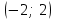 ; б) ; б) 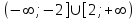 ; в) ; в) 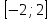 ; г) ; г) 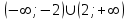 . . 38. Область определения функции 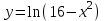 а) 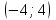 ; б) ; б) 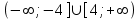 ; в) ; в) 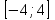 ; г) ; г) 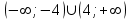 . . 39. Область определения функции 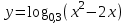 а) 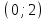 ; б) ; б) 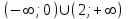 ; в) ; в) 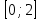 ; г) ; г) 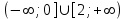 . . 40. Область определения функции у = 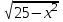 а) 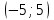 ; б) ; б) 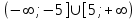 ; в) ; в) 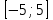 ; г) ; г) 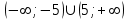 . . 41. Значение 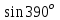 . .а) - 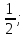 б) б) 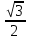 ;в) - ;в) -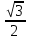 ;г) ;г)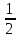 . .42. Значение 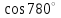 . .а)- 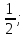 б) б) 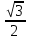 ;в) - ;в) -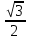 ; г) ; г)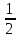 . .43. Значение 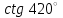 . .а) 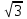 ; б) ; б)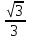 ;в) - ;в) -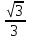 ;г) - ;г) -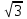 . .44. Значение 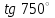 . .а) - 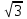 ; б) ; б)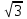 ; в) - ; в) -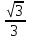 ; г) ; г)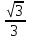 . .45. Значение выражения 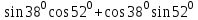 . .а) 0; б) 1; в) 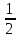 ; г) ; г) 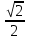 . .46. Значение выражения 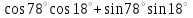 . .а) 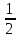 ; б) - ; б) -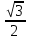 ;в)- ;в)-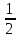 ;г) ;г) 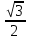 . .47. Значение выражения 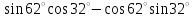 . .а) 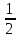 ;б) ;б) 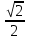 ;в) - 1; г) ;в) - 1; г)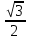 . .48. Значение выражения 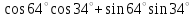 . .а) 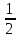 ; б) - ; б) -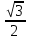 ;в)- ;в)-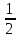 ;г) ;г) 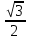 . .49. Вид функции 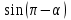 после приведения к функции угла после приведения к функции угла 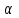 а) -cos 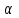 ; б) cos ; б) cos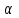 ; в) -sin ; в) -sin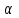 ; г) sin ; г) sin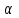 . .50. Вид функции 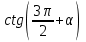 после приведения к функции угла после приведения к функции угла 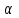 а) 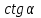 ; б) ; б) 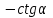 ; в) ; в) 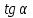 ; г) ; г) 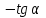 . .51. Вид функции 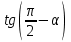 после приведения к функции угла после приведения к функции угла 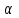 а) 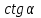 ; б) ; б) 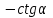 ; в) ; в) 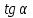 ; г) ; г) 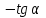 . .52. Вид функции 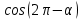 после приведения к функции угла после приведения к функции угла 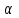 а) -cos 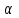 ; б) cos ; б) cos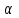 ; в) -sin ; в) -sin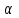 ; г) sin ; г) sin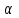 . .53. Производная функции 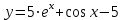 . .а) 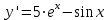 ; б) ; б) 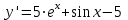 ; ;в) 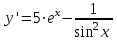 ; г) ; г) 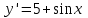 . .54. Производная функции 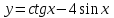 . .а) 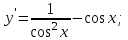 б) б) 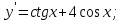 в) 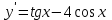 ; г) ; г) 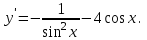 55. Производная функции 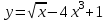 . .а) 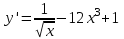 ; б) ; б) 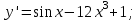 в) 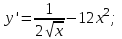 г) г) 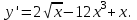 56. Производная функции 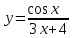 . .а) 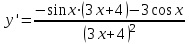 ;б) ;б) 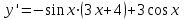 ; ;в) 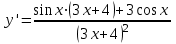 ; г) ; г) 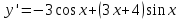 . .57. Производная функции 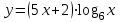 . .а) 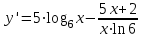 ; б) ; б) 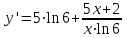 ; ;в) 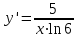 ;г) ;г) 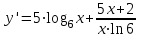 . .58. Производная функции 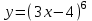 . .а) 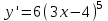 ; б) ; б)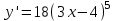 ; в) ; в) 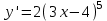 ; г) ; г) 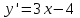 . .59. Производная функции 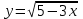 . .а) 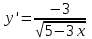 ; б) ; б) 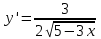 ; в) ; в) 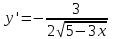 ; г) ; г) 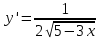 . .60. Производная функции 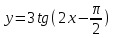 . .а) 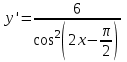 ;б) ;б) 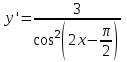 ; ;в) 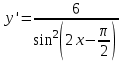 ;г) ;г) 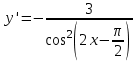 . .61. Производная функции 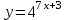 а) 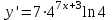 ;б) ;б) 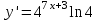 ; в) ; в) 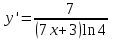 ;г) ;г) 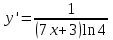 . .62. Тангенс угла наклона касательной 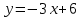 а) -3; б) 3; в) 6; г) -6. 63. Тангенс угла наклона касательной 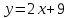 а) -2; б) 2; в) 9; г) 1. 64. Тангенс угла наклона касательной 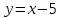 а) -5; б) 5; в) 1; г) -1. 65. Точка максимум функции 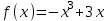 . .а) 1; б) -1; в) -2; г) 2. 66. Точка минимумафункции 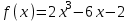 . .а) -1; б) 1; в) 6;г) -2. 67. Минимум функции 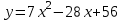 . .а) 56; б) 28; в) 7; г) 0. 68. Максимум функции 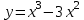 . .а) -3; б) 3;в) -4; г) 0. 69. Критические точки функции 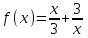 . .а)  б) б) ;в) ;в)  г) г)  70. Критические точки функции 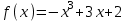 . .а) 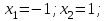 б)x =1;в)x = -1; г) б)x =1;в)x = -1; г) 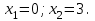 71. Общий вид первообразной функции 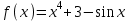 а) 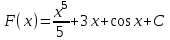 ;б) ;б) 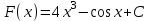 ; ;в) 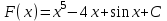 ;г) ;г) 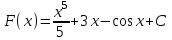 . .72. Общий вид первообразной функции 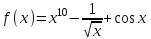 . .а) 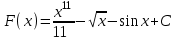 ;б) ;б) 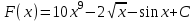 ; ;в) 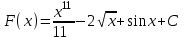 ;г) ;г) 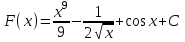 . .73. Общий вид первообразной функции 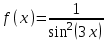 а) 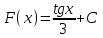 ;б) ;б) 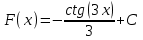 ; ;в) 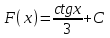 ;г) ;г) 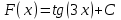 . .74. Общий вид первообразной функции 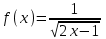 на промежутке на промежутке 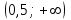 . .а) 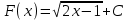 ;б) ;б) 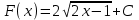 ; ;в) 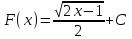 ;г) ;г) 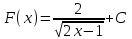 . .75. Интеграл 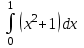 . .а) 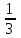 ; б) ; б) 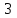 ; в) ; в) 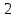 ; г) ; г) 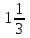 . .76. Интеграл 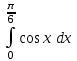 . .а) 1; б) 0,5;в) 1,5; г) 2. 77. Интеграл 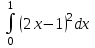 . .а) 1; б) 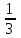 ; в) 4; г) ; в) 4; г)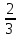 . .78. Площадь фигуры, ограниченной линиями 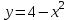 , , 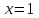 , , 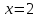 , , 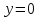 а) 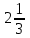 ; б) ; б) 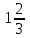 ;в) ;в) 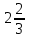 ; г) ; г) 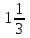 . .79. Площадь фигуры, ограниченной линиями 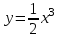 , , 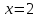 , , 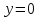 . .а) 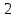 ; б) ; б) 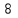 ; в) ; в) 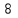 ; г) ; г) 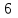 . .80. Значение комплексного числа 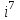 . .а) -1; б) 1; в) i; г) –i. 81. Значение комплексного числа 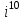 . .а) -1; б) 1; в) i; г) –i. 82. Сумма комплексных чисел 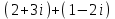 . .а) 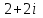 ; б) ; б) 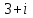 ; в) ; в) 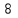 ; г) ; г) 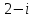 . .83. Разность комплексных чисел 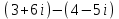 . .а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . .84. Произведение комплексных чисел 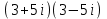 . .а) 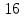 ; б) ; б) 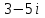 ; в) ; в) 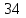 ; г) ; г) 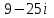 . .85. Деление комплексных чисел 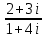 . .а) 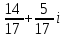 ; б) ; б) 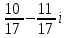 ; в) ; в) 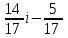 ; г) ; г) 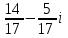 . .Раздел 3.Комбинаторика, теория вероятностей и статистика Теоретические вопросы: Выборка. Факториал. Размещения, перестановки и сочетания без повторений и с повторениями. Виды событий: случайные, невозможные, достоверные, совместные, несовместные, независимые, противоположные. Вероятность. Свойства вероятностей. Числовые характеристики выборок. Элементы математической статистики. Типовые тестовые задания: 1. Значение 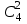 . .а) 6; б) 8; в) 12; г) 10. 2. Значение 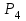 . .а) 24; б) 6; в) 12; г) 4. 3. Значение 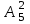 . .а) 12; б) 20; в) 10; г) 24. 4. Значение 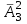 . .а) 9; б) 3; в) 8; г) 6. 5. Совет колледжа состоит из семи студентов. Количество различных вариантов выбора председателя совета, его заместителя и секретаря равно … а) 720; б) 240; в) 210; г) 5040. 6. Количество различных вариантов выбора 3 лиц в совет колледжа из группы, в которой учится 12 человек, равно … а) 720; б) 220; в) 210; г) 5040. 7. Каждая буква слова МАТЕМАТИКА написана на разных карточках. Количество различных способов переставить эти буквы равно … а) 10540; б) 40320; в) 5040; г) 151200. 8. Вероятность того, что второй парой по расписанию будет математика, равна 0,97. Вероятность того, что математику отменят,равна ... а) 1; б) 0,9; в) 0,03; г) 0,3. 9. Вероятность выпадения 4 очков при одном бросании игрального кубика равна … а) 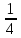 ; б) ; б) 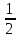 ; в) ; в) 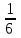 ; г) 1. ; г) 1.10. Вероятность выпадения 7 очков при одном бросании игрального кубика равна … а) 1; б) 0,9; в) 0,5; г) 0. 11. Случайная величина Х задана рядом распределения
Математическое ожидание равно … а) 0,5; б) 0,6; в) 0,9; г) 1,3. 12. Случайная величина Х задана рядом распределения
Математическое ожидание равно … а) 0,5; б) 0,6; в) 1; г) 0,3. 13. Результаты опроса 20 студентов 2 курса приведены в таблице:
Частота появления ответа «ДА» равна … а) 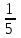 ; б) ; б) 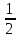 ; в) ; в) 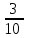 ; г) ; г) 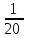 . .14. Результаты контрольных работ 30 учащихся приведены в таблице:
Частота появления оценки «5» равна ... а) 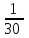 ; б) ; б) 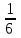 ; в) ; в) 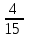 ; г) ; г) 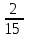 . . |