проект Геометрия вокруг нас. Геометрия вокруг нас
 Скачать 4.28 Mb.
|
|
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ Тема: «Геометрия вокруг нас» Выполнил(а): Иванова Полина, Студентка 1 курса Специальность Дошкольное образование Руководитель проекта: Роганова Ирина Викторовна, преподаватель математики СОДЕРЖАНИЕ ВВЕДЕНИЕ………………………………………………………........3 ГЛАВА 1.ГЕОМЕТРИЯ ВОКРУГ НАС 1.1 Геометрия у древних людей…………………………………….....5 1.2 Геометрия в быту…………………………………………….….....7 1.3 Геометрия в архитектуре…………………………………….……8 1.4 Геометрия в транспорте…………………………………………..11 1.5 Комбинации геометрических тел в окружающем мире………..12 1.6 Природные творения в виде геометрических фигур…………..13 1.7 Геометрические формы и животные…………...........................14 1.8 Фрактальный мир вокруг нас…………………………………....15 1.9 Геометрия вселенной……………………………………………16 ЗАКЛЮЧЕНИЕ……………………………………………………...18 СПИСОК ЛИТЕРАТУРЫ…………………………………………...19 ВВЕДЕНИЕ В начале XX века великий французский архитектор Ле Корбюзье сказал: «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». Геометрия возникла очень давно, это одна из самых древних наук. Заглянем в прошлое, когда зародилась наука геометрия.... Более двух тысяч лет назад в Древней Греции впервые стали складываться и получили первоначальное развитие основные представления и обоснования науки геометрии. Этому периоду развития геометрии предшествовала многовековая деятельность сотен поколений наших предков. Первоначальные геометрические представления появились в результате практической деятельности человека и развивались чрезвычайно медленно. Еще в глубокой древности, когда люди питались только тем, что им удавалось найти и собрать, им приходилось переходить с места на место. В связи с этим они приобретали некоторые представления о расстоянии. Вначале, надо полагать, люди сравнивали расстояние по времени, в течении которого они проходили. Например, если от реки до леса можно было дойти за время от восхода солнца до его захода, то говорили: река от леса находится на расстоянии дня ходьбы. Каждый из нас без труда сможет привести примеры различных геометрических тел, встречающихся в окружающем нас мире: жилой дом, камень, дерево, капля воды и многое другое. А с многими геометрическими понятиями мы уже знакомы: круг, квадрат, угол, куб, измерение отрезков, площадь, объем и так далее. И если взглянуть на окружающие нас предметы как на геометрические тела, то можно сказать, например, что дом и кирпич имеют одинаковую форму – форму параллелепипеда и отличаются лишь размерами. При изучении геометрических тел не берется во внимание, из какого материала они сделаны, какого цвета, в каком состоянии находятся. Этим занимается физика, химия, биология. Изучая геометрию нас будет интересовать только форма и размеры предметов, их взаимное расположение. Любой современный человек в своей жизни не может обойтись без знания математики, а в частности без умений увидеть в окружающем нас мире геометрические тела и объекты. Цель работы – изучить в каких областях встречаются геометрические фигуры, геометрические тела Задачи: - рассмотреть использование геометрических форм и линий в практической деятельности человека; - изучить некоторые природные творения в виде геометрических фигур; - изучить возникновение науки «геометрия» Методы исследования: анализ печатных источиков, анализ интернет-ресурсов ГЛАВА 1.ГЕОМЕТРИЯ ВОКРУГ НАС 1.1. Геометрия у древних людей.   Треугольники, квадраты, ромбы, окружности… каждый ученик сталкивается с ними в школе на уроках геометрии.Научная формулировка гласит, что геометрия – это раздел математики, который изучает пространственные фигуры и формы. Ещё в эпоху неолита люди составляли на стенах пещер орнаменты из треугольников, ромбов, прямоугольников, кругов. Древние художники тонко чувствовали красоту геометрических форм; наскальные рисунки, выполненные с большой любовью к природе, радовали глаз. Человек отмечал равенство, симметрию, подобие фигур. Со временем он научился  использовать свойства фигур в практической жизни. Геометрия – древнейшая наука, а первые геометры производили расчеты свыше тысячи лет назад.Земледельцы, жившие на берегах великих рек: Нила, Тигра и Ефрата, Инда и Ганга, искусно делили свои земельные участки. Для проведения замеров были выработаны первые правила новой науки – «геометрии», что в переводе с греческого и означает – «землемерие».  Геометрические фигуры интересовали наших предков не только потому, что помогали решать практические задачи. Некоторые из фигур имели для людей магическое значение. Так, треугольник считался символом жизни, смерти и возрождения; квадрат – символом стабильности. Вселенную, бесконечность обозначали правильным пятиугольником – пентагоном, правильный шестиугольник – гексагон, являлся символом красоты и гармонии. Круг – знаком совершенства. 1  .2. Геометрия в быту.С   тены, пол и потолок являются прямоугольниками (не будем обращать внимания на проёмы окон и дверей). Комнаты, кирпичи, шкаф, железобетонные блоки, напоминают своей формой прямоугольный параллелепипед. Посмотрим на паркетный пол. Планки паркета – прямоугольники или квадраты. Плитки пола в ванной, метро, на вокзалах чаще бывают правильными шестиугольниками или восьмиугольниками, между которыми уложены небольшие квадратики.Многие вещи напоминают окружность – обруч, кольцо, дорожка вдоль арены цирка. Арена цирка, дно стакана или тарелки имеют форму круга. Фигура, близкая к кругу, получится, если разрезать поперек арбуз. Нальем в стакан воду. Её поверхность имеет форму круга. Если наклонить стакан, чтобы вода не выливалась, тогда край водной поверхности станет эллипсом. А у кого-то есть столы в виде круга, овала или очень плоского параллелепипеда. С 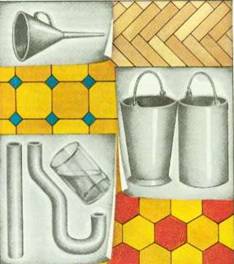  о времени изобретения гончарного круга люди научились делать круглую посуду – горшки, вазы. На геометрический шар похожи арбуз, глобус, разные мячи (футбольный, волейбольный, баскетбольный).П оэтому, когда у футбольных болельщиков до матча спрашивают, с каким счетом он кончится, они часто отвечают: «Не знаем – мяч круглый» Ведро имеет форму усеченного конуса, у которого верхнее основание больше нижнего. Впрочем, ведро бывает и цилиндрической формы. Вообще, цилиндров и конусов в окружающем нас мире очень много: трубы парового отопления, кастрюли, бочки, стаканы, абажур, кружки, консервная банка, круглый карандаш, бревно и др 1.3. Геометрия в архитектуре.   Дом приблизительно имеет вид прямоугольного параллелепипеда. В современной архитектуре смело используются самые разные геометрические формы. Многие жилые дома, общественные здания украшаются колоннами.О    кружность как геометрическая фигура всегда привлекала к себе внимание художников, архитекторов. В неповторимом архитектурном облике Санкт - Петербурга восторг и удивление вызывает «чугунное кружево» - садовые ограды, перила мостов и набережных, балконные решетки и фонари. Четко просматриваемое на фоне фасада зданий летом, в изморози зимой, оно придает особое очарование городу.  Особую воздушность придают воротам Таврического дворца (созданного в конце ХIII в. архитектором Ф.И.Волковым) окружности сплетенные в орнамент. Торжественность и устремленность ввысь – такой эффект в архитектуре зданий достигается использованием арок, представляющих дуги окружностей. Это видим на здании Главного штаба (Санкт-Петербург). А  рхитектура православных церквей включает в себя как обязательные элементы купола, арки, округлые своды, что зрительно увеличивает пространство, создает эффект полета, легкости. А  как красив Московский Кремль. Прекрасны его башни! Сколько интересных геометрических фигур положено в их основу! Например, Набатная башня. На высоком параллелепипеде стоит параллелепипед поменьше, с проемами для окон, а ещё выше воздвигнута четырехугольная усечённая пирамида. На ней расположены четыре арки, увенчанные восьмиугольной пирамидой. Геометрические фигуры различной формы можно узнать и в других замечательных сооружениях, возведенных русскими зодчими.  Выразительный контраст треугольника и прямоугольника на фасаде привлекает внимание посетителей музея Гронингена (Голландия). К   руглая, прямоугольная, квадратная – все эти формы прекрасно уживаются в здании Музея современного искусства в Сан-Франциско (США). Здание Центра современного искусства имени Жоржа Помпиду в Париже – сочетание гигантского прозрачного параллелепипеда с ажурной металлической арматурой. Главные элементы здания больницы в Берлине (Германия) – прямоугольники и окружности. Геометрическая форма железнодорожной станции в аэропорту Лиона (Франция) напоминает древнюю гигантскую птицу и при этом сооружение суперсовременно.А  сколько геометрических фигур можно найти в конструкциях мостов. На парапете моста часто укрепляют спасательные круги. Они по форме очень близки к тору.К   онечно, каждого европейца оказавшегося на далеком австралийском континенте привлекают, прежде всего, две главные достопримечательности Сиднея, ставшие его символами и настоящей национальной гордостью. Это самое известное здание Сиднея – оперный театр, построенный на мысе Беннелонг-Пойнт по проекту датского архитектора Йорна Утзона. Э  то впечатляющее сооружение, похожее на несущийся по водам залива парусник, строилось 14 лет и было торжественно открыто 20 октября 1973 года. Сиднейская опера состоит из трех залов, где проходят театральные представления и концерты классической и современной музыки, а также работает большая студия звукозаписи. Кстати, значительные средства на строительство знаменитого здания когда-то дала специально организованная лотерея. Архитектурные ансамбли музеев мира поражают своим величием, красотой, грацией. Их неповторимый облик невольно притягивает наши взгляды, волнует наше воображение. Каждый из них прекрасен по-своему и заставляет наши мысли парить в свободном полете мечты и фантазии. Музей Royal Ontario, Торонто. Этот музей больше похож на космический корабль, потерпевший крушение, нежели на обычное здание. Национальный музей искусств, Осака. Архитекторы создали этот музей в виде гигантского металлического насекомого, которое пока еще на земле, но уже готовится к полету. G  uggenheim Museum Bilbao. Этот музей вызывает ассоциацию со свернувшейся змеей, которая мирно дремлет на солнышке. 1  .4. Геометрия транспорта. По улице движутся автомобили, трамваи, троллейбусы. Их колеса с геометрической точки зрения – круги. В окружающем нас мире встречается много различных поверхностей, сложных по форме, не имеющих специальных названий.  Паровой котел напоминает цилиндр. В нем находится пар под высоким давлением. Поэтому стенки цилиндра слегка (незаметно для глаза) изгибаются, образуя поверхность очень сложной и неправильной формы, которую инженеры должны знать, чтобы суметь правильно рассчитать котел на прочность. Сложную форму имеет и корпус подводной лодки. Он должен быть хорошо обтекаемым, прочным и вместительным. От формы корабельного корпуса зависит и прочность корабля, и его устойчивость и скорость. Результат работы инженеров над формой современных автомобилей, поездов, самолетов - высокие скорости движения. Если форма будет удачной, обтекаемой, сопротивление воздуха значительно уменьшается, за счет чего увеличивается скорость.Сложную форму имеют и детали машин – гайки, винты, зубчатые колеса и т.д.   Рассмотрим ракеты и космические корабли. Корпус ракеты состоит из цилиндра (в котором находятся двигатель и горючее), а в конической головной части помещается кабина с приборами или с космонавтом. 1.5. Комбинации геометрических тел в окружающем нас мире.  Телевизионная башня, построенная замечательным русским советским инженером В.Г. Шуховым. Она состоит из частей, которые математики называют гиперболоидами вращения. Хотя сами части кривые, они сложены из прямолинейных металлических балок. Этим Шухов облегчил возведение башни.   Колонны в большинстве случаев – цилиндры, но могут иметь и более сложную форму. А обелиски в память погибших – четырехгранные столбы, сужающиеся к верху. В 1908 году группу молодых французских художников в шутку прозвали кубистами за то, что они изображали мир в виде комбинаций геометрических фигур – куба, шара, цилиндра, конуса. Из насмешливого прозвища родилось новее художественное направление «кубизм», влияние которого распространилось на весь мир. Одна из таких работ картина Пабло Пикассо «Скрипка». А в таком «геометрическом» кресле вполне удобно сидеть.     1.6 Природные творения в виде геометрических фигур. Д  о сих пор рассматривали некоторые геометрические формы, созданные руками человека. Но ведь в самой природе очень много замечательных геометрических форм. Необыкновенно красивы и разнообразны многоугольники, созданные природой.К  ристалл соли имеет форму куба. Кристаллы горного хрусталя напоминают отточенный с двух сторон карандаш. Алмазы чаще всего встречаются в виде октаэдра, иногда куба. Существуют и многие микроскопические многоугольники. В микроскоп можно увидеть, что молекулы воды при замерзании располагаются в вершинах и центрах тетраэдров. Атом углерода всегда соединен с четырьмя другими атомами тоже в форме тетраэдра. Одна из самых изысканных геометрических фигур падает на нас с неба в виде снежинок.Обычная горошина имеет форму шара. И это неспроста. Когда стручок гороха созреет и лопнет, горошины упадут на землю и благодаря своей форме покатятся во все стороны, захватывая всё новые территории. Горошины кубической или пирамидальной формы так и остались бы лежать возле стебля. Шаровую форму принимают капельки росы, капли ртути из разбитого градусника, капли масла, оказавшиеся в толще воды… Все жидкости в состоянии невесомости обретают форму шара. Отчего шар так популярен? Это объясняется одним замечательным свойством: на изготовление шара расходуется значительно меньше материала, чем на сосуд любой другой формы того объёма. Поэтому, если вам нужен вместительный мешок, а ткани не хватает, шейте его в форме шара. Шар – единственное геометрическое тело, у которого наибольший объём заключен в наименьшую оболочку. 1.7 Геометрические формы и животные.  Принцип экономии хорошо «усвоили» животные. Сохраняя тепло, на холоде они спят, свернувшись в клубочек, поверхность тела уменьшается, и тепло лучше сохраняется. По этим же причинам северные народы строили круглые дома.Животные, конечно же, геометрию не изучали, но природа наделила их талантом строить себе дома в форме геометрических тел. Многие птицы – воробьи, крапивники, лирохвосты – строят свои гнёзда в форме полушара.Есть архитекторы и среди рыб: в пресных водах живет удивительная рыба колюшка. В отличие от многих своих соплеменников она живет в гнезде, которое имеет форму шара. Н  о самые искусные геометры – пчёлы. Они строят соты из шестиугольников. Любая ячейка в сотах окружена шестью другими ячейками. А основание, или донышко, ячейки представляет собой трехгранную пирамиду. Такая форма выбрана неспроста. В правильный шестиугольник поместится больше меда, а зазоры между ячейками будут наименьшими! Разумная экономия усилий и строительных материалов.  1.8 Фрактальный мир вокруг нас. Фракталы – уникальные объекты, порожденные непредсказуемыми движениями хаотического мира. Их находят в местах таких малых, как клеточная мембрана и таких огромных, как Солнечная система. Разветвления трубочек трахей, листья на деревьях, вены в руке, река, бурлящая и изгибающаяся, рынок ценных бумаг – это все фракталы. От представителей древних цивилизаций до Майкла Джексона, ученые, математики и артисты, как и все остальные обитатели этой планеты, были зачарованы фракталами и применяли из в своей работе. Программисты и специалисты в области компьютерной техники так же без ума от фракталов, так как фракталы бесконечной сложности и красоты могут быть сгенерированы простыми формулами на простых домашних компьютерах. Открытие фракталов было открытием новой эстетики искусства, науки и математики, а также революцией в человеческом восприятии мира.    Испытатель. Будущее. Аферист. Повторение РасширениеОтветственность   Актер. Граница. Последствия Вызов 1.9 Геометрия Вселенной Т 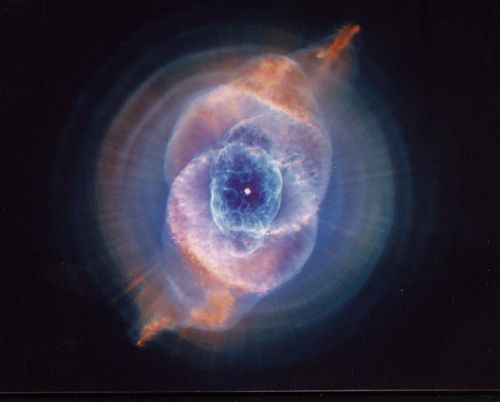 ысячелетиями пытливое человечество обращало свои взгляды на окружающий мир, стремилось постигнуть его, вырваться за пределы микромира в макромир. Величественная картина небесного купола, усеянного мириадами звезд, с незапамятных звезд волновала ум и воображение ученых, поэтов, каждого живущего на Земле и зачарованного любующегося торжественной и чудной картиной, по в ыражению Лермонтова.Вселенная бесконечна во времени и пространстве. Каждая частичка вселенной имеет свое начало и конец, как во времени, так и в пространстве, но вся Вселенная бесконечна и вечна так, как она является вечно самодвижущейся материей. Вселенная – это всё существующее. От мельчайших пылинок и атомов д  о огромных скоплений вещества звездных миров и звездных систем. Поэтому не будет ошибкой сказать, что любая наука так или иначе изучает Вселенную, точнее, тем или иначе её стороны. Химия изучает мир молекул, физика – мир атомов и элементарных частиц, биология – явления живой природы. Но существует научная дисциплина, объектом исследования которой служит сама вселенная или «Вселенная как целое». Это особая отрасль астрономии, так называемая космология. Космология – учение о Вселенной в целом, включающая в себя теорию всей охваченной астрономическими н  аблюдениями области, как части Вселенной, кстати, не следует смешивать понятия Вселенной в целом и «наблюдаемой» (видимой) Вселенной.Звезды во Вселенной объединены в гигантские Звездные системы, называемые галактиками. Звездная система. В составе которой, как рядовая звезда находится наше Солнце, называется Галактикой. Внешний вид галактик чрезвычайно разнообразен, и некоторые из них очень живописны. Эдвин Пауэлла Хаббл (1889-1953), выдающийся американский астроном – наблюдатель, избрал самый простой метод классификации галактик по внешнему виду. ЗАКЛЮЧЕНИЕ В своей работе мы исследовали, какие геометрические фигуры и тела окружают нас, и убедились, сколько самых разнообразных геометрических линий и поверхностей использует человек в своей деятельности – при строительстве различных зданий, мостов, машин, в транспорте. Пользуются им не из простой любви к интересным геометрическим фигурам, а потому, что свойства этих геометрических линий и поверхностей позволяют с наибольшей простотой решать разнообразные технические задачи. А природные творения не просто красивы, их форма целесообразна, то есть наиболее удобна. А человеку остается только учиться у природы – самого гениального изобретателя. Следует отметить, что работа над темой, помогла увидеть геометрию окружающего мира. Теперь мы смотрим и восхищаемся творениями человека или природы. Из всего сказанного можно сделать вывод, что геометрия в нашей жизни на каждом шагу играет очень большую роль. Она нужна не только для того, чтобы называть части строений или формы окружающего нас мира. С помощью геометрии мы можем решить многие задачи, ответить на многие вопросы.    Черная дыра искривляет вокруг себя геометрию Геометрия вазы Мыльная геометрия  Геометрия лета Геометрия лета  Здоровый эффект геометрии  Геометрия красоты Ландшафтная геометрия СПИСОК ЛИТЕРАТУРЫ 1.Детская энциклопедия.т.2-М.: «Педагогика», 2015 г. 2.Депман И.Я., Виленкин Н.Я. “За страницами учебника математики” Дрофа 2016 3. Каган В.Ф. Очерки по геометрии. - М.: Московский университет, 2017 г.. 4.Свечников А.А. Путешествие в историю математики или как люди научились считать. - М.: Просвещение, 2016 г. 5. http://www.informio.ru/publications/id4203/Geometrija (дата обращения 25.11.2019 года) 6. https://moluch.ru/young/archive/20/1330/ (дата обращения 12.01.2020 года) 7. http://tobemum.ru/deti/kak-nauchit/geometriya-dlya-de (дата обращения 09.02.2020 года) 8. https://www.moya-planeta.ru (дата обращения 29.03.2020 года.) |