ЛР_1.01_Исследование распределения случайной величины. Герт Антон Владимирович к работе допущен Работа выполнена отчет принят Рабочий протокол и отчет

• Название: Герт Антон Владимирович к работе допущен Работа выполнена отчет принят Рабочий протокол и отчет
• Анкор: Lab_1_01_otchet.docx
• Дата: 01.06.2022
• Размер: 2.47 Mb.
• Имя файла: ЛР_1.01_Исследование распределения случайной величины.docx
• Тип: Отчет; #561435

Санкт-Петербургский национальный исследовательский университет

информационных технологий, механики и оптики УЧЕБНЫЙ ЦЕНТР ОБЩЕЙ ФИЗИКИ ФТФ

Группа Т3131

Студент Даценко Ульяна

Преподаватель Герт Антон Владимирович

К работе допущен

Работа выполнена

Отчет принят

Рабочий протокол и отчет по лабораторной работе № 1.03. Исследование распределения случайной величины

1. 
   Цель работы.
   

• 
  Провести многократные измерения определенного интервала времени.
  
• 
  Построить гистограмму распределения результатов измерения.
  
• 
  Вычислить среднее значение и дисперсию полученной выборки.
  
• 
  Сравнить гистограмму с графиком функции Гаусса с такими же как и у экспериментального распределения средним значением и дисперсией.
  

2. 
   Задачи, решаемые при выполнении работы.
   

• 
  Выполнение многократных измерений, построение графиков в Excel, работа с формулами в программе по обработке табличных данных
  

3. 
   Объект исследования.
   

• 
  Многократные измерения
  

4. 
   Метод экспериментального исследования.
   

• 
  Замер 5-секундного интервала на секундомере
  
• 
  Обработка результатов многократных измерений с помощью специальных программ и формул
  

5. 
   Рабочие формулы и исходные данные.
   

• 
  среднеарифметическое всех результатов измерений: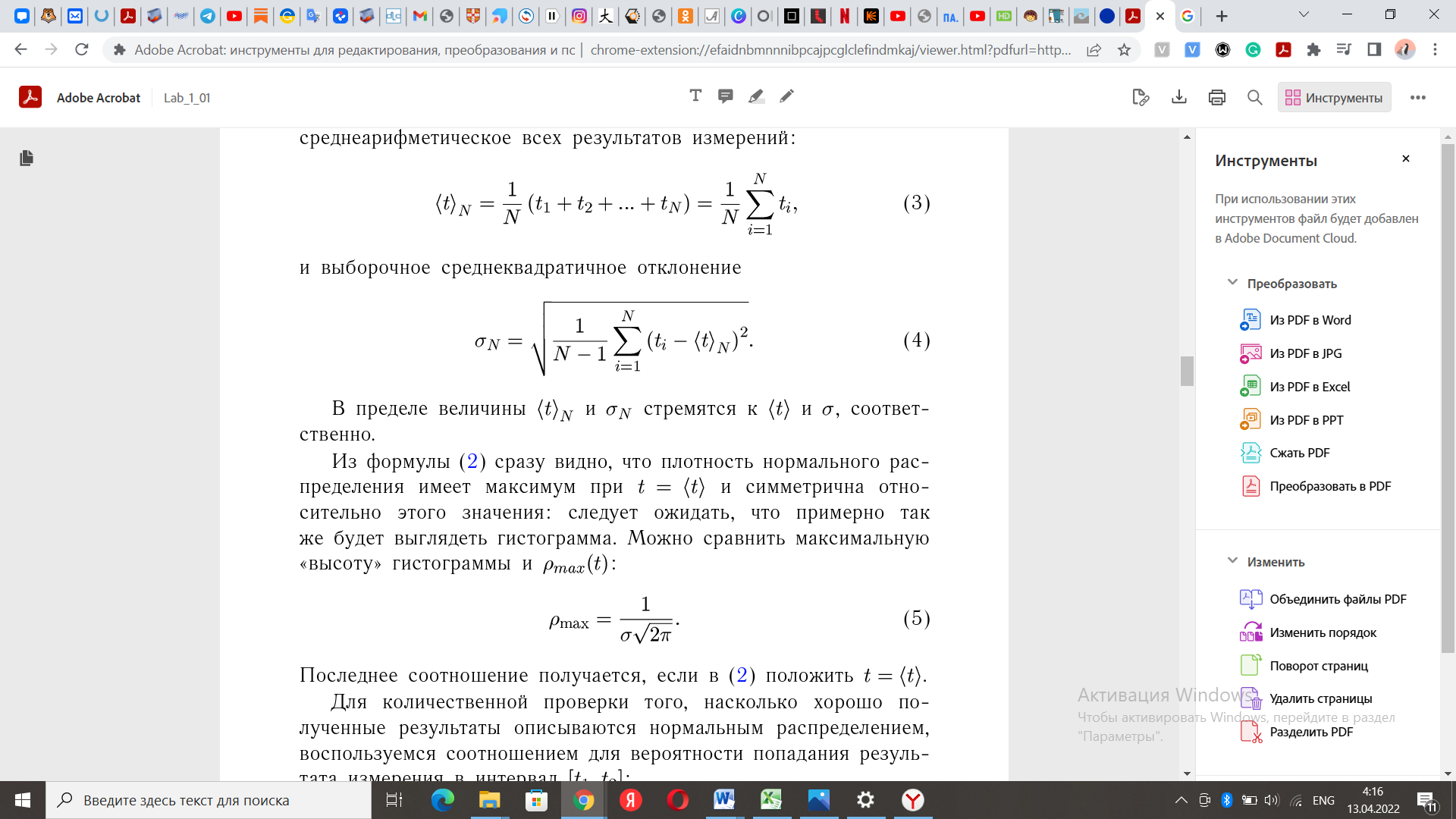
  

• 
  выборочное среднеквадратичное отклонение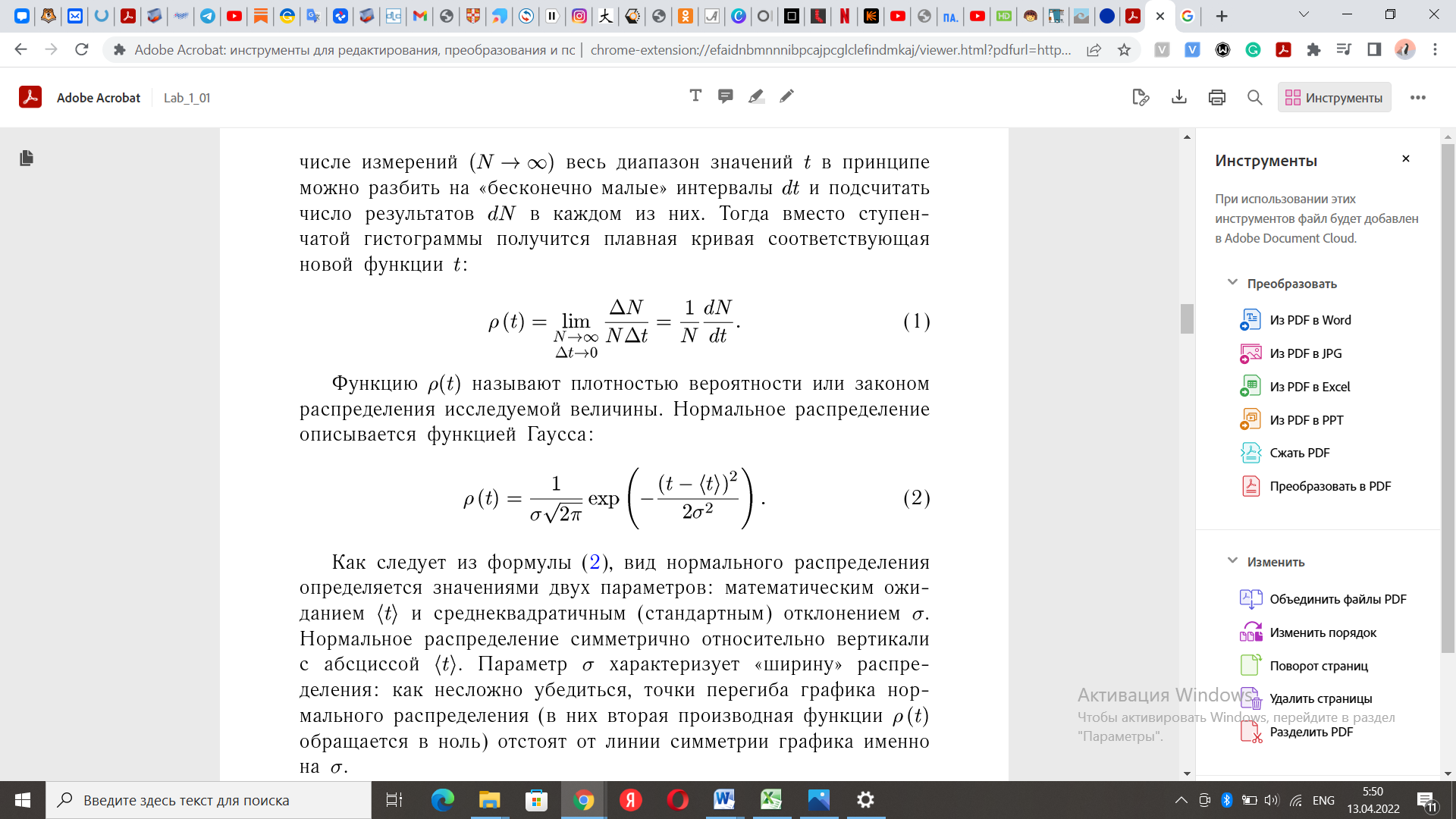
  

• 
  среднеквадратичное отклонение среднего значения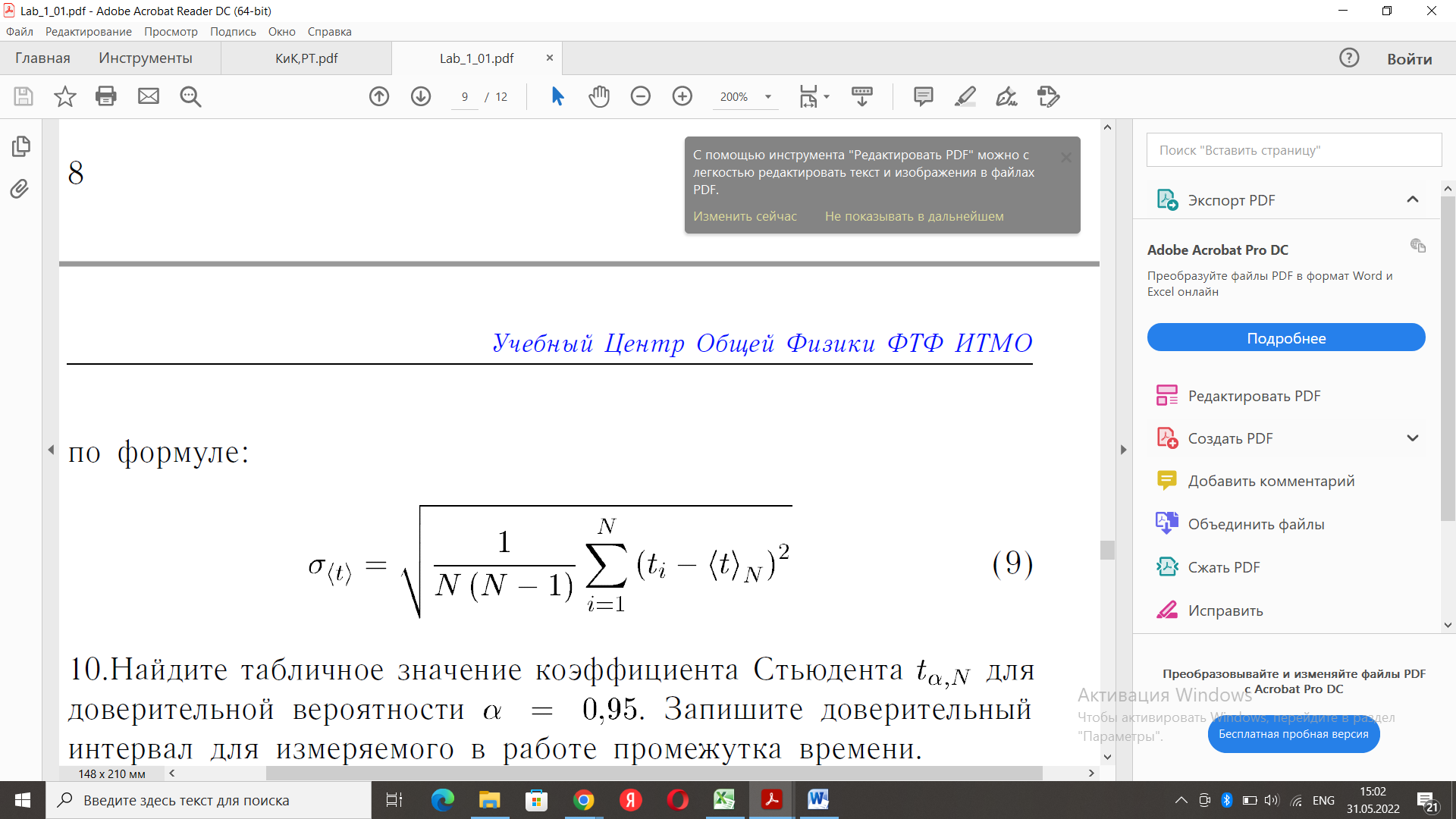
  

6. 
   Измерительные приборы.
   

   № п/п	Наименование	Тип прибора	Используемый диапазон	Погрешность прибора
   1	Секундомер	Измерение времени	0 мс – 99 часов	5 мс

7. 
   Результаты прямых измерений и их обработки (таблицы, примеры расчетов).
   

Таблица 1: Результаты прямых измерений

№	ti, с	ti − ⟨t⟩𝑁 , с	(ti − ⟨t⟩𝑁)2 , с2
1	4,73	-0,27	0,0729
2	4,67	-0,33	0,1089
3	5,06	0,06	0,0036
4	4,89	-0,11	0,0121
5	5,17	0,17	0,0289
6	4,58	-0,42	0,1764
7	5,34	0,34	0,1156
8	4,63	-0,37	0,1369
9	4,79	-0,21	0,0441
10	5,41	0,41	0,1681
11	4,82	-0,18	0,0324
12	5,21	0,21	0,0441
13	5,36	0,36	0,1296
14	5,81	0,81	0,6561
15	4,93	-0,07	0,0049
16	4,85	-0,15	0,0225
17	5,18	0,18	0,0324
18	4,94	-0,06	0,0036
19	4,63	-0,37	0,1369
20	5,24	0,24	0,0576
21	4,87	-0,13	0,0169
22	5,14	0,14	0,0196
23	4,69	-0,31	0,0961
24	5,28	0,28	0,0784
25	4,92	-0,08	0,0064
26	4,83	-0,17	0,0289
27	5,04	0,04	0,0016
28	4,94	-0,06	0,0036
29	5,11	0,11	0,0121
30	4,88	-0,12	0,0144
31	5,13	0,13	0,0169
32	5,10	0,10	0,0100
33	4,96	-0,04	0,0016
34	4,81	-0,19	0,0361
35	5,08	0,08	0,0064
36	4,84	-0,16	0,0256
37	4,93	-0,07	0,0049
38	5,04	0,04	0,0016
39	5,12	0,12	0,0144
40	5,23	0,23	0,0529
41	4,87	-0,13	0,0169
42	4,95	-0,05	0,0025
43	4,79	-0,21	0,0441
44	5,19	0,19	0,0361
45	5,03	0,03	0,0009
46	4,98	-0,02	0,0004
47	5,01	0,01	0,0001
48	5,04	0,04	0,0016
49	4,99	-0,01	0,0001
50	4,97	-0,03	0,0009
	⟨t⟩𝑁 = 5,00 с	0,00 C	𝜎𝑁 = 0,23 с 𝜌max = 1,75 с-1

8. 
   Расчет результатов косвенных измерений (таблицы, примеры расчетов).
   

Таблица 2: Данные для построения гистограммы

Границы интервалов, c	Δ𝑁	Δ𝑁 , c-1 𝑁Δt	t, c	𝜌, c-1
4,55	5	0,67	0,45	4,63
4,7
4,7	7	1,07	1,08	4,78
4,85
4,85	15	2,00	1,66	4,93
5
5	12	1,60	1,66	5,08
5,15
5,15	7	0,93	1,08	5,23
5,3
5,3	3	0,40	0,45	5,38
5,45
5,45	0	0,00	0,12	5,53
5,6
5,6	0	0,00	0,02	5,68
5,75
5,75	1	0,13	0,00	5,83
5,9

Таблица 3: Стандартные доверительные интервалы

	Интервал, c		/\ 𝑁	/\𝑁 𝑁		𝑃
	от	до
⟨t⟩𝑁 ± 𝜎𝑁	4,77	5,23	37	0,74	0,683
⟨t⟩𝑁 ± 2𝜎𝑁	4,54	5,46	49	0,98	0,954
⟨t⟩𝑁 ± 3𝜎𝑁	4,32	5,68	49	0,98	0,997

9. Расчет погрешностей измерений (для прямых и косвенных измерений).

1. 
   Cреднеквадратичное отклонение среднего значения: 𝜎 = 0,03
   

2. 
   Tабличное значение коэффициента Стьюдента t_𝛼,𝑁 для доверительной вероятности 𝛼 = 0,95: t_𝛼,𝑁 = 2,009575
   
3. 
   Доверительный интервал для измеряемого в работе промежутка времени: /\ t = 0,06
   

10. Графики.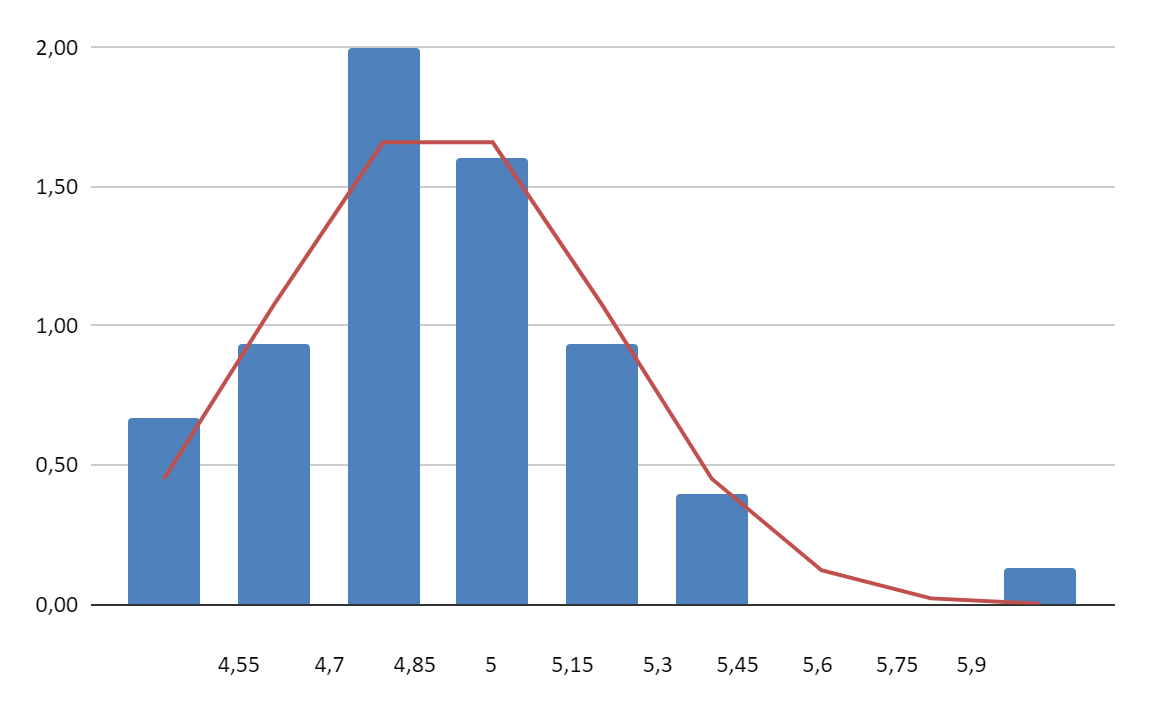


Рис. 1. Гистограмма и функция Гаусса
11. Результаты работы, их анализ и выводы на его основе.
Мы провести многократные измерения определенного интервала времени, с помощью специаьных программ для обработки табличных данных мы выполнили необходимые расчеты для постоения гистограммы и функции и постоили их. После сравнения гистограммы с графиком функции Гаусса с такими же как и у экспериментального распределения средним значением и дисперсией мы обнаружили что функция отражает общие закономерности гистограммы и лишь обозначает их немного плавнее. Также было обнаружено, что существует незначительная разница между вероятностями при условии реализации нормального распределения случайной величины в стандартных интервалах и эксепреснтальными вероятностями тех же интервалах для реальных условий.

12. Дополнительные задания.
Ответить на контрольные вопросы.

1. Являются ли, по вашему мнению, случайными следующие физические величины:

– плотность алмаза при 20∘𝐶

– напряжение сети

– сопротивление резистора, взятого наугад из партии с одним и тем же номинальным сопротивлением

– число молекул в 1см3 при нормальных условиях?

Приведите другие примеры случайных и неслучайных физических величин.

2. Изучая распределение ЭДС партии электрических батареек, студент использовал цифровой вольтметр. После нескольких измерений получились такие результаты (в вольтах): 1,50; 1,49; 1,50; 1,50; 1,49. Имеет ли смысл продолжать измерения? Что бы вы изменили в методике этого эксперимента?

3. При обработке результатов измерений емкости партии конденсаторов получено: 𝐶 = 1,1 мкФ, 𝜎 = 0,1 мкФ. Если взять коробку со 100 конденсаторами из этой партии, то сколько среди них можно ожидать конденсаторов с емкостью меньше 1 мкФ? больше 1,3 мкФ?
13. Выполнение дополнительных заданий.

1. 
   Плотность алмаза при 20∘𝐶 и число молекул в 1см3 при нормальных условиях - величины неслучайные и имеют постоянное значение. Напряжение сети
   

и сопротивление резистора, взятого наугад, относятся к величинам случайным.

Примеры неслучайных физических величин: постоянная Авогадро и масса покоя электрона. К случайных физическим величинам можно отнести: скорость электрона, вылетающего из нагретого катода электронной лампы, сила света, проникающего на дно водоема.

2. 
   Для того, чтобы дальнейшее измерение результатов имело смысл необходимо использовать измерительный прибор с более мелкой ценой делений и более высокой чувствительностью.
   

3. 
   Если допустить, что вероятности, по которым мы делаем выводы, существуют при условии реализации нормального распределения случайной величины, то тогда количесво конденсаторов с емкостью
   

меньше 1мкФ будет: (100-68,3)/2 = 15,85, т.е. 16 штук

больше 1,3мкФ: (100-95,4)/2 = 2,3, т.е 3 штуки
14. Замечания преподавателя