24 Расчет трубопроводов. Гидравлический расчет трубопроводов
 Скачать 0.78 Mb.
|
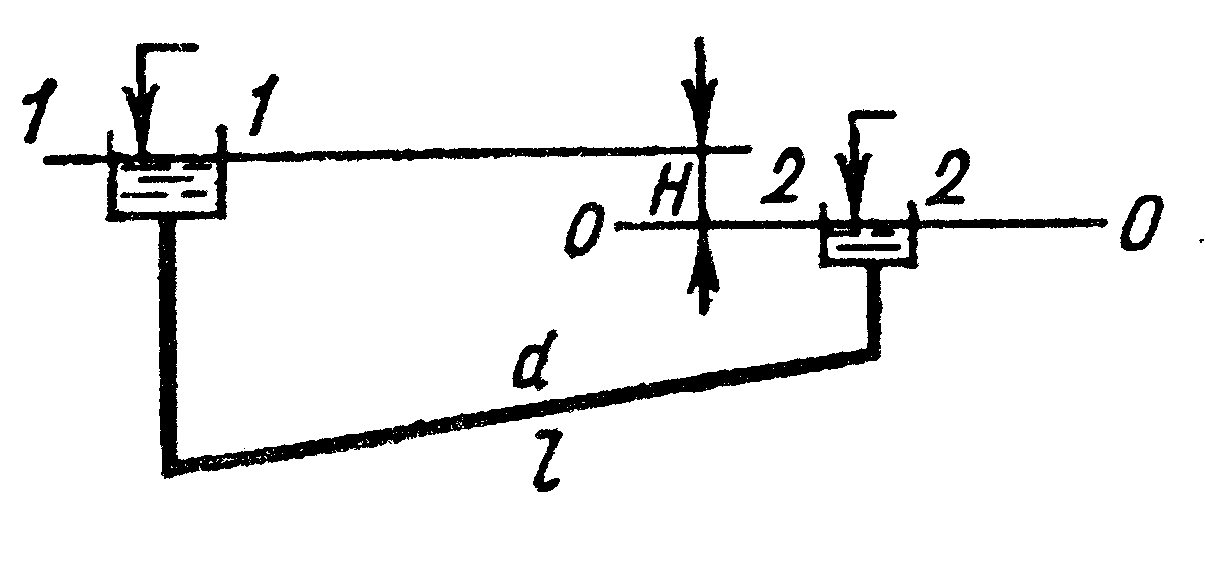
Гидравлический расчет трубопроводовРазличные способы расчета потерьРассматривается равномерное напорное движение жидкости в круглой трубе. При равномерном движении форма и площадь живого сечения, средняя скорость потока и эпюра скоростей по длине не изменяются. В этих условиях живое сечение характеризуется одним линейным размером – диаметром. Напомним:  .Общая формула для потерь напора по длине имеет вид  .Для круглых труб  .Это установленная экспериментально формула Дарси-Вейсбаха. Безразмерный коэффициент  называют коэффициентом гидравлического трения или коэффициентом Дарси. Коэффициент гидравлического трения зависит от относительной шероховатости трубопровода и числа Re.  . Для нахождения существуют эмпирические формулы (режимы ламинарный – переходный –турбулентный; область гидравлически гладких труб, доквадратичная область, квадратичная область).При равномерном движении жидкости средняя скорость потока, не изменяющаяся по длине из формулы равна  . Обозначим  .Коэффициент  называют коэффициентом Шези. Вспомним, что гидравлический уклон  и получим формулу Шези для средней скорости при равномерном движении  , где  .Потери напора по длине с учетом коэффициента Шези  .Коэффициент Шези в отличие от безразмерного коэффициента Дарси имеет размерность  . В справочниках приводятся таблицы значений коэффициента Шези для трубопроводов различного диаметра и различной шероховатости. Существует много эмпирических формул для расчета коэффициента Шези.Зная формулу для средней скорости потока получим формулу Шези для расхода при равномерном движении  .При расчете трубопровода обычно составляют уравнение Бернулли для потока вязкой жидкости. Пренебрегая местными потерями и скоростными напорами, получаем  .Вспомним, что гидравлический уклон , откуда  . Подставим найденное значение гидравлического уклона в формулу Шези для скорости потока  . Решаем уравнение относительно напора  . Заметим на будущее, что напор пропорционален квадрату скорости.Запишем формулу Шези для расхода при равномерном движении  .Объединим параметры, зависящие от диаметра трубопровода, представим их виде так называемой расходной характеристики трубопровода (модуля расхода)  .Расходная характеристика  представляет собой расход в данной трубе при гидравлическом уклоне, равном единице. Тогда расход  , напор  .При этом расход  и расходная характеристика должны быть выражены в одних и тех же единицах. В таблицах для гидравлических расчетов приводятся значения расходной характеристики для трубопроводов различного диаметра с различной относительной шероховатостью. На этой основе производится расчет трубопроводов «с использованием таблиц».Получим значение  расчетным путем. Гидравлический уклон равен 1, значит потери равны длине  . Потери по длине  . Отсюда  .   ;  . В квадратичной области турбулентного режима  Замечание. При равномерном движении гидравлический и пьезометрический уклоны равны. Пренебрегая скоростным напором, получим, что линия полного напора и пьезометрическая лини совпадают. Классификация трубопроводовПростой трубопровод – трубопровод, не имеющий ответвлений и состоящий из труб одинакового диаметра, выполненных из одного материала. Приведем два примера простых трубопроводов.
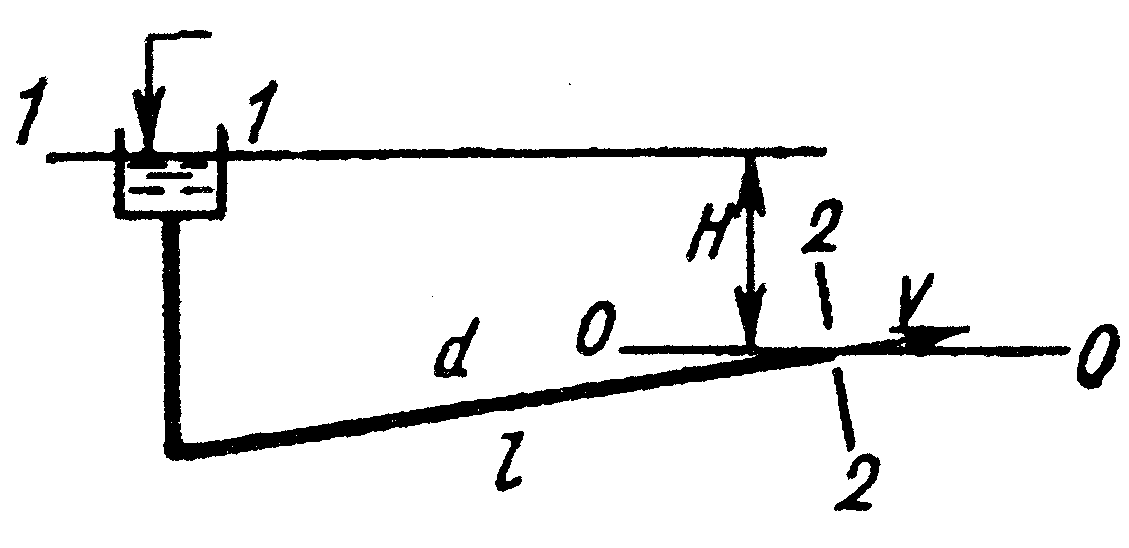
Движение жидкости в трубе обусловлено напором  , равным разности напоров в резурвуаре-питателе и приемнике или разности напоров в резервуаре питателе и в струе на выходе из трубы, если резервуар-приемник отсутствует. Если указанная разность напоров не изменяется во времени, то движение установившееся. Мы рассматриваем расчет только трубопроводов с установившимся движением.Потери напора в трубопроводе можно рассматривать как сумму потерь на трение по длине трубопровода и потерь в местных сопротивлениях  .По соотношению потерь по длине и в местных сопротивлениях в общей величине потерь трубопроводы делятся на гидравлически короткие и гидравлически длинные. В гидравлически длинном (или просто длинном) трубопроводе потери напора по длине настолько превышают местные потери (и скоростной напор), что местные потери не вычисляют, а принимают как некоторую часть потерь по длине. Практически при расчете длинных трубопроводов находят потери напора по длине  , а затем суммарные местные потери напора учитывают, увеличивая найденное значение на  %.  .В гидравлически коротком трубопроводе потери напора по длине и местные потери сопоставимы по значению. При гидравлическом расчете коротких трубопроводов учитывают как местные потери напора, так и потери по длине, а в балансе напоров учитывают скоростные напоры в сечениях потока. Классификация задач расчета трубопроводовПри расчете простого трубопровода необходимо установить связь следующих характеристик
Задачи по расчету трубопроводов подразделяются на задачи проектирования и задачи эксплуатации. Полагается, что длина трубопровода во всех случаях известна. Задачи проектирования : определение диаметра трубопровода, напора или давления на одном из его концов при заданной скорости жидкости в трубе или ее расходе. Задачи эксплуатации : определение эксплуатационных характеристик (расход, скорость жидкости) готового (существующего в натуре или в проекте) трубопровода с известным диаметром и шероховатостью, а также с определенными напорами (давлениями) на концах трубы. По методу расчета подразделяют задачи прямые и обратные. При решении прямых задач искомые величины находятся по расчетным формулам в явном виде. В обратных задачах искомую величину в явном виде выразить не удается, решение находят с помощью итерационных процедур. Расчетные формулыРасполагаемый напор равен потерям. Потери складываются из потерь по длине и потерь в местных сопротивлениях. Потери по длине определяются по формуле Дарси-Вейсбаха (первая водопроводная формула). Потери в местных сопротивлениях суммируются по всем местным сопротивлениям и зависят от коэффициента потерь в каждом из них  . Получаем формулу, которая связывает среднюю скорость и располагаемый напор. ;  ;  ;  ;  При расчете трубопровода «с использованием таблиц»  , где расходная характеристика берется из таблиц.По определению средняя скорость потока  . Очевидно  Число Рейнольдса  или  . Значения динамической вязкости и плотности или кинематической вязкости жидкости при данной температуре известны.Коэффициент сопротивления трения ( коэффициент Дарси ) определяется по эмпирическим формулам и зависит от Re и абсолютной эквивалентной шероховатости  , которая для данного вида труб (материала, исполнения) известна (задается в справочниках, для новых стальных труб  =0,2 мм, для старых водопроводных =1,5 мм).Применение тех или иных эмпирических формул определяется режимом движения жидкости (числом Re ), а при турбулентном режиме областью сопротивления. I – ламинарный режим движения Границы  Формула  II – переходный режим движения Границы  Формула  III – область гладких труб Границы:  . Формула Блазиуса  IV – область доквадратичного сопротивления (или переходная) Границы :  . Формула Альтшуля  V- область квадратичного сопротивления (или шероховатых труб) Границы:  . Формула Шифринсона  Расчет простого трубопроводаЗадачи, чаще всего встречающиеся в практике, приведены ниже ( четыре параметра, два заданы, два оставшиеся определяются расчетом; число различных сочетаний из 4 по 2 равно 6)
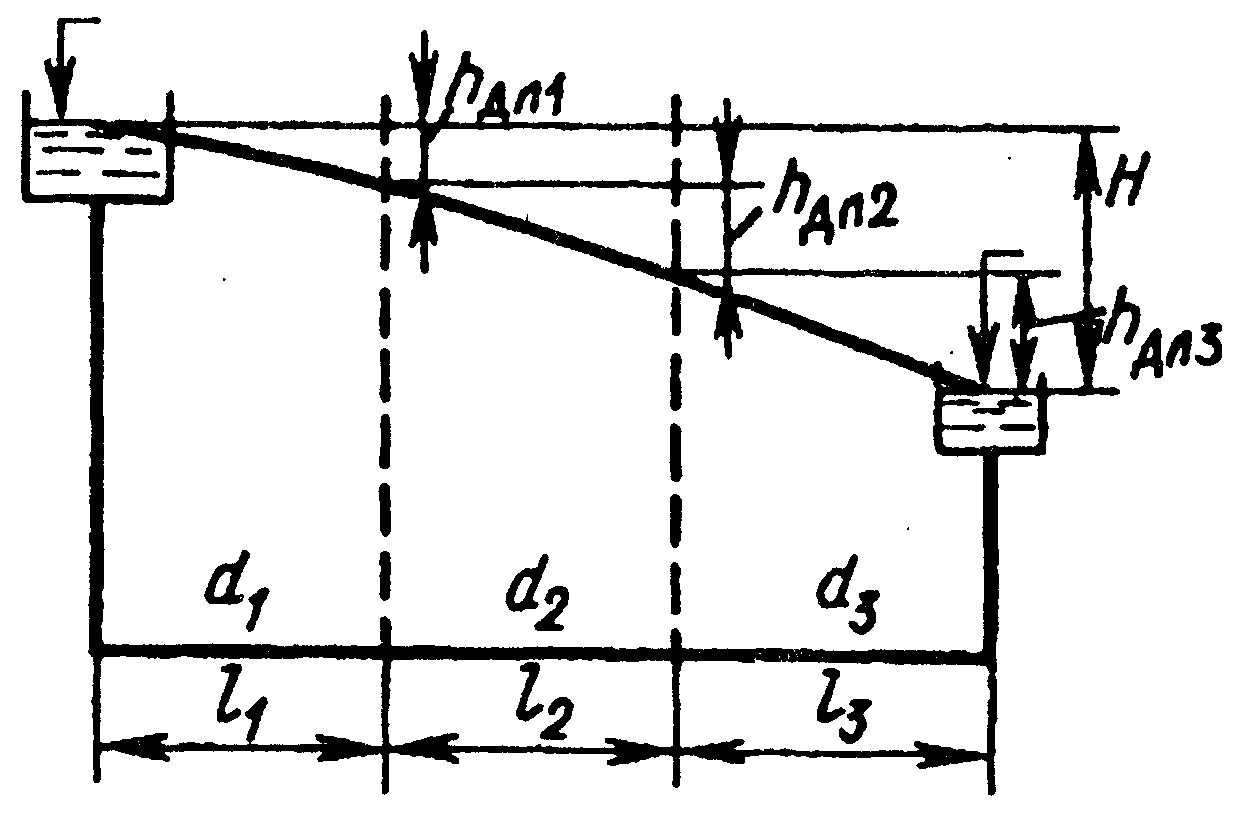
Решение прямых задач начинается с нахождения числа Re. 1.  и  => Re2. и => => Re3. и => => ReДальнейший алгоритм расчета одинаков Re => => .При решении обратных задач «без использования таблиц» не удается получить аналитического решения. Следует применить итерационную процедуру, т.е. задаться искомым значением, а затем уточнять его. Выражение для располагаемого напора следует решить относительно скорости 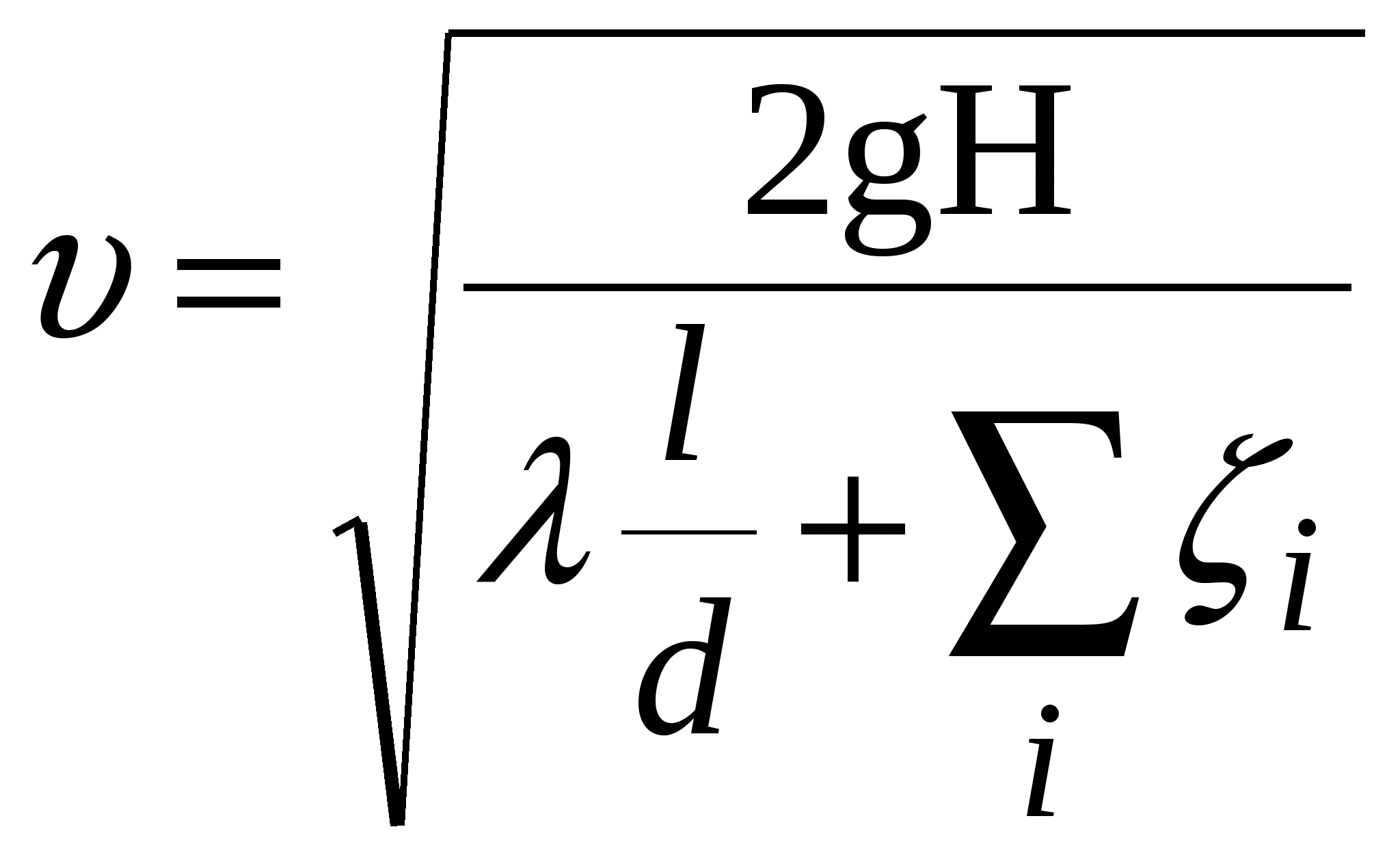 Задача 4 (подбираем скорость) : , => задаемся => Re => =>  (больше/меньше заданного) =>новое .Задача 5 (подбираем диаметр): , => задаемся => => Re => =>  (больше/меньше заданного) => новое .Задача 6 (подбираем диаметр): , => задаемся => Re => => (больше/меньше заданного) => новое .В учебных целях рекомендуется сопровождать решение графической иллюстрацией процесса последовательных приближений. Для этого по имеющимся расчетным данным следует изобразить следующие зависимости: Задача 4.  . Задачи 5 и 6.  Графоаналитический метод решения задач обратного типа состоит в следующем ( на примере задачи 4). Задаемся значением скорости , находим напор , который, разумеется, отличается от заданного в условии. Если полученное значение меньше заданного, то увеличиваем скорость, если больше, то уменьшаем. Повторяем расчет. Строим в масштабе зависимость . Для построения зависимости необходимо не менее 3-х точек. Из полученной графической зависимости находим значение , которому соответствует заданный напор . Производим проверку найденного значения.Последовательное соединение трубопроводовРассмотрим систему из последовательно соединенных длинных труб различных диаметров и длин. В общем случае материал труб может быть различным (различная шероховатость).
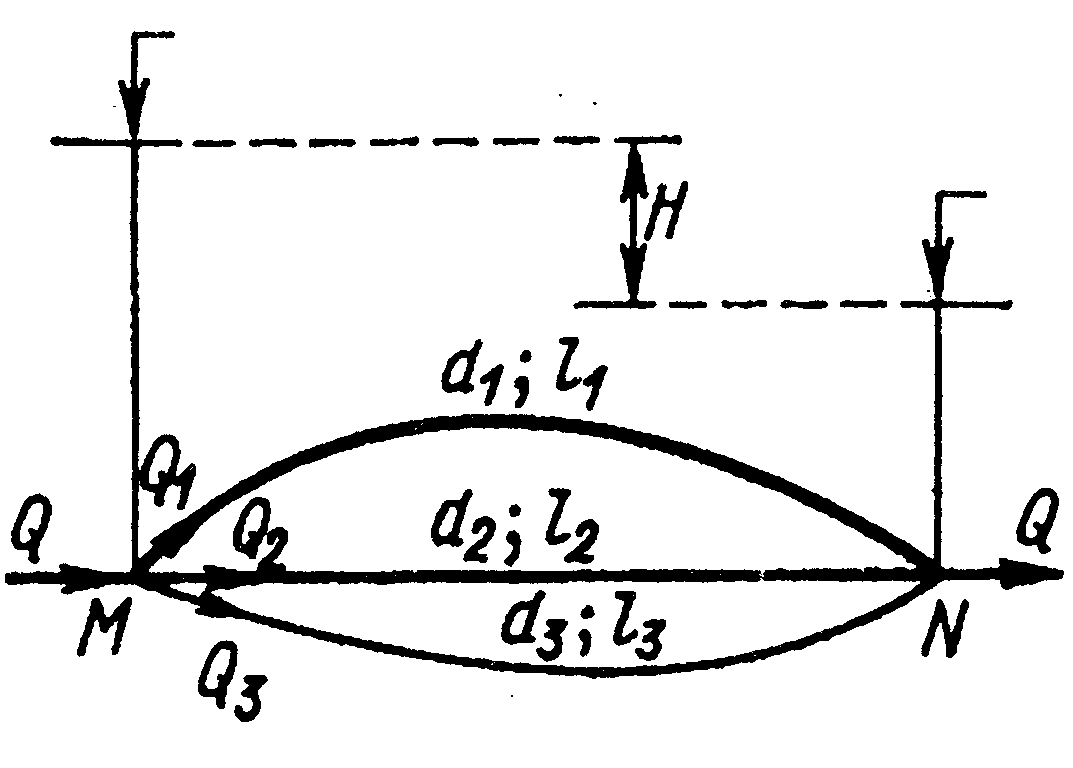
 , где i= 1, 2 … n – номер участка.Поскольку местными потерями пренебрегаем, напор  затрачивается на преодоление потерь напора по длине и будет равен сумме потерь напора на отдельных участках  Вывод. Для последовательного соединения расход одинаков, а напор равен сумме напоров. Аналогия – последовательное соединение сопротивлений, ток одинаков а напряжения суммируются. Параллельное соединение трубопроводовРассмотрим систему из параллельно соединенных длинных труб.
Расход, проходящий по любому участку  . Для всех участков имеем n уравнений для  . Сумма расходов на отдельных участках должна быть равна общему расходу, поступающему в систему параллельно соединенных трубопроводов в точке M и выходящему из системы в точке N. .Таким образом, имеем n+1уравнение, из которых может быть найден необходимый напор и расход в каждом из параллельных участков. Распределение расходов между участками заранее не известно. Поэтому все расходы выражают через какой-нибудь один, например через  . Имеем  , откуда  .Суммарный расход 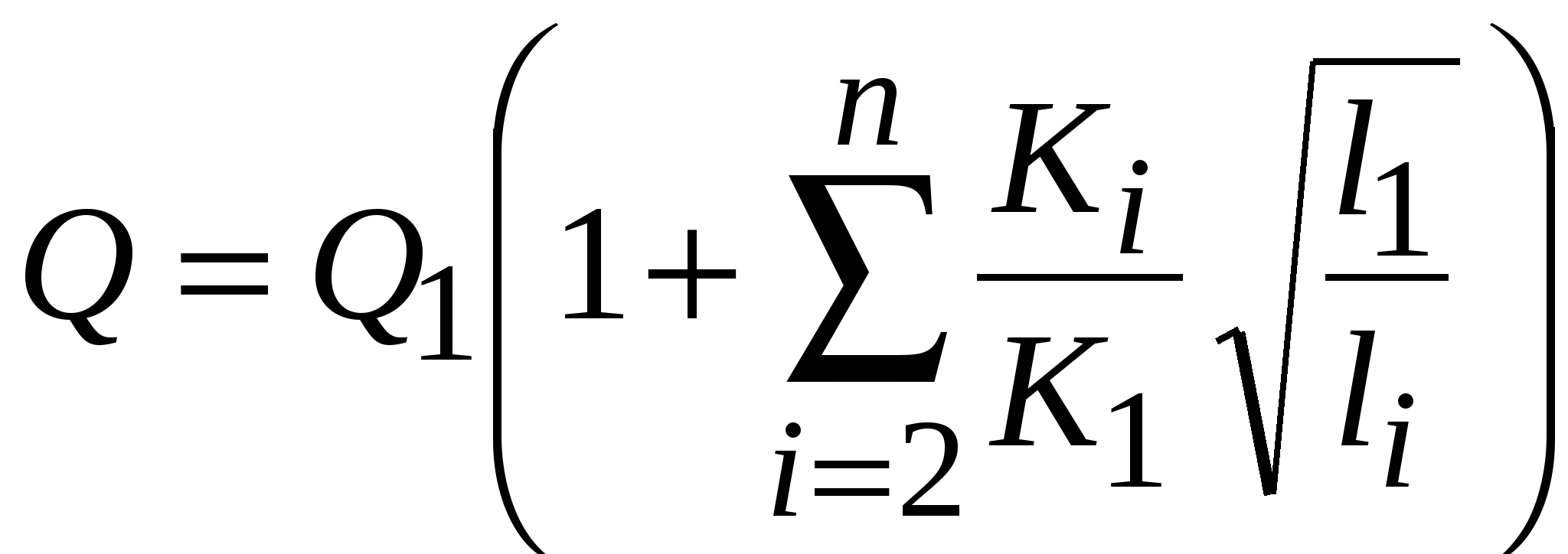 . Отсюда находим и все остальные.Вывод. Для параллельного соединения напор одинаков, а расход равен сумме расходов. Аналогия – параллельное соединение сопротивлений, напряжение одинаково, а токи суммируются. Расходная характеристика участка трубопровода
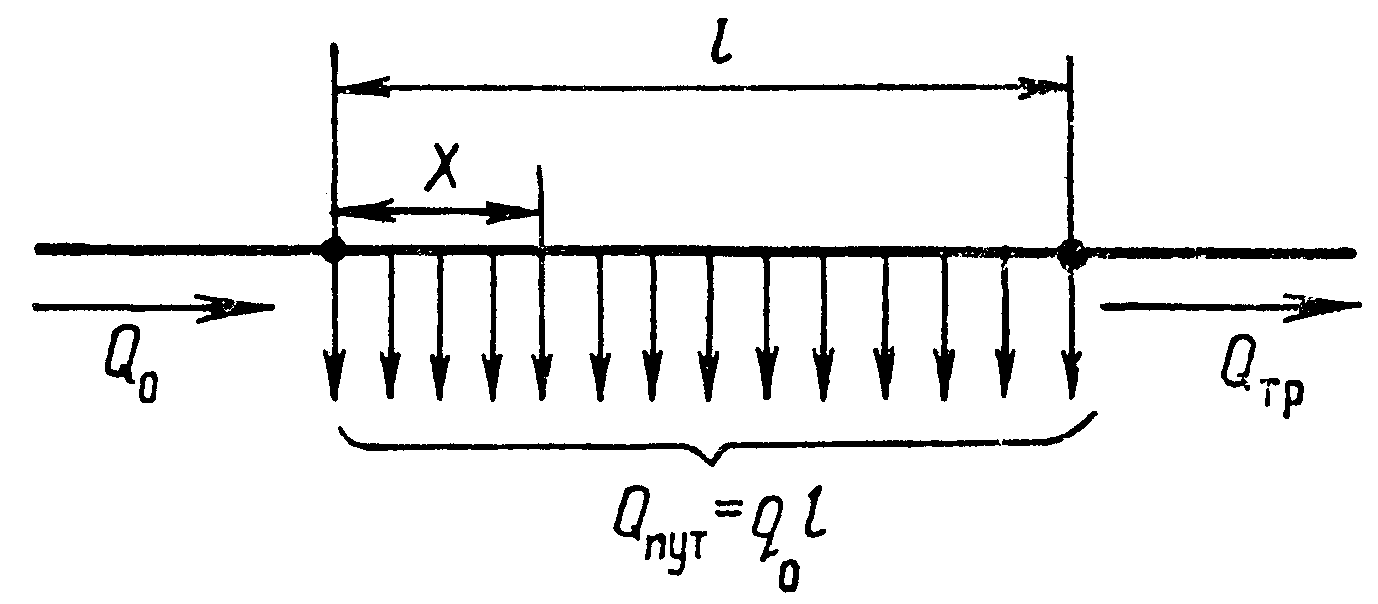
Расчет трубопровода с непрерывным изменением расхода по длинеЧасто встречаются случаи, когда по длине трубопровода происходит раздача некоторой части или всего расхода, причем отбор жидкости (воды) потребителями происходит в нескольких сечениях по длине трубопровода. К таким трубопроводам относятся городские и сельские водопроводы, поливные трубопроводы, подающие воду в каждую борозду через отверстия, трубопроводы различных технических систем, в том числе внутрипочвенного и капельного орошения. Собирающие трубопроводы (дренажные коллекторы) работают с увеличением расхода по длине. Трубопроводы с непрерывной равномерной раздачей воды вдоль пути характеризуются тем, что точки разбора находятся на одинаковом расстоянии друг от друга, а расходы разбора в этих точках одинаковы. При этом удельный путевой расход на единицу длины составляет  .
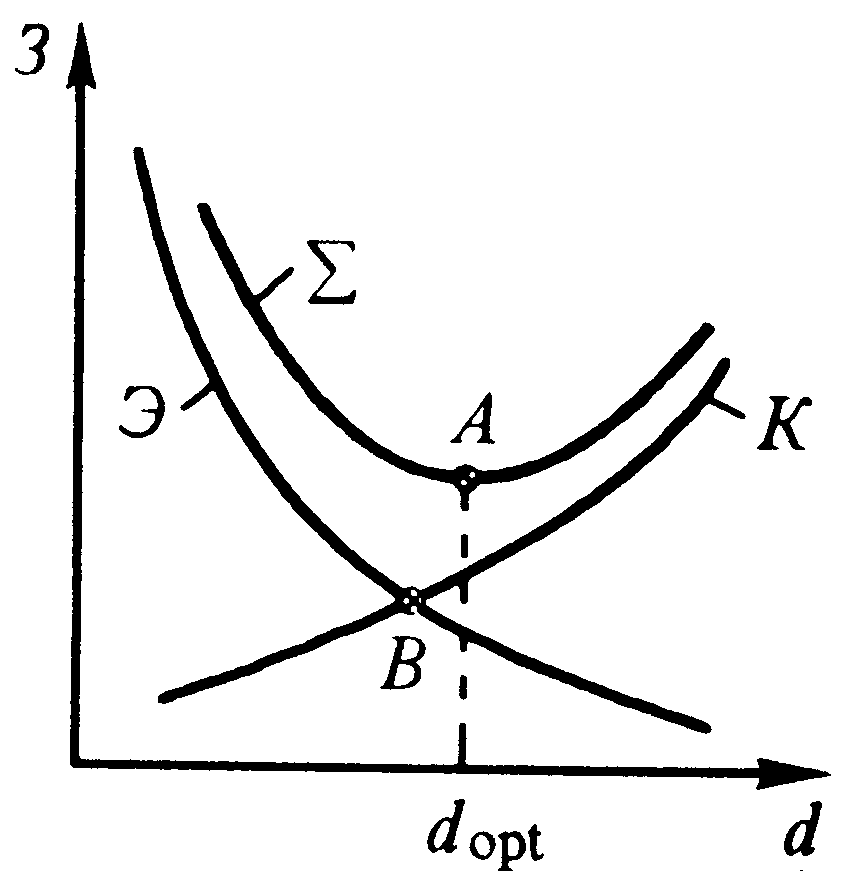
Определим потери напора  на таком участке.В любом сечении на расстоянии  от начала разбора расход  .Гидравлический уклон  , откуда  . Для нахождения потерь напора на длине  интегрируем полученное выражение в пределах от 0 до : Раскроем подынтегральное выражение1 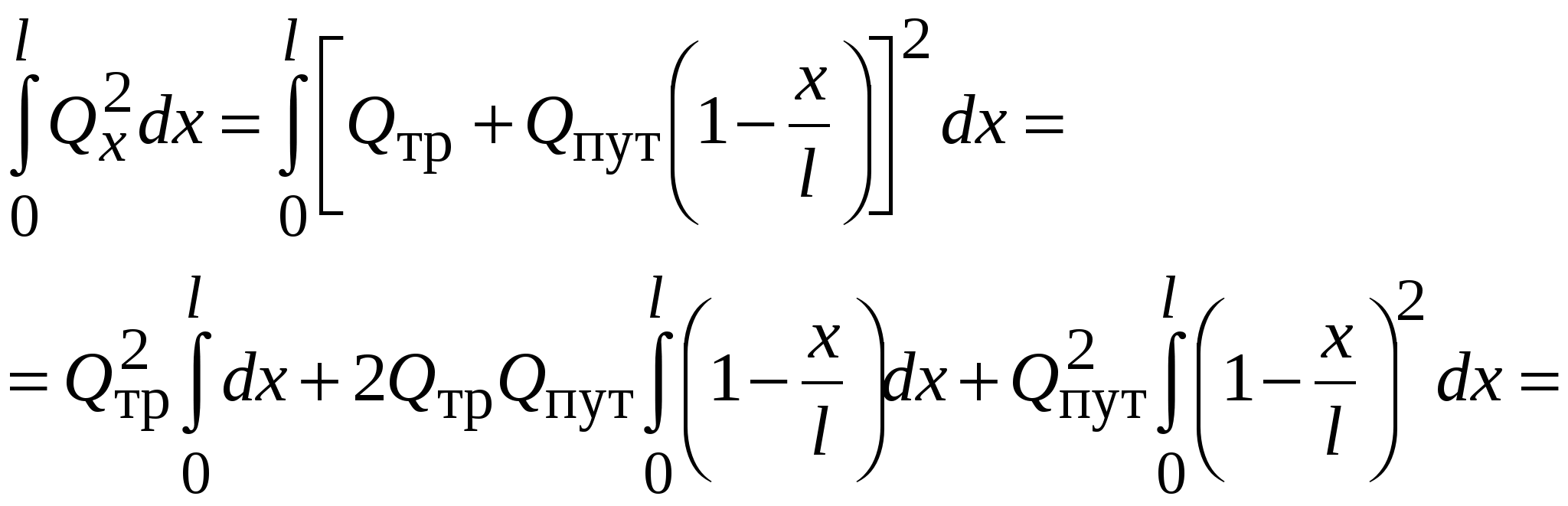   .Подставляем значение интеграла в формулу для потерь напора 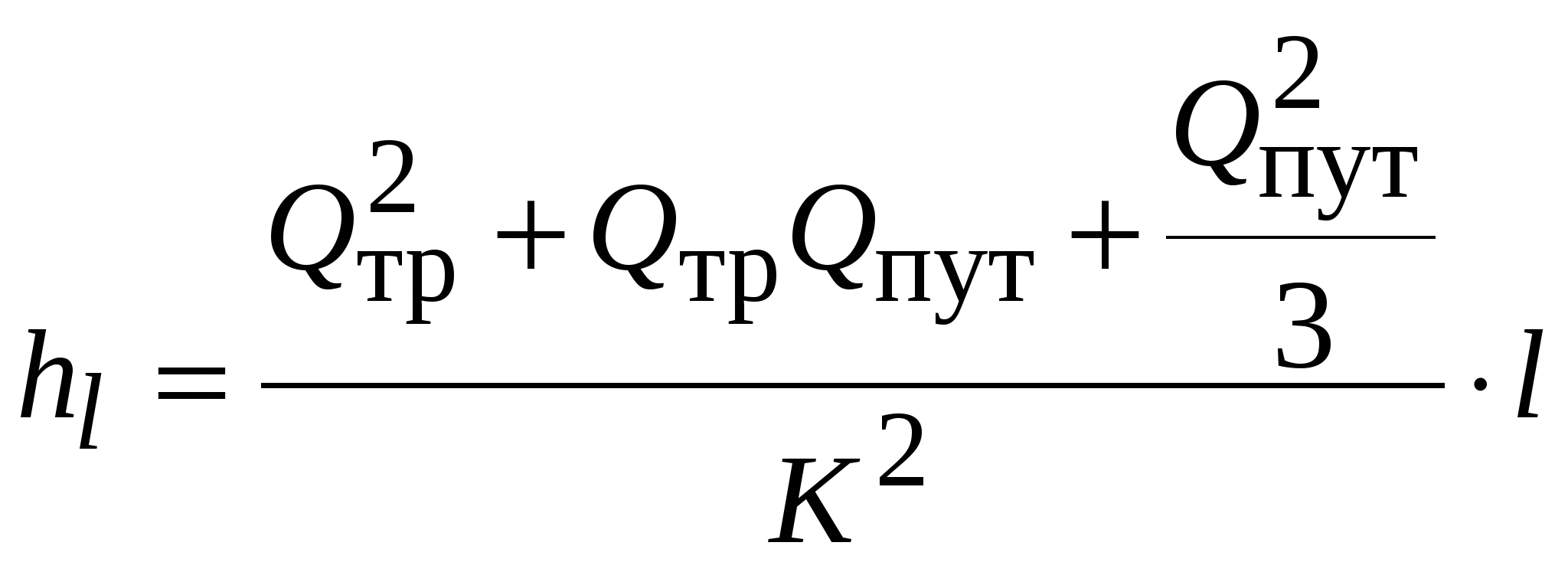 .Введем понятие расчетного расхода  Окончательно расчетная зависимость имеет вид  .Расчетный расход больше транзитного, но меньше полного расхода в начале трубопровода. В практических расчетах для упрощения принимают  .Оптимальные диаметр трубопровода и средняя скоростьНеобходимость определения диаметра трубопровода возникает в задачах проектирования. Один и тот же расход может быть подан через трубопровод большего диаметра с меньшими потерями напора или наоборот. Оптимальный диаметр трубопровода определяется по сопоставлению капитальных и эксплуатационных затрат.
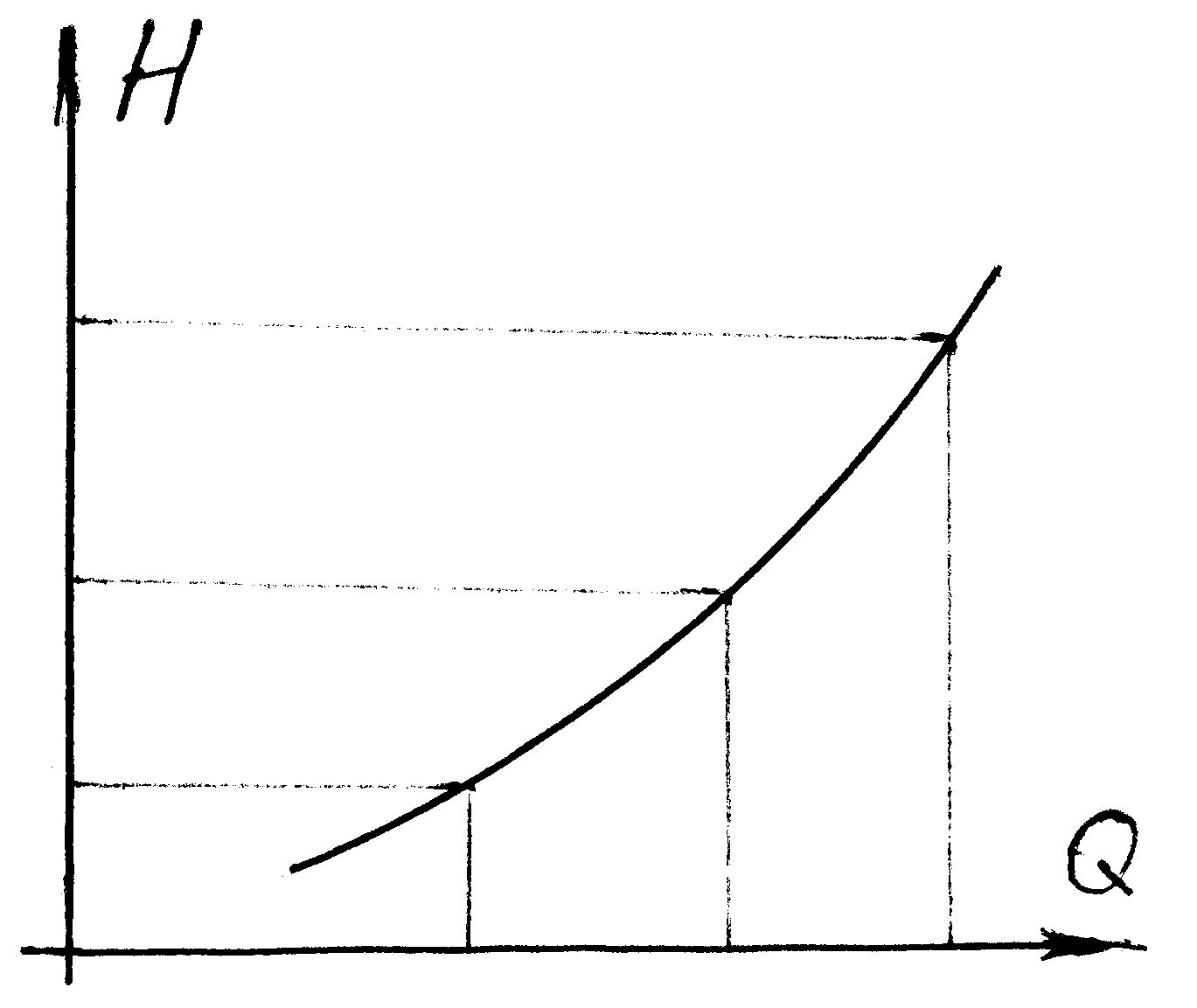
На рисунке минимуму кривой отвечает точка  ; значит следует подбирать трубопровод, близкий по диаметру к оптимальному:  .Заметим, что в учебниках иногда ошибочно определяют  как абсциссу точки  ; несмотря на возможную близость в каких-то случаях к , диаметр  , отвечающий равенству капитальных и эксплуатационных затрат, вообще говоря никакого интереса не представляет.Сравнение капитальных и эксплуатационных затрат не всегда возможно из-за отсутствия необходимой информации. На практике используют таблицу рекомендуемых предельных скоростей и предельных расходов (таблица приводится выборочно)
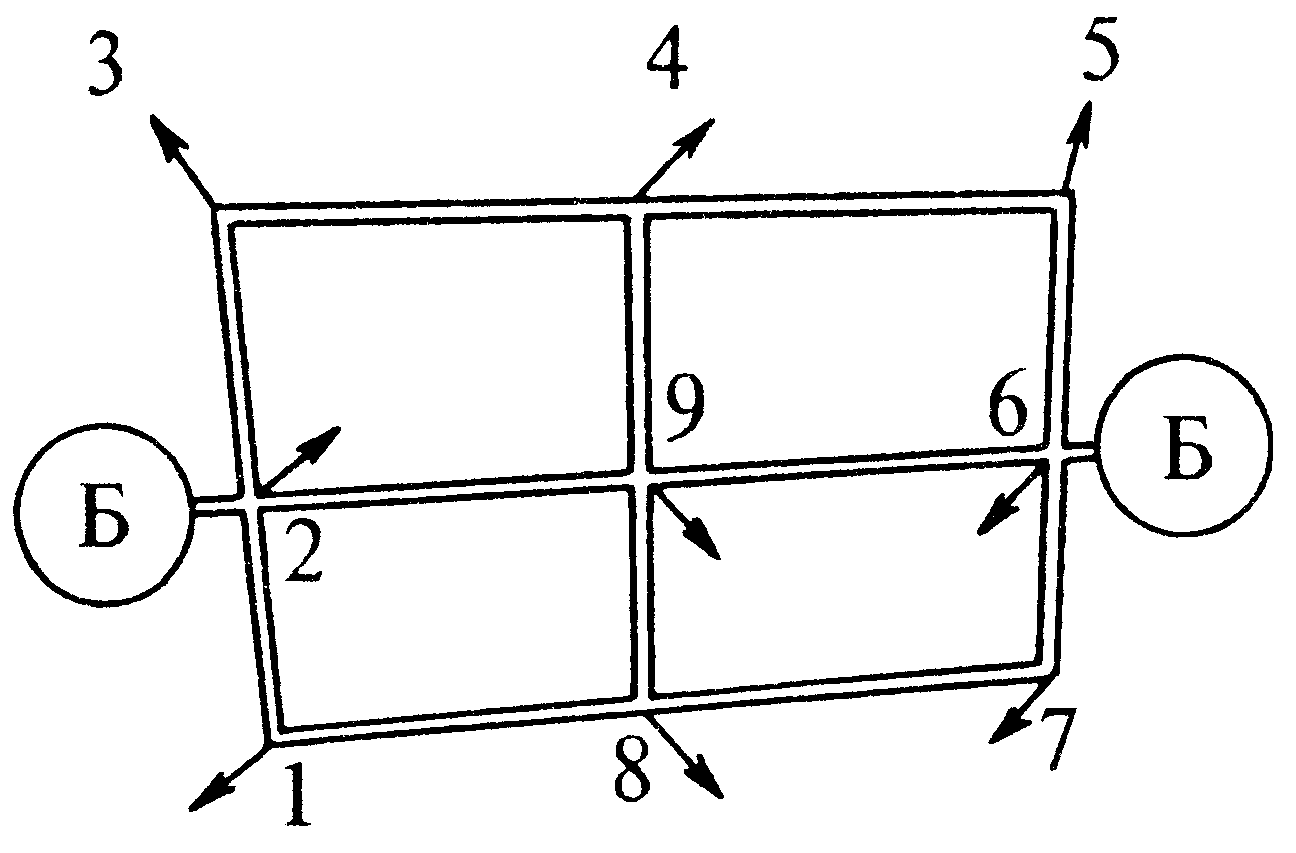
Таблица применима для стальных труб, прокладываемых в центральных и западных районах России. Для районов Сибири и Урала приведенные в таблице расходы и скорости увеличивают на 1015%. Для Южных районов СНГ уменьшают на 10%. Причины: в Сибири и на Урале более дешевая электроэнергия, но большие капиталовложения в строительство трубопроводов в связи с большой глубиной прокладки труб; в южных районах СНГ более дорогая электроэнергия, но меньше затраты на строительство. Кольцевые и тупиковые водопроводные сетиВодопроводные сети, по которым вода из водонапорной башни поступает к потребителям, делят на разветвленные (тупиковые) и кольцевые.
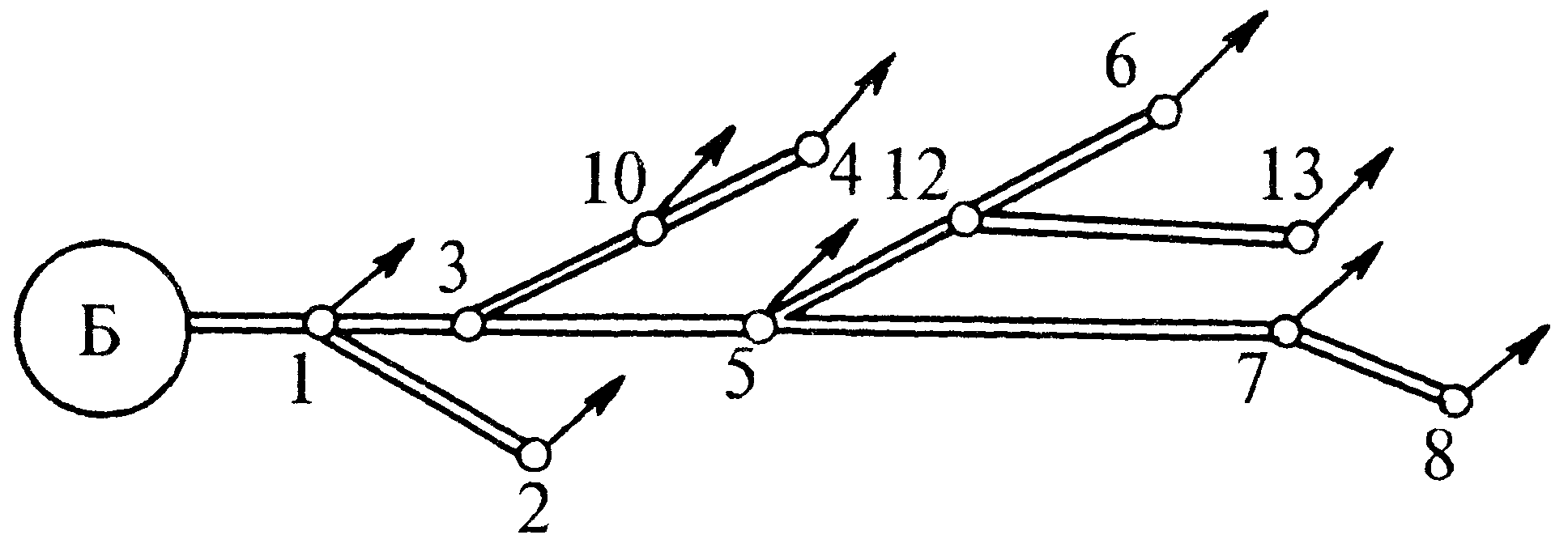
Кольцевая сеть позволяет осуществлять водоснабжение всех потребителей в случае аварии или ремонта отдельных участков водопроводной сети. При этом, конечно, потребности в воде будут удовлетворяться не полностью, а , например, на несколько часов в сутки, причем иногда обеспечиваются лишь нижние этажи зданий и т.п., но все же водоснабжение не буден отключено полностью на все время ремонта, что может произойти, если сеть тупиковая. Строительными нормами и правилами рекомендуется обеспечить пьезометрический напор не менее 10 м при одноэтажной застройке, добавляя 4 м на каждый этаж. Расчет разветвленного трубопровода.Определить расход жидкости, протекающей по разветвленному трубопроводу в пункты 1 и 2 (истечение в атмосферу). Напор в резервуаре постоянен и известен. Длины и диаметры отдельных участков трубопровода известны. Кинематическая вязкость жидкости и абсолютная эквивалентная шероховатость известны. Местными потерями напора и скоростным напором пренебречь.
Примечание.
Решение. В разветвленном трубопроводе сохраняется баланс расходов  .Неизвестны два расхода, третий находится по балансу. Потери в ветвях разветвляющейся части одинаковы, т.е.  . Располагаемый напор  . Потери в каждом трубопроводе рассчитываются по формуле Дарси-Вейсбаха  . Расход по участку  . Площади  известны. Тогда  .В первом приближении примем, что режим движения жидкости в трубопроводе турбулентный, квадратичная область сопротивления (в дальнейшем это утверждение будет уточнено). Коэффициент Дарси для каждого диаметра может быть определен по формуле Шифринсона 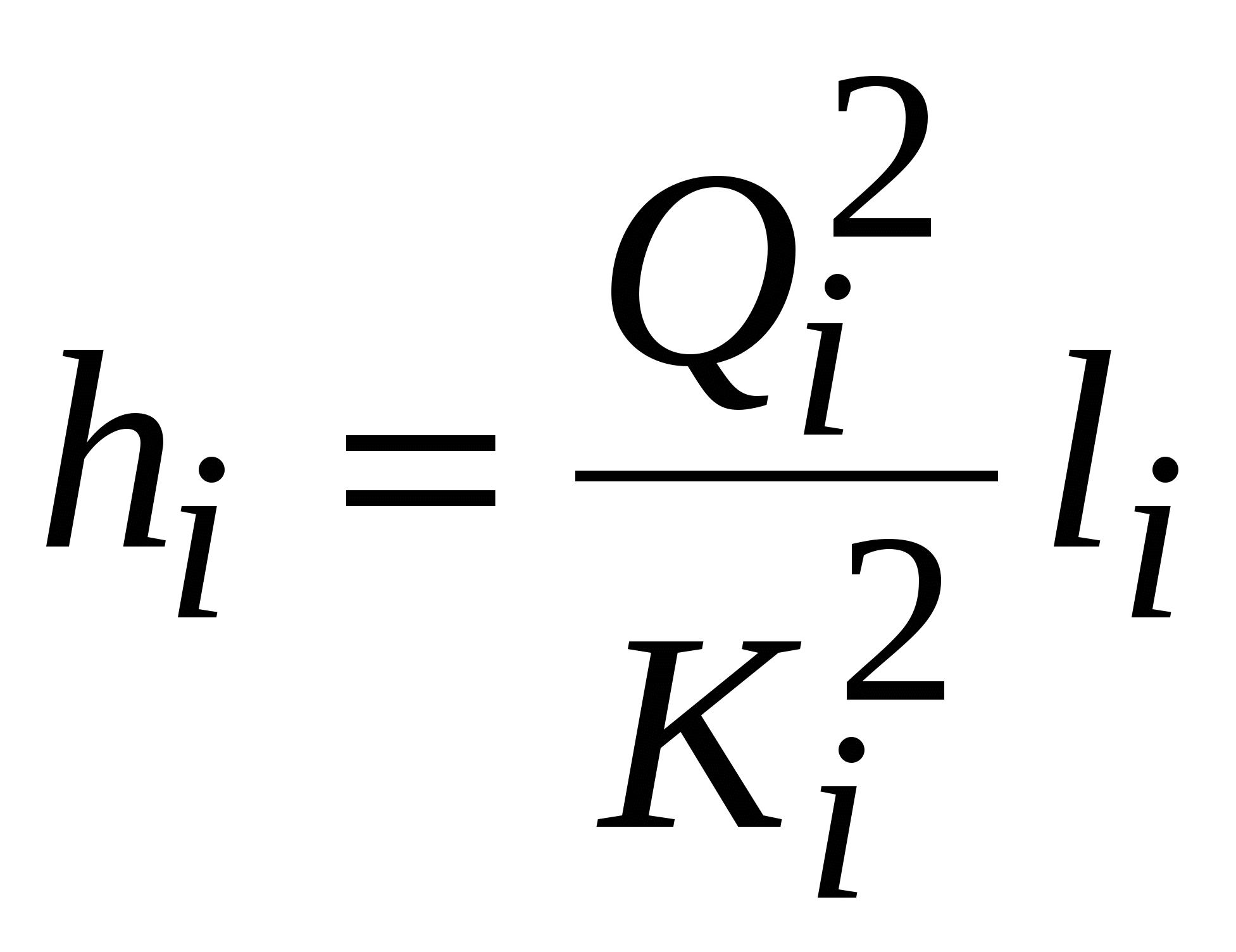 . Потери в каждом участке трубопровода могут найдены через его расходную характеристику, при чем последняя не берется из таблиц, а определяется аналитически.  . Здесь расходная характеристика  .Получим шесть уравнений с шестью неизвестными (расходы и потери напора в участках) 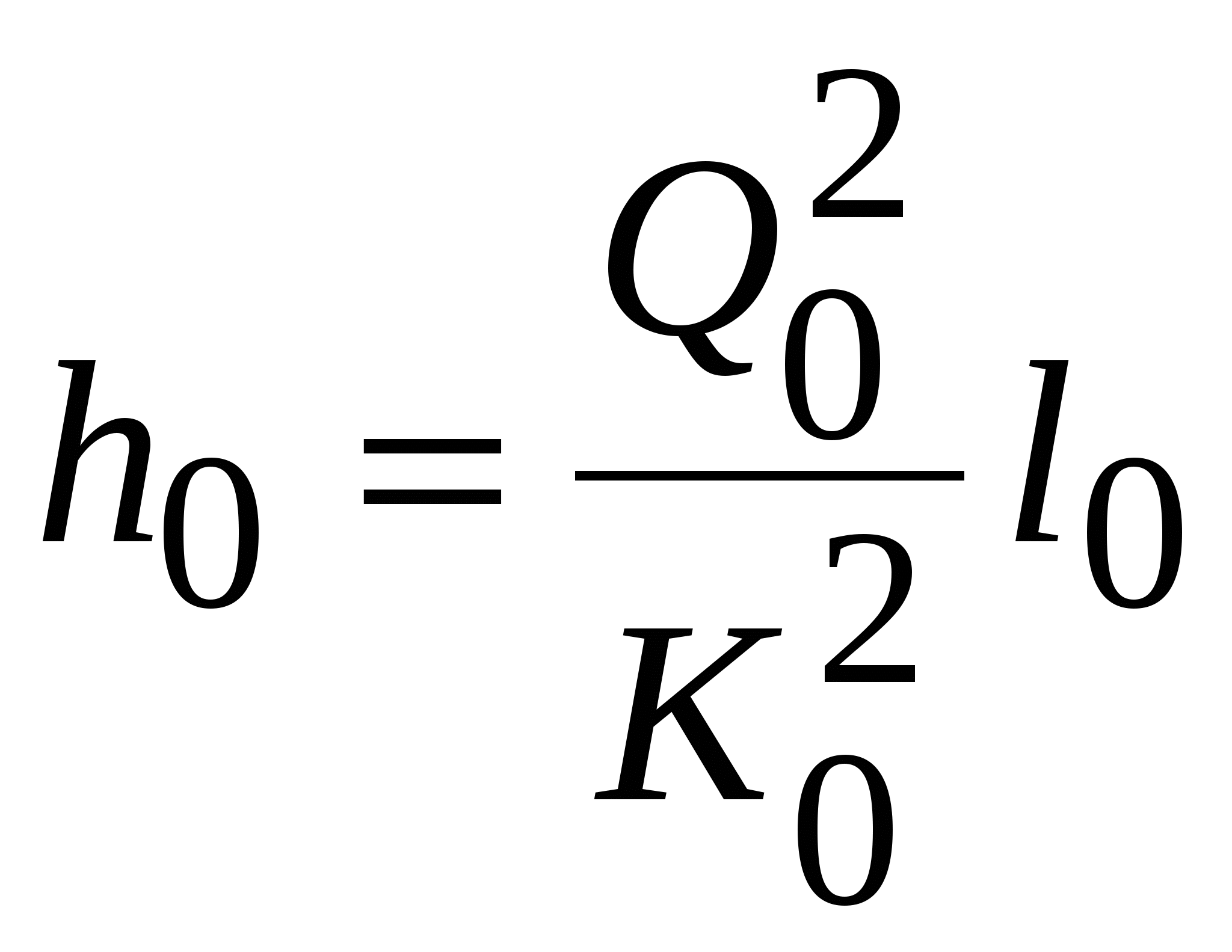 ,  ,  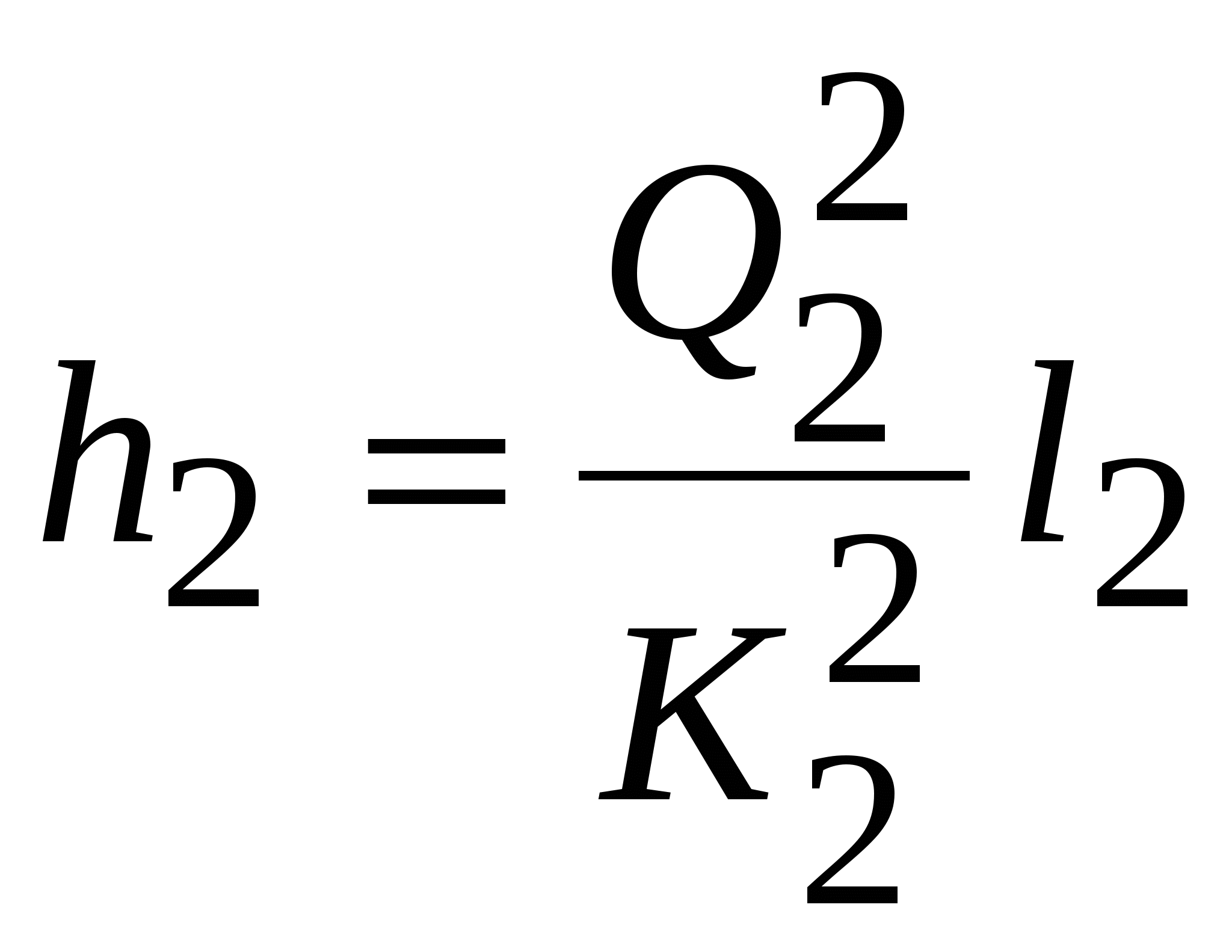, ,  ,  .Несложные алгебраические преобразования приводят к следующим результатам: 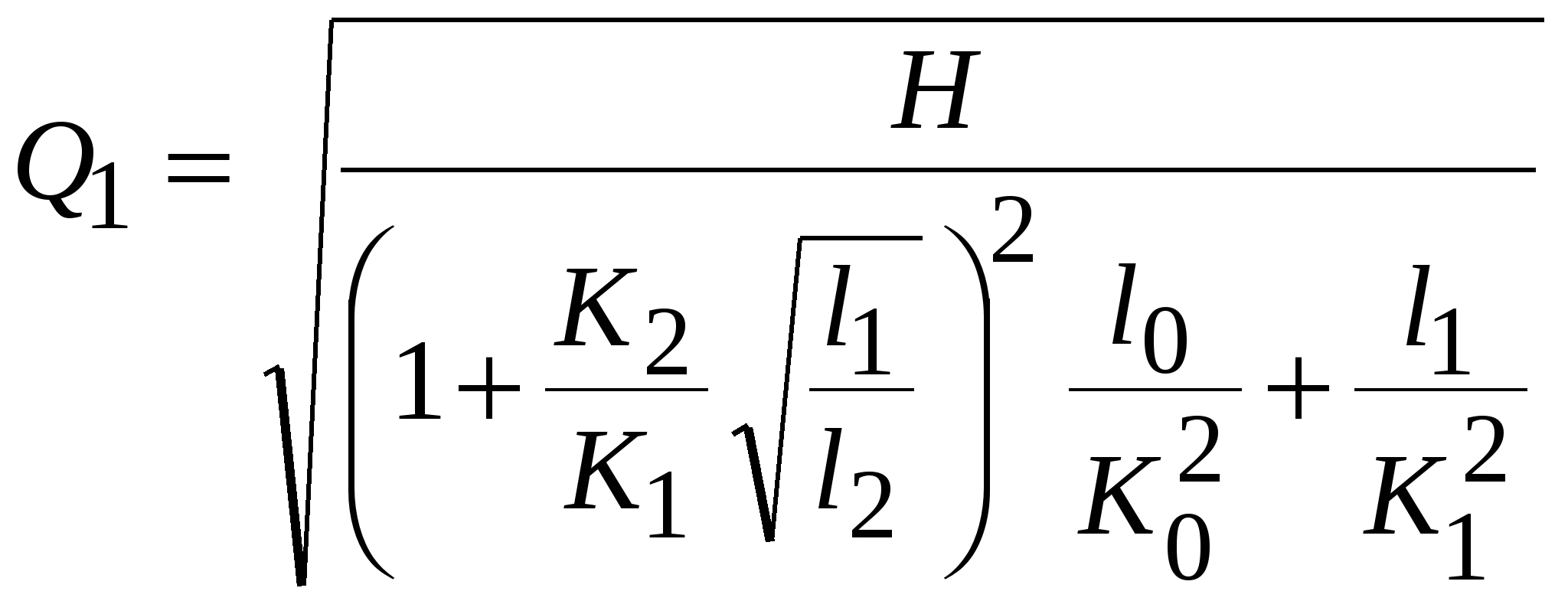  Уточнение полученных результатов производится в следующей последовательности. Находят средние скорости во всех участках трубопровода, числа Re. Определяют область гидравлического сопротивления, в которой работает каждый участок, и по соответствующим эмпирическим формулам (Блазиуса, Альтшуля, Шифринсона и др.) вычисляют значение коэффициента Дарси. Уточняют значения расходных характеристик участков  и вновь вычисляют расходы по участкам. Такой способ позволяет получить решение с любой требуемой точностью. Графоаналитический способ решения задачи. Задаются начальным приближением по скорости. Пусть, например 2 м/с по участку 1. Скорость по участку 2 определяют из простой пропорции (равенство потерь по длине при одинаковом коэффициенте Дарси.  .Находим расход по участкам и общий расход а также скорость на участке 0. На каждом участке находим число Re, определяем область сопротивления и по соответствующей формуле находим коэффициент Дарси. Вычисляем потери по длине на каждом участке.
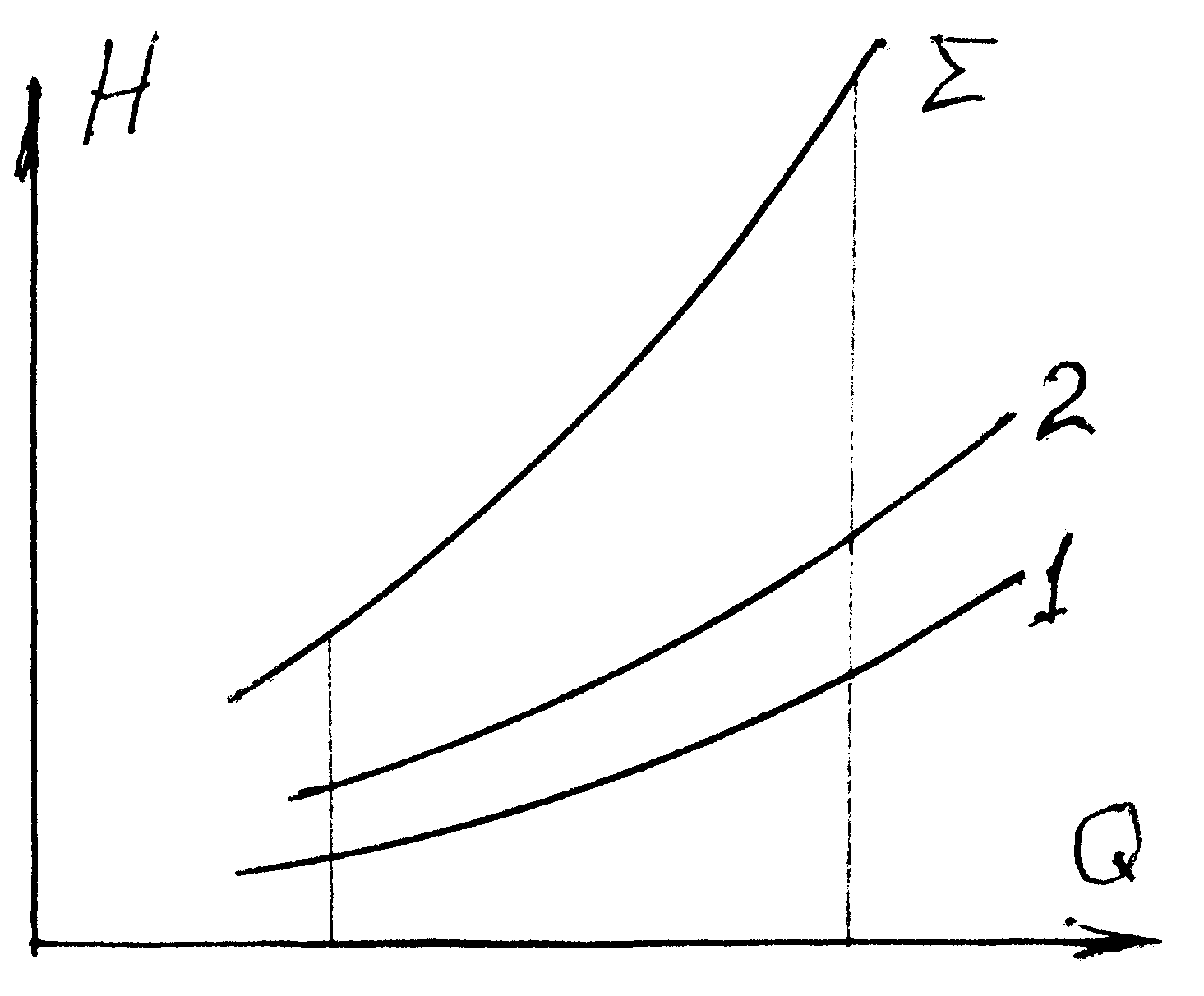
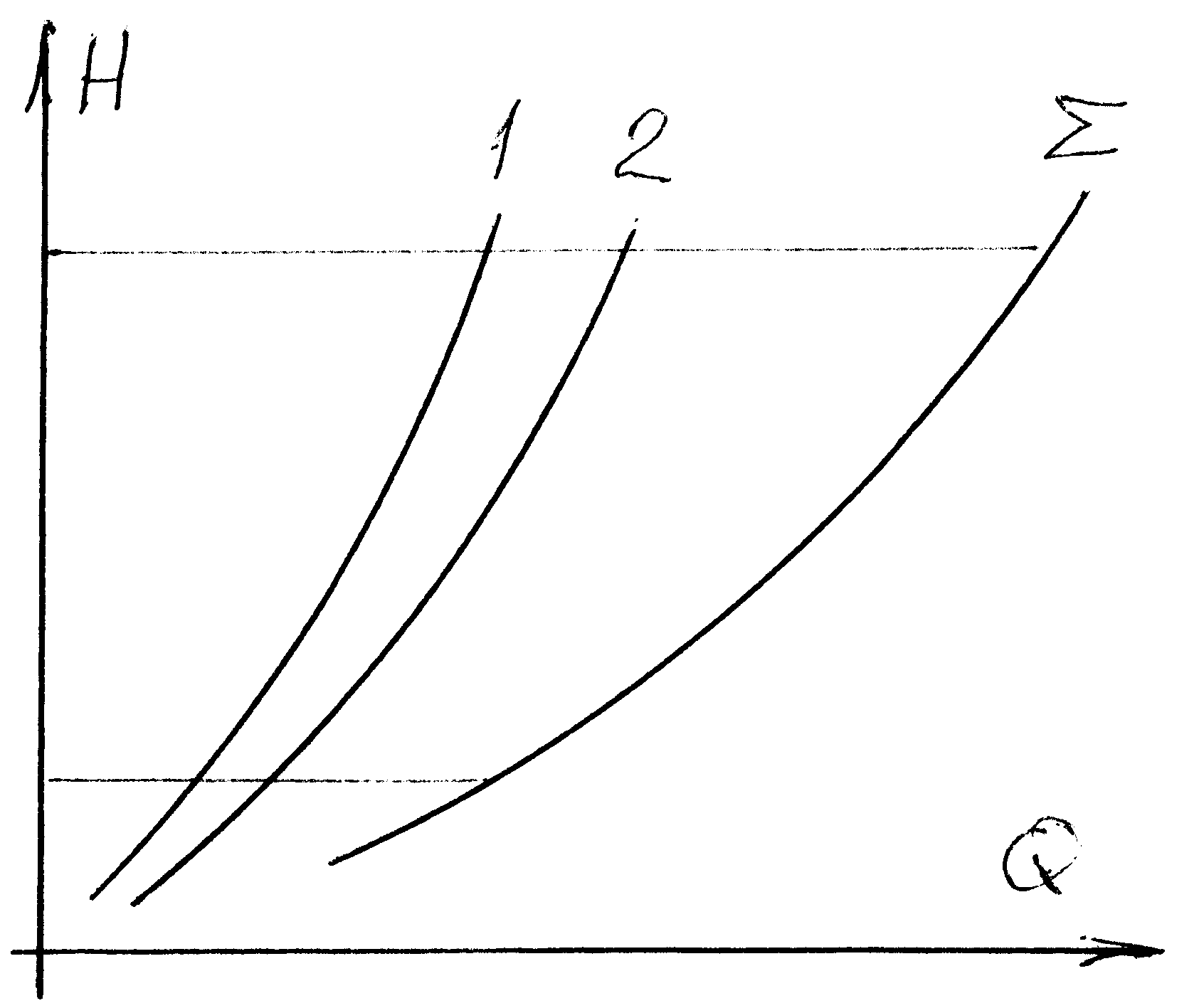
На одном графике строим расходные характеристики участков 1 и 2. Эти участки соединены параллельно, суммарная характеристика строится путем суммирования расходов при одинаковом напоре (кривая 1+2). На этом же графике строим характеристику участка 0. Этот участок соединен с участком 1+2 последовательно, суммарная характеристика всего трубопровода строится суммированием напоров при одинаковом расходе (кривая  ). По заданному суммарному напору  по кривой находим расход через весь трубопровод и через участок 0. (Линия -a-b-c- .) Точке b соответствует напор на участках 1 и 2, точке с напор на участке 0. Пересечение горизонтали через точку b с характеристиками трубопроводов 1 и 2 определяет расходы в них. (Линии b-d- иb-e- .)Рассмотренный графоаналитический способ расчета не дает точного решения, однако позволяет разработать алгоритм его нахождения с использованием средств вычислительной техники. 1 Напомним использованные сведения из математики. Квадрат суммы  . Квадрат разности  . Постоянные выносятся за знак интеграла. Интеграл суммы (разности) есть сумма (разность) интегралов. Табличные интегралы    |
называется расходной характеристикой участка трубопровода. Она может быть получена аналитически или с помощью таблиц. Как правило построение расходной характеристики производится по точкам. Задаются различными значениями расхода и находят потери напора на данном участке трубопровода. Строят зависимость
, поступающий к начальному сечению трубопровода, состоит из двух: 
, который разбирается по длине 
, проходящего через данный участок: 
, при этом 
.
