курсач ггд. Курсовой прект по ГГД. Гидравлический расчет участков линии нагнетания. Гидравлический расчет 7 участка

• Название: Гидравлический расчет участков линии нагнетания. Гидравлический расчет 7 участка
• Анкор: курсач ггд
• Дата: 20.10.2022
• Размер: 1.07 Mb.
• Имя файла: Курсовой прект по ГГД.docx
• Тип: Реферат; #743185

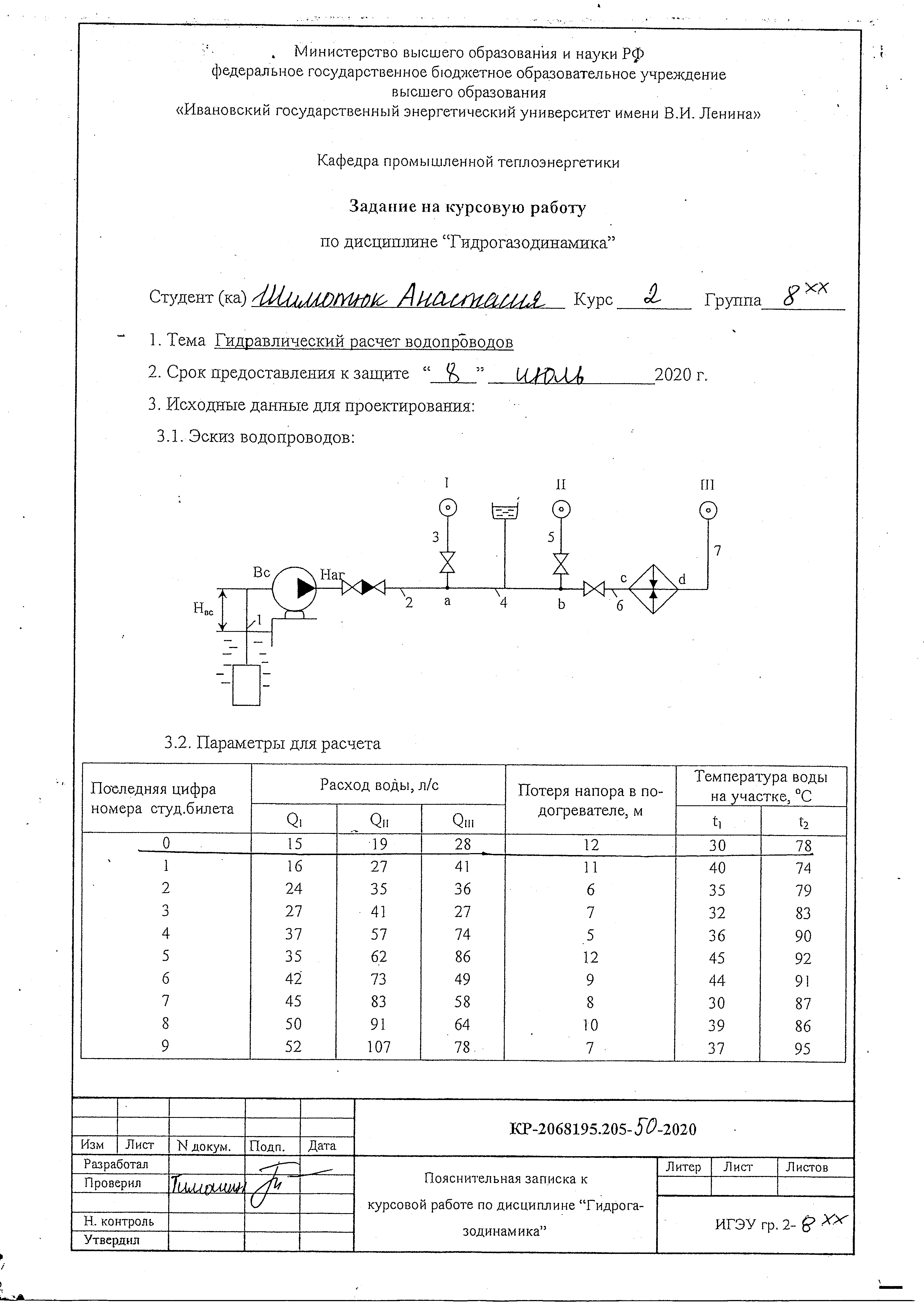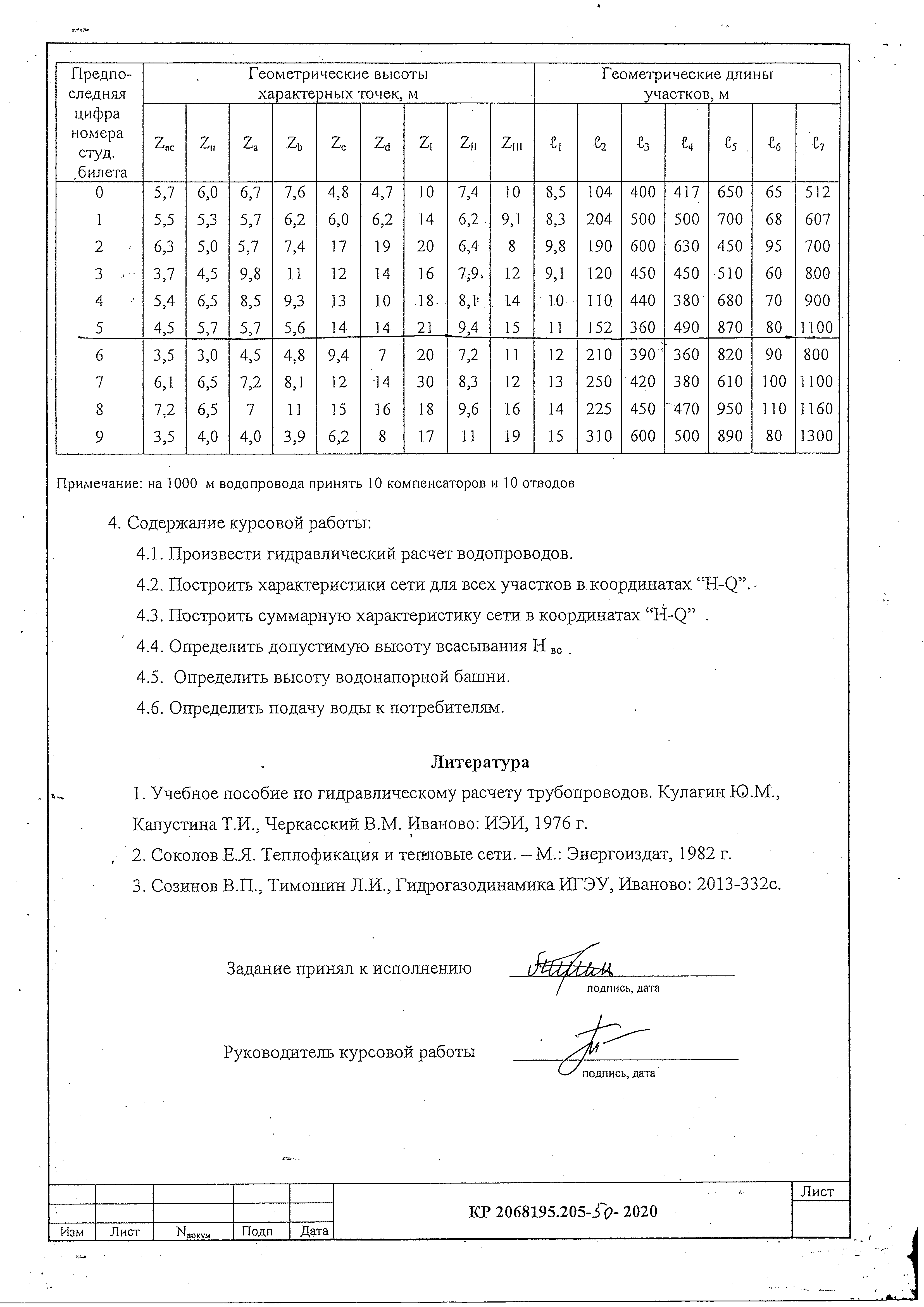Содержание

Введение.

1. 
   Гидравлический расчет участков линии нагнетания.
   
   1. 
      Гидравлический расчет 7 участка
      
   2. 
      Гидравлический расчет теплообменника
      
   3. 
      Гидравлический расчет 6 участка
      
   4. 
      Гидравлический расчет 5 участка
      
   5. 
      Гидравлический расчет 4 участка
      
   6. 
      Гидравлический расчет 3 участка
      
   7. 
      Гидравлический расчет 2 участка
      
2. 
   Гидравлический расчет линии всасывания (1 участок)
   
3. 
   Расчет высоты водонапорной башни
   

Заключение.

Список используемой литературы
Введение
Трубопроводы являются неотъемлемой частью всех систем теплоснабжения и обеспечивают возможность их бесперебойной работы. В более широком смысле трубопроводы - это транспортные магистрали для подачи потребителю различных теплоносителей (жидкостей, газов, продуктов сгорания и т.д.).

Трубопроводы могут иметь самую различную форму и протяжённость. Трубопроводы делятся на простые, разветвлённые и кольцевые.

Главной задачей гидравлического расчёта трубопроводов является определение падения давления ΔР на участках главной магистрали и в ответвлениях и их увязка, построение суммарной характеристики сети для последующего правильного выбора нагнетателя и подача каждому потребителю заданного расхода теплоносителя.

1. 
   Гидравлический расчет участков линии нагнетания.
   

1. 
   Гидравлический расчет 7 участка
   

Целью данного расчёта является определение диаметра, скорости, удельного коэффициента сопротивления и зависимости падения напора на 7 участке от расхода.

Расчётные данные 7 участка приведены в задании.

Для расчёта диаметра использовано уравнение: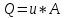

(1.1)

Где А- площадь сечения, м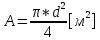².

(1.2)
где d-диаметр, м;

u-скорость потока, м/с.

Скорость движения теплоносителя задается в интервале 0,5-3 м/с. Принимаем u_зад=0,5м/с, на участках 7 и 6 скорость принята минимальной, тогда ориентировочное значение диаметра из формул (1.1) и (1.2):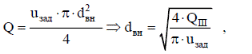



где Q_III=28 л/с=0,028м³/с- расход на 7 участке.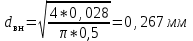


По [1 ] приняты трубы стальные бесшовные горячекатаные с диаметром dн=273 мм и толщиной стенки δ=7мм.

Внутренний диаметр определен по формуле: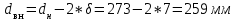

(1.3)

Уточненное значение скорости определено по формулам (1.1) и (1.2):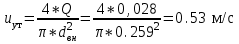



Эквивалентная шероховатость стальных труб [1] (для всех участков сети принята k_э=0,5 мм).

Для определения режима течения определен критерий Рейнольдса по формуле:
(1.4)
где ν-коэффициент кинематической вязкости жидкости [1]
ν_t2= ν₇₈=0,3758 * 10^-6 м2/с: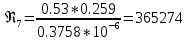

Определено предельное число Рейнольдса по формуле: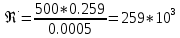
(1.5)


Число Re7 с предельным числом Re, Re7>Re. Следовательно, расчёт коэффициента гидравлического трения необходимо рассчитывать по формуле Шифринсона [1]: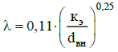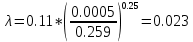




Определено падение напора на 7 участке по формуле Дарси-Вейсбаха:
(1.6)
Для нахождения зависимости потери напора от расхода на 7 участке использована формула: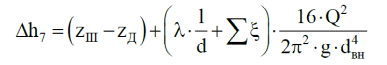
(1.7)
где: ∑ξ- сумма коэффициентов местных сопротивлений по всей длине участка.



где ξотв- коэффициент сопротивления отвода на 90^о, количество отводов n1=11, ξотв=0,5[1],

ξкомп-коэффициент сопротивления компенсатора, при количестве компенсаторов n 2=11; ξкомп=1,7 [2].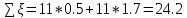



Падение напора на 7 участке по формуле (1.6):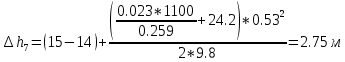



Удельный коэффициент сопротивления В₇ из формулы (1.5) равен: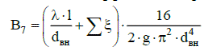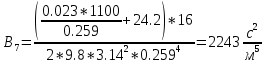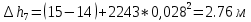








Результаты расчета падения напора по формулам (1.6) и (1.7) равны, следовательно, удельный коэффициент сопротивления В7 рассчитан правильно.

В результате гидравлического расчета 7 участка определены диаметр трубопровода d_вн=0,259м, скорость u=0.53 м/с, падения напора 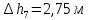и удельный коэффициент сопротивления В₇=2243c²/м⁵ .
1.2 Гидравлический расчет теплообменника
Целью данного расчёта является определение удельного коэффициента сопротивления для теплообменника.

Для теплообменника на участке «c-д» известна потеря напора Δh_т/о. Найден коэффициент удельного сопротивления В_т/о из формулы (1.7):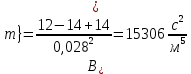


В результате гидравлического расчета т/о участка определен удельный коэффициент со- противления Вт/о=15306 c²/м⁵
1.3 Гидравлический расчет 6 участка
Целью данного расчёта является определение диаметра, скорости, удельного коэффициента сопротивления и зависимости падения давления на 6 участке от расхода.

Так как на 7 и 6 участках расходы равны, следовательно, значения скорости и диаметра трубопровода для 6 участка взяты из гидравлического расчета 7 участка.

Определен критерий Re₆ по формуле (1.4):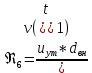


где ν_t1=ν₃₀=0,805*10^-6 м² /с [1] (для дальнейших расчетов участков принято данное значение т.к. температура больше не изменяется)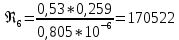



Определено предельное число Рейнольдса по формуле: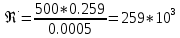


Сравнено число Re₆ с предельным числом Re’, Re₆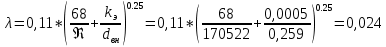
Зависимость падение напора от расхода на 6 участке: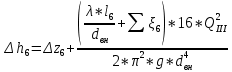

где Δz₆=z_c-z_в=14-5.6=8.4 м.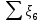
- - коэффициенты местных сопротивлений по длине 6 участка: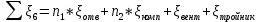

ξ_задв=0,1 [1]- коэффициент местного сопротивления задвижки, задвижка открытая. ξ_отв=0,5;ξ_комп=1,7; количество компенсаторов n₂=1; количество отводов n₁=1 . Значения коэффициента местного сопротивления тройника ξ_{тройник} необходимо принимать для случая разделения потоков, относящихся к части общего расхода, движущегося параллельно направлению скорости суммарного потока. Коэффициент местного сопротивления тройника ξ_{тройник}=3,0 [1], определен по соотношению расходов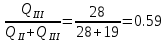

Принят стандартный тройник.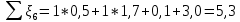


Определены потери напора на 6 участке по формуле (1.6):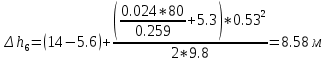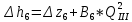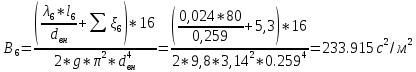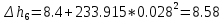






В результате гидравлического расчета 6 участка определены диаметр трубопровода, скорость, падения напора и удельный коэффициент сопротивления В₆

Суммарное падение напора на участках 6 и 7 с учётом теплообменника: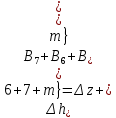



Перепад высот на 7+т/о+ 6 участках Δz=z_III-z_в=15-5.6=9.4 м

В_{(т/о +7+6)}=(15306+2243+233,915)=17782,915 с ² /м⁵
Δh _(т/о+6+7)=9,4+17782,915*0,028²=23,34м.

Для проверки правильности определения удельного коэффициента сопротивления

В_{(т/о +7+6}) определен суммарный перепад напора по формуле:

Δh_(т/о+6+7)= Δh₇+ Δh_т/о+ Δh₆=2,76+12+8,58=23,34м.

Удельный коэффициент сопротивления В_{(т/о +7+6)}определен правильно.

Заданы значения Q_III в интервале 0-0,05м³/с и полученные результаты приведены в

табл.1.1;

Δh(6+7+т/о)=9,4 +17782,915*Q²
Таблица 1.1 Зависимость падения напора от расхода Δh=f(Q) для участков 7+т/о+ 6

Q,м3/с	0	0,007	0,014	0,021	0,028	0,035	0,042	0,049
Δh	9,4	10,27	12,88	17,24	23,34	31,18	40,77	52,10

По данным табл. 1.1 построена зависимость Δh=f(Q) (см. графическое приложение, кривая «h7+т/о+6»).
1.6 Гидравлический расчет 5 участка
Целью данного расчёта является определение диаметра, скорости, удельного коэффициента сопротивления и зависимости падения давления на 5 участке от расхода.

При параллельной работе участков (7+т/о+ 6) и 5 участка необходимым условием является равенство падения напора Δh_(6+7+т/о) и Δh₅. Следовательно Δh₅=23,34 м. Для этого на 5 участке надо увеличить скорость и определить её методом итераций.

Расчётные данные 5 участка представлены в задании . Методом итераций получена скорость на 5 участке u₅=1,31м/с при Q_II =19 л/c=0,019 м3/с.

Согласно формулам (1.1) и (1.2) получили: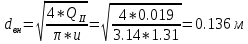

По [1] выбраны трубы стальные бесшовные горячекатаные. Принято dн=146мм, толщина стенки δ=6 мм, тогда по формуле (1.3):

d_вн=d_н – 2* δ=146-6*2=134мм.
Уточнена скорость по (1.1) и (1.2):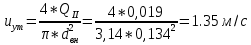



Для определения режима течения определен критерий Рейнольдса по формуле (1.4):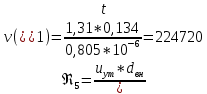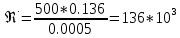


Сравнено число Re₅ с предельным числом Re’, Re₅>Re’. Следовательно, расчёт коэффициента гидравлического трения λ по формуле Шифринсона.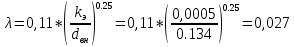


Для определения зависимости потерь напора от расхода использована формула (1.7):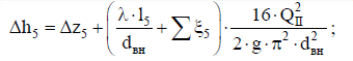



где Δz₅=z_II-z_в=9.4-5.6=3.8 м;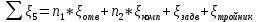

ξ_задв=0,1 [1]- коэффициент местного сопротивления задвижки, задвижка открытая. ξ_отв=0,5;ξ_комп=1,7; количество компенсаторов n₂=15; количество отводов n₁=14 . Значения коэффициента местного сопротивления тройника ξ_{тройник} необходимо принимать для случая разделения потоков, относящихся к части общего расхода, движущегося параллельно направлению скорости суммарного потока. Коэффициент местного сопротивления тройника ξ_{тройник}=1,7 [1], определен по соотношению расход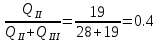ов
и диаметров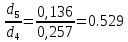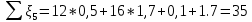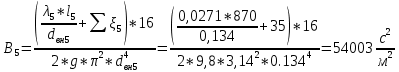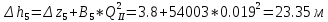






Для проверки правильности определения удельного коэффициента сопротивления

В₅ определен перепад напора на 5 участке по формуле (1.6):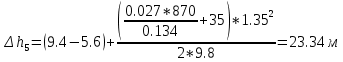

Удельный коэффициент сопротивления В₅ определен правильно

Заданы значения Q в интервале 0-0,03м³/с и полученные результаты приведены в

табл.1.2;
Таблица 1.2 Зависимость Δh=f(Q) для участка 5

Q,м3/с	0	0,005	0,010	0,015	0,019	0,025	0,030
Δh	3,8	5,15	9,2	15,96	23,342	37,58	52,45

По данным таблицы построил график Δh=f(Q) (см. графическое приложение–кривая h₅).

В результате гидравлического расчета 5 участка определены диаметр трубопровода, скорость, падения напора и удельный коэффициент сопротивления В₅.
1.5 Гидравлический расчет 4 участка
Целью данного расчёта является определение диаметра, скорости, удельного коэффициента сопротивления и зависимости падения давления на 4 участке от расхода.

При отрицательном перепаде высот на участке, падение напора не может быть меньше ноля. Так как на 4 участке Δz₄=z_в-z_а=5,6-5,7=-0,1 м, следовательно, скорость определена методом итераций.

Расчётные данные участка представлены в задании. Методом итераций получена скорость u₄=1 м/с.

Q=QIII+ QII

Диаметр трубопровода определяем по формуле согласно (1.2) и (1.1):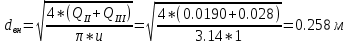


Выбраны трубы стальные бесшовные горячекатаные [1] с d_н=273 мм и δ=10 мм.

Внутренний диаметр трубопровода :

d_вн=d_н-2δ=273-2 ∙ 10=257 мм.

Уточненная скорость движения воды на участке :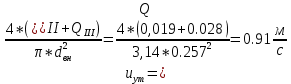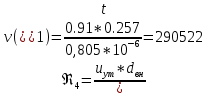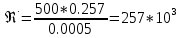




Re₄>Re’, следовательно коэффициент гидравлического трения λ рассчитал по формуле Шифринсона [1].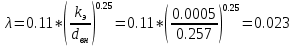

Δz₄=z_в-z_а=5,6-5,7=-0,1 м
Для определения зависимости потерь напора от расхода на 4 участке использована формула (1.7):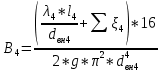

^ξотв ^{и ξ}комп <sup>– найдены аналогично предыдущим участкам.

Значения коэффициента местного сопротивления тройника ξ</sup>тройник ^{необходимо принимать} для случая разделения потоков, относящихся к части общего расхода, движущегося параллельно ^{направлению скорости суммарного потока. Согласно [1] ξ}тройник^{=12, при от}ношении расходов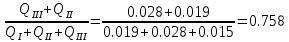

ⁿ1^{=5 и количество компенсаторов n}2<sup>=5.

</sup>45 0,5 5 1, 7 1223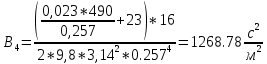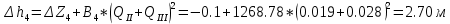



Определены потери напора на 4 участке по формуле (1.6):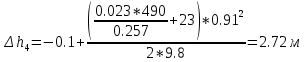

Полученный результат соответствует условию при отрицательном Δz ( Δh ≥ 0 ).
Удельный коэффициент сопротивления В₄ определен правильно.

Таким образом для 4 участка зависимость падения напора от расхода:

Δh4=-0,1+1268,78*Q².

Заданы значения расхода от 0 до 0,055 м3/с и полученные результаты приведены в таблице 1.3.

Таблица 1.3 Зависимость Δh=f(Q) для участка 4.

Q,м3/с	0	0,005	0,01	0,015	0,02	0,025	0,03	0,035	0,04	0,047	0,05	0,055
Δh,м	-0,1	-0,07	0,03	0,18	0,41	0,69	1,04	1,45	1,93	2,70	3,07	3,74

По данным таблицы 1.3 построен график зависимости Δh=f(Q) (см. графическое приложение – кривая h₄).

В результате гидравлического расчета 4 участка определены диаметр трубопровода, скорость, падения напора и удельный коэффициент сопротивления В₄.
1.6 Гидравлический расчет 3 участка
Целью данного расчёта является определение диаметра, скорости, удельного коэффициента сопротивления и зависимости падения давления на 3 участке от расхода.

При параллельной работе суммарных участков (7+т/о+ 6)+4 и 3 участка необходимым условием является равенство падения напоров Δh_(6+7+т/о)+ Δh4 и Δh3.Следовательно Δh3=26,04м. Для этого на 3 участке надо максимально увеличить скорость и для увеличения падения напора до искомой величины установить на 3 участке дроссельную шайбу. Вода, протекая по трубопроводам, движется по пути «наименьшего сопротивления», т.е. большая часть воды пойдет на ответвление, то для обеспечения подачи требуемого количества воды всем потребителям необходимо уравнять потери напора на магистрали и на ответвлении. Для удовлетворения этой цели на трубопроводе ответвления сети установлены дроссельные шайбы . Дроссельная шайба (диафрагма) представляет собой тонкий диск с центральным отверстием круглого сечения. Диафрагма устанавливается (врезается) по оси трубопровода. Вследствие установки диафрагмы поток жидкости испытывает внезапное сжатие, а затем расширение, т.е. диафрагма, по сути, является местным сопротивлением.

Расчётные данные 3 участка представлены в задании. Задана скорость u3=1,2 м/с.
Диаметр определен согласно формулам (1.1) и (1.2):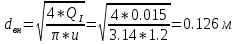


где Q_I=0,015 м³/с.
^{Выбраны трубы стальные бесшовные горячекатаные, принято d}н^{=133 мм, δ=5 мм [1], то-}гда внутренний диаметр трубы равен:
d_вн=d_н-2δ=133-2 ∙ 5=123 мм.
Уточнена скорость по (1.1) и (1.2):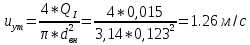



Для определения режима течения определен критерий Рейнольдса по формуле (1.4):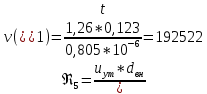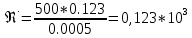


Сравнено число Re₅ с предельным числом Re’, Re₃>Re’. Следовательно, расчёт коэффициента гидравлического трения λ по формуле Шифринсона.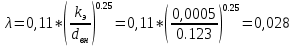


Для определения коэффициента местного сопротивления дроссельной шайбы использована формула (1.6):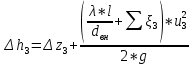

где Δz₃=z₁-z_а=21-5.7=15.3 м; Δh3=26.04м;
_₃ - сумма коэффициентов местных сопротивлений по длине 3 участка;

_^₃ ^n₁ ^_отв ^n₂ ^_комп ^_задв ^+ξтройник +^ξдрос.ш
^ξотв, ^ξкомп^{, ξ}задв <sup>–определены аналогично предыдущим участкам, количество ответвле-

ний n</sup>1^{=4 и количество компенсаторов n}2<sup>=4.

Значения коэффициента сопротивления тройника ξ</sup>тройника ^{необходимо принимать для} случая разделения потоков, относящихся к части общего расхода, движущегося перпендикулярно направлению скорости суммарного потока. Коэффициент местного сопротивления

^{тройника ξ}тройник^{=1.6[1], определен при соотношению расходов}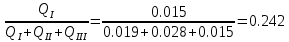

и диаметров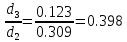

После решения уравнения получен коэффициент местного сопротивления дроссельной шайбы ξ_дрос.ш.=40.1.
₃ 40,5 41, 7 0,11.640.150.6
Тогда для 3 участка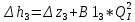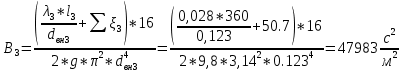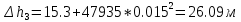




Зависимость падения напора от расхода на 3 участке:

Δh₃=15,3+47983*Q²
Заданы значениями расхода в интервале от 0 до 0,03 м3/с и и полученные результаты приведены в таблице 1.4
Таблица 1.4 Зависимость Δh=f(Q) для участка 3

Q,м3/с	0	0,005	0,010	0,015	0,020	0,025	0,030
Δh	15,3	16,5	20,09	28,08	34,47	45,26	58,44

По данным таблицы построила график Δh=f(Q)( см. графическое приложение-кривая h3)

В результате гидравлического расчета 3 участка определены диаметр трубопровода, скорость, падения напора и удельный коэффициент сопротивления В3.
1.7 Гидравлический расчет 2 участка
Целью данного расчёта является определение диаметра, скорости, удельного коэффициента

сопротивления и зависимости падения давления на 2 участке от расхода.

^{Расчётные данные для 2 участка представлены в задании. Задана скорость: u}2^=0,8м/с.

Внутренний диаметр трубопровода определен согласно формулам (1.1) и (1.2)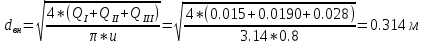


где - Q2= QI+QII+QIII

Выбраны трубы стальные бесшовные горячекатаные с dн=325 мм и толщиной стенок δ=8 мм [1].

Внутренний диаметр по ГОСТ:
d_вн=d_н-2δ=325-2 ∙ 8=309 мм.
Уточненная скорость определена по формуле: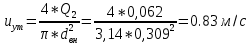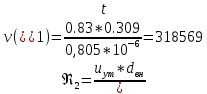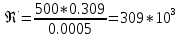



Re₂>Re’, следовательно коэффициент гидравлического трения λ рассчитал по формуле Шифринсона [1].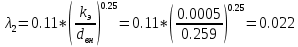

Определена зависимость потери напора от расхода на 2 участке: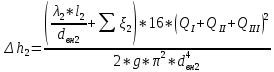

^{где Δz}2^=za^-zн^{=5.7-5.7=0 м;}
_₂ - сумма коэффициентов местных сопротивлений по длине 2 участка .

^2 ^n1 ^отв ^n2 ^комп ^задв ^о.к. <sup>;

ξ</sup>комп^{, ξ}отв^{, ξ}задв – ^{аналогично предыдущим участкам, количество ответвлений n}1^{=2 и количе- ство компенсаторов n}2^=2;

_о.к. - коэффициент местного сопротивления обратного клапана, _о.к. =2,1[1].
₂ 2 0,5 2 1, 7 0,12,1 6, 6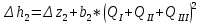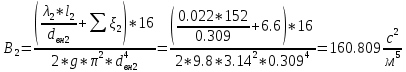


Зависимость падения напора от расхода на 2 участке: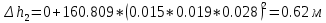


Определены потери напора на 2 участке по формуле (1.6):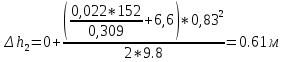

^{Удельный коэффициент сопротивления В} 2 ^{определен правильно.} Таким образом для 2 участка зависимость падения напора от расхода :

^Δh2^=160,809*Q2²

Заданы значениями расхода в интервале от 0 до 0,75м³/с и результаты расчета занесены в таблицу 1.5

Таблица 1.5 Зависимость Δh=f(Q) для участка 2.
По данным таблицы 1.5 построена зависимость Δh=f(Q) (см. графическое приложение – ^{кривая h}2^).

В результате гидравлического расчета 2 участка определены диаметр трубопровода, скорость^{, падения напора и удельный коэффициент сопротивления В}2^.

Q,м3/с	0	0,01	0,02	0,03	0,04	0,05	0,062	0,07	0,08
Δh	0	0,016	0,064	0,145	0,257	0,402	0,618	0,788	1,029

2.Гидравлический расчёт линии всасывания
Целью данного расчёта является определение допустимой высоты всасывания.

Расчётные данные 1 участка приведены в задании. Скоростью на линии всасывания изменяется в интервале 0,3-0,5 м/с с целью минимизации потерь напора. Задана u1=0,3 м/с.

Согласно формулам (1.1) и (1.2) рассчитан внутренний диаметр: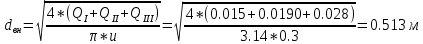


^{Приняты [1] трубы чугунные водопроводные с d}н^{=532 мм и толщиной стенок δ=15,6 мм.}

Внутренний диаметр трубопровода определен по формуле:

d_вн 532 2  500,8 мм.
Уточненная скорость определена по формуле: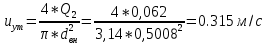

Для определения режима течения определен критерий Рейнольдса по формуле (1.4):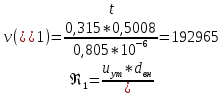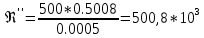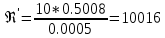



Re’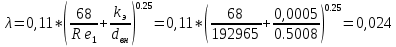

Составлено уравнение Бернулли для 1 участка с учётом потерь: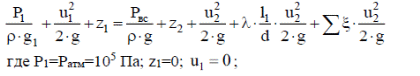


^Рвс^{=1,1 Р}нас<sup>(давление на линии должно быть больше давления насыщения перекачиваемой

воды, при этом условии не возникает явление кавитации)</sup> ^{следовательно при t=30о и Р}нас^{=0,04241105 Па [1],P}вс<sup>=0,0466105Па;

Скорость на линии всасывания u</sup>2^=uвс^{=0,315 м/с; плотность воды ρ(t}1^{)=995.6 кг/м3[1];}

_- сумма местных сопротивлений:

_= _отв _задв _вк =0,5+0,1+2,5=3.1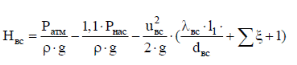

^
_вк^{- коэффициент местного сопротивления всасывающего клапана; ξ}вк^=2,5[1].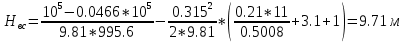


Определена допустимая высота всасывания, которая составила 9,71м.

Перепад высот на линии всасывания z_вс=3,5 м

Перекачка воды при условии H_вс>z_вс не приведет к возникновению кавитации в насосе .
3.Расчет высоты водонапорной башни
Целью данного расчёта является определение высоты водонапорной башни.

Водонапорная башня начинает работать при отключении насоса и подает воду ко второму

и третьему потребителям. Q_в.б=Q_III+ Q_II Задана скорость u=0,1 м/с.

Определен внутренний диаметр согласно (1.2) и (1.1):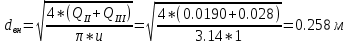


Выбраны трубы стальные бесшовные горячекатаные [1] с d_н=273 мм и δ=10 мм.

Внутренний диаметр трубопровода :

d_вн=d_н-2δ=273-2 ∙ 10=257 мм.

Уточненная скорость движения воды на участке :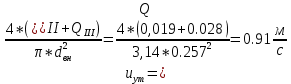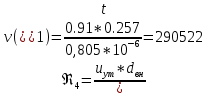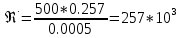




Re₄>Re’, следовательно коэффициент гидравлического трения λ рассчитал по формуле Шифринсона [1].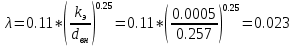


Сумма местных сопротивлений в опускной трубе водонапорной башни:

^{}пов ^задв ^вх.в.трубу

-коэффициент местного сопротивления вход в трубу;



Записано уравнение Бернулли для водонапорной башни: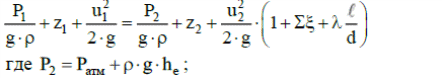



Напор в тосчке «е» h_e=^Δh4 ^{/2 + Δh}5=2.72/2+23.34=24.7м
длина опускной трубы z₁ 2 ; при высоте бака водонапорной башни 2м;

^z₁ ^z_в.б^{; z}2^{=0; u}1^{=0 ; u}2 ^=uут
Из уравнения Бернулли, выражено^zв.б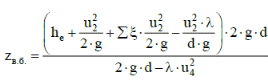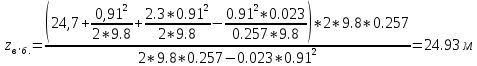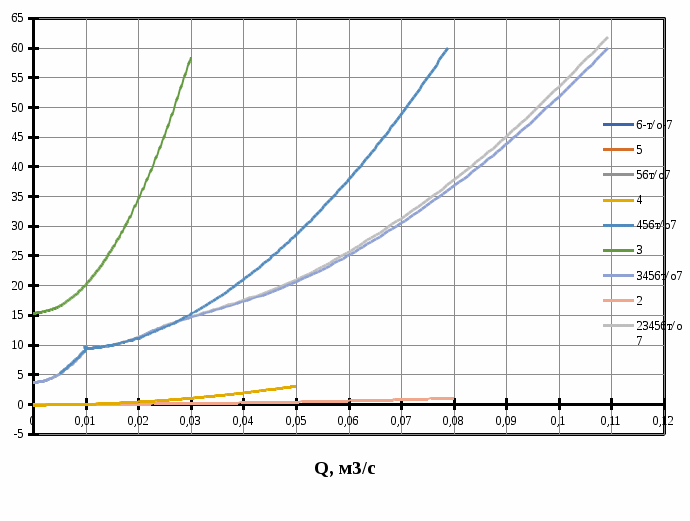



Заключение
По полученным данным для зависимости падения напора от расхода построены характеристики сети для всех участков и суммарные характеристики сети в координатах Δh-Q.

Из графика были получены напор на линии нагнетания hнаг =26,7 , напор в узловых точках «а» hа =26,6 и «в» h2= ,падение напора на всех участках Δh2=0,61 , Δh3=26,09 , Δh4=2,7 , Δh5=…34,24., Δh7+т/о+6=253,24 .Полученные результаты полностью совпали с расчетными.

Расход к первому потребителю Q1=0,015 определен пересечением прямой hа с графиком h3,

Расход ко второму потребителю Q2 =0,019 определен пересечением прямой hb с графиком h5, расход к третьему потребителю Q3 =0,028 определен пересечением прямой hb с графиком h6+т/о+7.Полученные данные совпадают с заданием, следовательно расчет произведен правильно.

В ходе гидравлического расчета водопровода состоящего из 7 расчетных участков и подогревателя ,на каждом участке определена скорость и ГОСТ диаметр трубы. Определены режим течения и коэффициент гидравлического трения на всех участках. Выбраны коэффициенты местных сопротивлений на участках и рассчитана их сумма. Рассчитаны потери напора для каждого участка водопровода и получена зависимость падения напора при различных расходах .Построены графики зависимости падения напора от расхода для Δh6,7,т/о; Δh5; Δh4; Δh3 и Δh2 участков .. Рассчитана высота водонапорной башни z=24.93 . Определена допустимая высота всасывания .H=9.71.

Список используемой литературы:
1. Кулагин, Юрий Михайлович. Учебное пособие по гидравлическому расчету тру- бопроводов / Ю. М. Кулагин, Т. И. Капустина, В. М. Черкасский ; Ивановский энергетический институт имени В. И. Ленина.—Иваново: Б.и., 1976.—70 с.

2. Соколов, Ефим Яковлевич. Теплофикация и тепловые сети: [учебник для вузов] / Е. Я. Соколов ; под ред. В. А. Малафеева.—7-е изд., стер..—М.: Изд-во МЭИ, 2001.—472 с.