Курсовая. КУРСОВАЯ РАБОТА ЕПТЬ (1). Гидравлика и нефтегазовая гидромеханика
 Скачать 148.13 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования (УГНТУ) «Уфимский государственный нефтяной технический университет» Факультет трубопроводного транспорта (ФТТ) Кафедра гидрогазодинамики трубопроводных систем и гидромашин (ГТ) Курсовая работа: «Гидравлический расчет сложного трубопровода и элементов оборудования» по дисциплине «Гидравлика и нефтегазовая гидромеханика» Выполнил: студент гр. БГР-20-01 Проверил: доцент, к.т.н. А.У. Мухаметов Н.В. Морозова Уфа 2022 СОДЕРЖАНИЕ 1. Решение задач………………………….…….…...…………………………… 1.1 Задача 4…………………….…………………………………………………. 1.2 Задача 7...…………………...………………………………………………… 2. Гидравлический расчет разветвленного трубопровода………………..... 3. Вывод……………………………………………...………………………….. Список использованных источников ……………………………………….. ЗАДАНИЕ на выполнение курсовой работы по дисциплине «Гидравлика и нефтегазовая гидромеханика»
Тема работы «Гидравлическийрасчеттрубопроводовиэлементов оборудования». Исходные данные приведенывтаблице:
РаинкинаЛ.Н.Гидромеханика.Учебноепособиепорешениюзадач-М.:РГУнефтиигазаим.И.М. Губкина, 2005. -131 с. Разбегина Е.Г., Сумбатова А.Р. Прикладные задачи гидравлики. Учебное пособие по дис-циплинам«Гидравлика»и«Гидромеханика».-М.:РГУнефтиигазаим.И.М.Губкина,2007.-86с. Решение задач: Задача 4 (раздел 4). Сборник задач [1]. Определить суммарную силу давления на торцевую стенку АВ горизонтальной цилиндрической цистерны диаметром d, заполненной жидкостью плотностью ρ, если уровень жидкости в горловине находится на расстоянии H от дна. Цистерна герметически закрыта и над поверхностью жидкости находится газ. Давление газа может быть больше атмосферного (тогда показание мановакууммера равно рм0) или меньше атмосферного (тогда показание мановакуумметра равно рv0). Определить также координаты точки приложения силы давления. 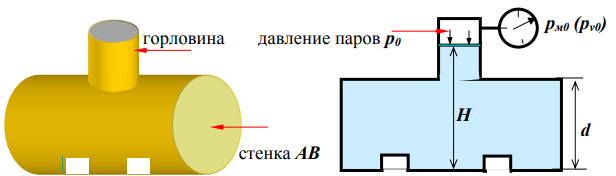 Рисунок 1 - к задаче 4 Указания 1. Плотность жидкости определите с помощью Приложения 1, а момент инерции круга - по Приложению 2. 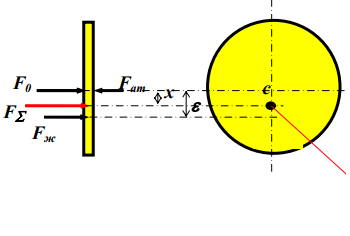 2. Схема сил, действующих на стенку АВ:F0 - сила внешнего давления; Fж - сила весового давления; Fат – сила атмосферного давления; FΣ - суммарная (равнодействую-щая) сила давления на стенку цистерны. Точка приложения силы давления FΣ (величина х определяется по теореме Вариньона) Таблица исходных данных
Решение: Поскольку над поверхностью жидкости имеет место вакууметрическое давление р, создаваемое силой Fо, действующей на стенку, то в таком случае: S – смоченная площадь стенки. 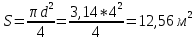 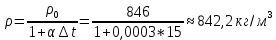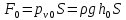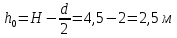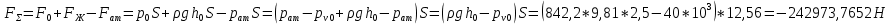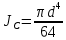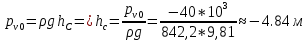;Плотность диз.топлива определим по формуле:  - плотность при t=35°;Сила вакууметрического давления определяется по формуле:  , где h – глубина погружения центра тяжести от свободной поверхности жидкости; При давлении на поверхности жидкости меньше, чем атмосферное:   – момент инерции фигуры для нашего случая; – пьезометрическая высота;Координата точки приложения силы относительно центра тяжести стенки теореме Вариньона: 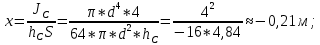 Относительно свободной поверхности: 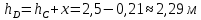 .Ответ: FΣ= -242973,7652; х=-0,21 м. Задача 7 (раздел 6). Сборник задач [1]. Для поддержания пластового давления при добыче нефти в нагнетательную скважину глубиной H по насосно-компрессорным трубам (диаметр d, длина l, шероховатость Δэ) закачивается Q м3 воды в сутки. Забойное избыточное давление равно рзаб. Температура воды t°C. Показание устьевого манометра рм. Определить диаметр трубопровода. 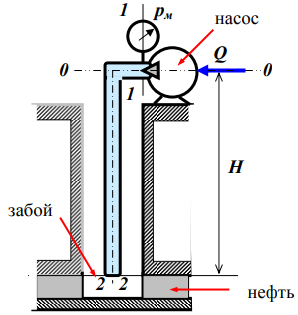 Рисунок 2 - к задаче 7 Таблица исходных данных Указания Примените уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0. При расчете потерь учтите только потери по длине. Местными потерями пренебречь. Принять длину трубопровода равной H. Задачу решить методом итераций, предполагая турбулентный режим движения.
Решение: Аргумент равен функции от аргумента - Q =φ(Q). 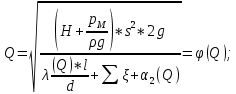 Задаёмся некоторым начальным значением λ0коэффициента трения и значением коэффициента Кориолиса α0. Примем для турбулентного режима: 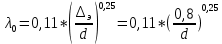 α0 =1 Определяется правая часть уравнения - функция φ(Q), то есть начальное значение расхода жидкости Qo. 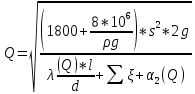 Задача № 17. Сборник задач [2]. Рассчитать промысловую систему, указанную на схеме, состоящую из трех разводящий линий L1, d1, L2, d2, L3, d3, нагнетательной линии насоса L0, d0. В конечных пунктах заданы давления, р1, р2, р3и уровни жидкости в резервуарах z1, z2, z3. Даны физические свойства жидкости ν, ρ. Дано давление на выходе из насоса р0. Все трубы стальные бесшовные новые, расположены в одной горизонтальной плоскости. Определить расходы в ветвях и расход в нагнетательной линии насоса, а также давление в узловой точке А. 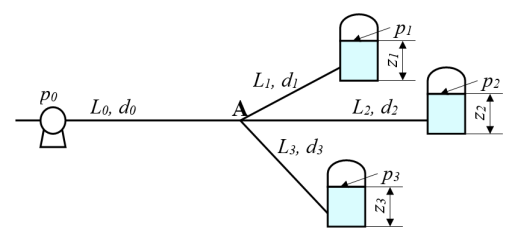 Исходные данные:
Δэ=0,035 мм Решение: Обозначим сечения: 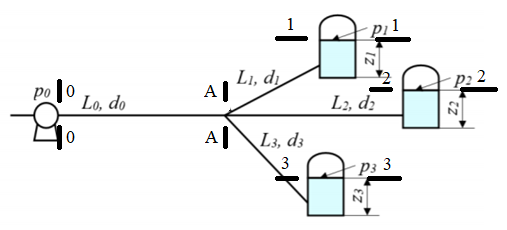 Для выбранных сечений запишем уравнение Бернулли: 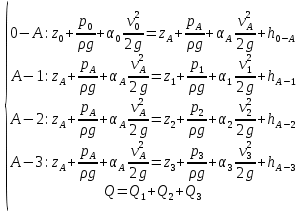 Допустим, что трубопровод 0-А находится в одной горизонтальной плоскости (z0=zA); так как простые трубопроводы имеет постоянный диаметр, скоростные напоры в начальном и конечном сечениях равны: 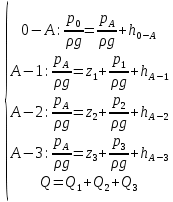 Сделаем замену: 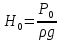 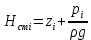 – статические напоры в соответствующих сечениях.Далее преобразуем: 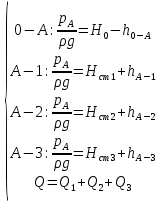 (1)Решим систему (1) графо-аналитически: 3.1) Построим характеристики каждого участка: 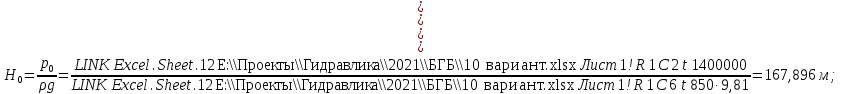 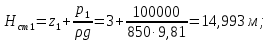 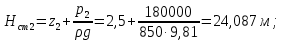 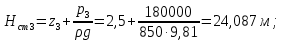 Трубопровод 0: Найдем потери на трубопроводе при различных скоростях для построения характеристики трубопровода 0-А. Принимаем расход жидкости по трубопроводу равной Q0 = 20 м/с. Диаметр известен. 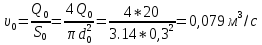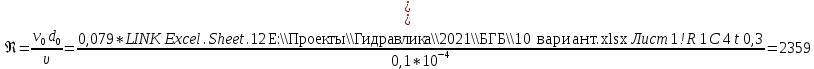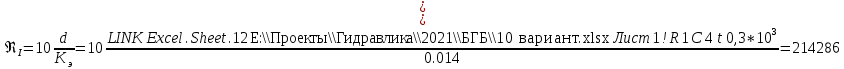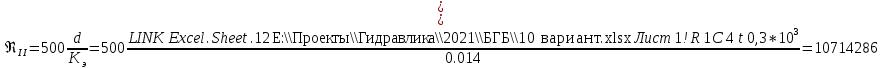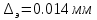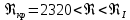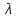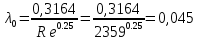Скорость движения жидкости в трубопроводе 0-А будет равна:  Рассчитываем число Рейнольдса:  Рассчитываем переходные числа Рейнольдса:  ,   – для новых стальных бесшовных трубПолученное число Рейнольдса  из чего следует, что в первом трубопроводе турбулентный режим течения (зона гладкого трения).Коэффициент гидравлического сопротивления  определяем по формуле Блазиуса: Рассчитываем суммарные потери напора в трубопроводе 0 без учёта местных потерь: 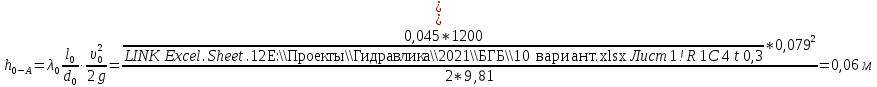 ; 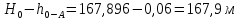.Аналогичные вычисления выполняются для других скоростей. Таблица 1 – Данные для построения гидравлической характеристики участка № 0
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||