Задание_к_РГР-1_и_РГР-2_ (3). Гидродинамика одномерных напорных течений и гидравлические сопротивления
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
Задание на расчетно-графическую работу часть 1(РГР-1) и часть 2 (РГР-2) по темам ГИДРОДИНАМИКА ОДНОМЕРНЫХ НАПОРНЫХ ТЕЧЕНИЙ И ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ Целью настоящей работы является овладение методикой определения гидродинамических характеристик одномерного потока несжимаемой жидкости, включая расчет потерь гидродинамического напора на местных сопротивлениях и сопротивлениях по длине. 1 Введение Закономерности одномерных напорных течений несжимаемой жидкости приводятся в Л5, Л6 и Л7 лекционного курса. Расчётно-графическая работа (РГР) состоит из двух взаимосвязанных частей. В РГР часть 1 (РГР-1) выполняется расчёт гидросистемы, как простого трубопровода с учетом потерь гидродинамического напора на местных сопротивлениях и сопротивлениях по длине. В РГР часть 2 (РГР-2) выполняется расчёт модернизированной гидросистемы и определяется её эффективность с учётом данных по результатам РГР-1. Основные положения методики расчета простых трубопроводов приводятся в п. 7.2.1, Л7. Отчетные материалы частей 1 и 2 настоящей РГР оформляется в соответствии с требованиями по разделу 2 задания, где основные положения отмечены зеленым цветом, желтым цветом отмечены требования, на которые следует обратить особое внимание. Красным шрифтом отмечены, впервые встречающиеся по данному тексту, термины и понятия. 2 Основные требования к отчетному материалу 1. Отчетный материал как для РГР-1, так и для РГР-2 должен содержать титульный лист, условия задачи, решение задачи, ответ по решению задачи. При расположении РГР-1 и РГР-2 в одном файле допускается единый титульный лист. 2. На титульном листе указываются название работы и части РГР, индивидуальный номер варианта задания, фамилия и инициалы автора, группа ИДДО. Форма титульного листа может быть скопирована из раздела 3 данного задания. 3. Условия задачи с исходной гидравлической схемой копируются из раздела 4 задания для указанного индивидуального варианта (по первой цифре его номера) с подстановкой численных значений по второй цифре номера варианта. К полнотекстовым условиям добавляется краткая запись числовых данных и функциональных зависимостей, присутствующих в текстовом поле. Отдельно указывается величина, определяемая в результате решения. При расположении РГР-1 и РГР-2 в одном файле допускается единое полнотекстовое условие. Но краткая запись числовых данных для каждой части РГР должна быть своя. Причём, в условиях РГР-2 данные из решения по РГР-1 отображаются, возможно, с другим обозначением, но с указанием на это решение, полным наименованием и обязательной привязкой к расчётной гидравлической схеме для РГР-2. 4. На расчётной гидравлической схеме должны быть показаны контрольные сечения для используемого уравнения Бернулли. Их неправильное назначение, а также отсутствие на схеме является наиболее серьезной ошибкой расчета. 5. Каждый элемент решения должен начинаться с записи отдельной строкой исходного расчётного уравнения или формулы, под которыми понимаются уравнения и формулы хорошо известные в научной и учебной литературе и вывод которых дан в настоящем лекционном курсе. Как правило, эти уравнения и формулы имеют собственные названия, которые следует приводить перед их написанием. Исходные уравнения и формулы приводятся в том виде, в котором они фигурируют в лекционном курсе (вид уравнений и формул определяется не обозначениями и тем более не индексами, а их структурой, то есть перечнем, расположением и наименованиями используемых параметров). 6. Для каждого обозначения должно быть указано наименование соответствующего параметра непосредственно за уравнением или формулой, где обозначение впервые встречается. Обозначения, за исключением индексов, должны соответствовать лекционному курсу. В дальнейшем решении указанные обозначения, включая обозначения в условиях задачи, не должны меняться. Наименования используемых параметров должны быть точными и полными — они, как правило, являются терминами с определениями, приводимыми в лекционном курсе. Например, в ниже следующем примере v2 не скорость, а средняя скорость на выходе диффузора. «Средняя скорость» — термин, а индекс «2» относит эту скорость к выходу диффузора. Если параметр фигурирует в разных местах проточного тракта и может отличаться по своим значениям, то используются разные индексы при соответствующем основном обозначении, например, v1, v2 и т. д. Обозначения в условиях задачи имеют приоритет перед другими возможными обозначениями. Причем, дополнительные обозначения одной и той же величины не вводятся. 7. Все параметры в контрольных сечениях обозначаются с индексами, соответствующими обозначениям (номерам) этих сечений. При этом в тексте и на гидравлической схеме дополнительных указаний о местоположении этих параметров можно не делать. В остальных случаях местоположения гидродинамических параметров (скорости и давления) указываются на расчётной гидравлической схеме в обязательном порядке. Все параметры в трубопроводе условно относятся к его оси. 8. Для нивелирных высот, входящих в уравнение Бернулли, на расчётной гидравлической схеме должна быть указана плоскость сравнения и ось координаты z (исходную гидравлическую схему, как отдельный рисунок, показывать не следует). 9. В исходных формулах и уравнениях следует использовать избыточное давление. В случае наличия вакуумметрического давления оно учитывается как избыточное со знаком «минус». Коэффициент кинетической энергии принимается равным единице. Скорость течения в резервуаре на достаточном удалении от входа в трубопровод полагается равной нулю. 10. Уравнения, формулы и обозначения, включая обозначения на гидравлической схеме, разрешается выполнять в рукописном виде. Индексы и степени должны изображаться в классическом виде, знак умножения, как правило, не ставится. Примечание: При нанесении дополнительного рисунка на исходный рисунок в приложении «Word» эти рисунки при передаче данных могут смещаться, поэтому рекомендуется делать единый рисунок путем, например, использования вырезки экрана, либо путем перевода всего материала в формат «PDF». При затруднении в оформлении материала в электронном виде разрешается его оформление в рукописном виде с последующим сканированием, при этом текст и формулы должно быть достаточно четкими. 3 Пример расчета гидродинамических характеристик одномерного потока жидкости Различные особенности метода расчета одномерных течений несжимаемой жидкости и соответствующие примеры можно видеть в главах 7 и 9 сборника задач [1]. Ниже рассматривается пример такой задачи по расчету простого трубопровода с наличием энергетического объекта в виде гидравлической турбины. Цифровые данные в этом примере заменены многоточиями. В отчетном материале цифровые данные должны приводиться вместе с размерностью, причем, размерность выставляется только в правой части равенства, например, средняя скорость течения равна: 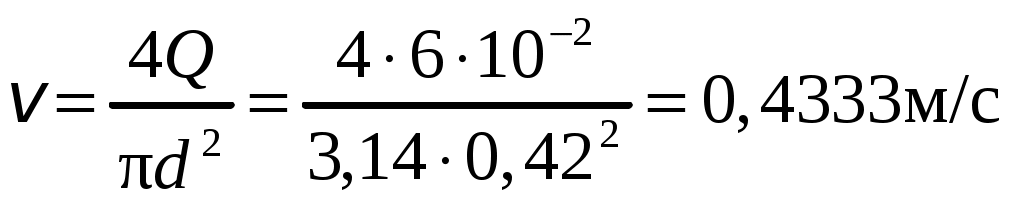 . (1) . (1)Причем, цифровые данные рекомендуется подставлять в системе СИ, а арифметическое равенство должно быть точным, при этом в соответствии с точностью обычных гидравлических расчетов в промежуточных результатах учитываются четыре значащих разряда, а в окончательном результате (ответе) — три значащих разряда. Если размерность указанных исходных данных не в системе СИ, то соответствующий перевод данных делается заранее (до подстановки в уравнение), например, в перечне под грифом «Дано» (см. ниже) можно записать: Q1 = 30 м3/ч = 0,833·10–2 м3/c. В приводимом примере пояснения и рекомендации за пределами решения записаны курсивом. Названия исходных расчетных формул и уравнений выделены синим цветом Национальный исследовательский университет "МЭИ"  Институт дистанционного и дополнительного образования ——————————————————————————————- РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА по курсу: «Гидромеханика» часть первая (либо «части первая и вторая») ГИДРОДИНАМИКА ОДНОМЕРНЫХ НАПОРНЫХ ТЕЧЕНИЙ И ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ Вариант расчетного задания …
Условия задачи: Определить напор на турбине Hт (так называемый «напор нетто») при заданных геометрическом напоре H = …, расходе Q = …, избыточном давлении p0 = … в верхнем баке и вакуумметрическом давлении pв = … в нижнем баке. Заданы также диаметр трубопровода d1 = … до и после турбины, его суммарная длина L = …, эквивалентная шероховатость Δэ = … и коэффициент кинематической вязкости жидкости (ν = …), коэффициенты сопротивления на задвижке (ζз = …), диафрагме (ζд = …), колене (ζк = …), коэффициент полноты удара диффузора (φ = …) и диаметр на его выходе (d2 = …). 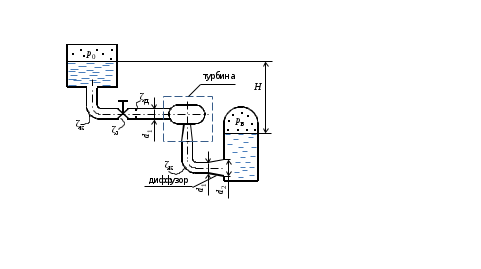 _______________________________________________________________ _______________________________________________________________Примечания: а) условия задачи включаются в отчетный материал в заданном виде вместе с исходной гидравлической схемой, которая дополняется графическими указателями (контрольными сечениями и т. п.) до расчётной гидравлической схемы; б) иногда, графические указатели для некоторых параметров, приводимых в условиях задачи, не указаны на исходной гидравлической схеме, в этом случае такие указатели с соответствующими обозначениями должны быть проставлены на данной схеме самостоятельно в начале решения задачи; в) дополнительно условия задачи приводятся в виде перечня числовых данных так, как указано ниже. Дано: H = …, Q = …, p0 = …, pв = …, d1 = …, L = …, Δэ = …, ν = …, ζз = …, ζд, = …, ζк = …, φ = …,d2 = …. ___________________________________________ Определить: Hт.=? ————————————- Решение задачи 1. Анализ условий задачи в соответствии с первым пунктом методики расчета (п. 7.2.1, Л7). Устанавливаются присутствующие гидравлические сопротивления и потери: кроме сопротивления по длине L трубопровода и местных сопротивлений, указанных в условиях, в схеме присутствуют потери на входе в трубопровод и на выходе из него. Для коэффициента сопротивления на входе в соответствии с геометрией входа следует принять ζвх = 0,5 (см. подпункт 6.4.3.4 Л6). Отметим, что для других конфигураций входа величина ζвх может быть другой. Для коэффициента сопротивления на выходе в резервуар, считая течение турбулентным (турбины не работают на ламинарных режимах течения), примем приближенное значение ζвых = 1 (см. подпункт 6.4.3.2 Л6). Отметим, что в случае, если контрольное сечение находится в трубопроводе или на его выходе, что часто бывает при истечении в атмосферу из проточного тракта, то потери на выходе отсутствуют (примером решения задачи при таком условии может служить вывод формулы для истечения из отверстий и насадков по п. 7.1, Л7 ). Диффузор за турбиной, указанный на схеме, является элементом турбоагрегата и потери в нем входят в искомый напор на турбине. Коэффициенты остальных местных сопротивлений указаны в условиях задачи (на практике эти коэффициенты определяются по справочникам гидравлических сопротивлений, или экспериментальным путем). Отметим, что в предлагаемых задачах могут быть и другие местные сопротивления, которые не указаны в условиях и которые требуется определить самостоятельно по гидравлиической схеме тракта протекания жидкости в соответствии с перечислением сопротивлений по п. 6.4.3, Л6. Для всех участков цилиндрического трубопровода по условию присутствует один диаметр d1 и одна величина эквивалентной шероховатости. Расход и, следовательно, скорость, число Рейнольдса, коэффициент гидравлического трения на этих участках одинаковы. Поэтому потери по длине должны учитываться для суммарной длины (L) этих участков одной формулой Дарси-Вейсбаха. Отметим, что если участки цилиндрического трубопровода имеют различный диаметр, то и потери по длине рассчитываются отдельно для каждого участка. В условиях присутствуют два различных диаметра — d1 и d2. Следовательно, в решении будут присутствовать две различные средние скорости, для обозначения которых целесообразно назначить те же индексы: скорость в цилиндрическом трубопроводе — v1, скорость на выходе диффузора — v2. В соответствии с требованиями к оформлению расчетно-графической работы данные значения наносятся на заданную гидравлическую схему — см. нижеследующий рисунок. 2. Выбор контрольных сечений. Контрольные сечения для уравнения Бернулли являются живыми сечениями и должны проводиться ортогонально линиям тока. Поэтому для наглядности по всей длине течения можно провести линию тока так, как показано на нижеследующем рисунке (не обязательный элемент при оформлении решения). Условие гидростатического распределения давления по сечению, необходимое для назначения контрольных сечений, соблюдается прежде всего в баках с водой. Причем, для напорного бака оно соблюдается на достаточном удалении от входа в трубопровод. Поэтому линию тока следует провести до свободной поверхности воды в баке ортогонально этой поверхности, даже, если реальные линии тока связаны с другим трубопроводом, подсоединенным к баку. Контрольные сечения, как отмечается в п. 7.2.1, Л7, проводятся преимущественно на границах потока, где заданы определенные граничные условия. В рассматриваемой гидравлической схеме этим условиям удовлетворяют сечения, совпадающие со свободными поверхностями жидкости в баках. Их отметка показана на ниже следующем рисунке. Отметим, что в случае отсутствия резервуара на выходе из проточного тракта (истечение в атмосферу) контрольное сечение 2 следует располагать на этом выходе. Обозначать сечения в общем случае можно различными цифрами и буквами, но верхнее, то есть первое по течению, сечение всегда относится к левой части уравнения Бернулли и его принято обозначать цифрой 1. Следующее по ходу течения сечение (нижнее сечение) относится к правой части уравнения Бернулли и его принято обозначать цифрой 2. Все параметры в сечении обозначаются с индексом обозначения этого сечения. Причем, если жидкость движется вверх, то верхним называется сечение внизу пространства. Ввиду того, что индексы 1 и 2 в данной задаче предполагается использовать для трубопровода и на выходе из диффузора, контрольные сечения на гидравлической схеме обозначены индексами 1′ и 2′ со штрихом. 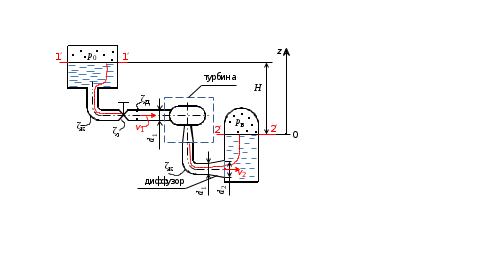 3. На рисунок наносится ось координаты z и плоскость сравнения (нулевое значение z). 4. В случае наличия насоса его напор добавляется в левую часть уравнения Бернулли, напор на турбине, наоборот, вычитается (см. п. 7.2, Л7). Избыточное давление в сечении 1′ (на свободной поверхности) является давлением газа в емкости и обозначено в условиях как p0 (обозначения в условиях задачи имеют приоритет перед другими возможными обозначениями). Коэффициент кинетической энергии принимается равным единице. Уравнение Бернулли для сечений 1′ и 2′: 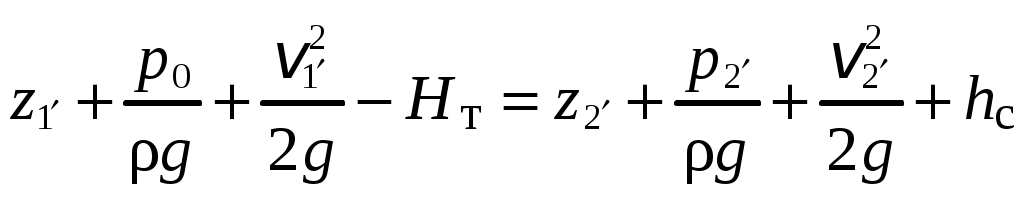 (1) (1)где z1′ = H, z2′ = 0 — нивелирные высоты; v1′ = v2′ = 0 — средние скорости (скорость течения на свободной поверхности в резервуаре принимается равной нулю); p2′ = –pв — избыточное давление (избыточное давление в сечении 2′, которое совпадает со свободной поверхностью жидкости в резервуаре, определяется, заданным по условиям задачи, вакуумметрическим давлением в этом резервуаре); hс — суммарные потери гидродинамического напора. С учетом указанных значений уравнение Бернулли примет следующий вид: 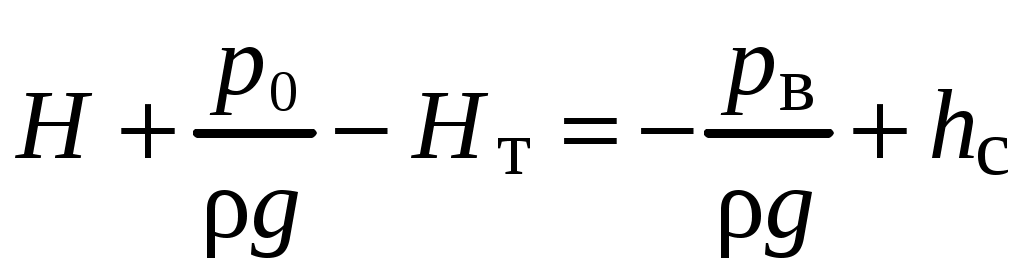 . (2) . (2)5. Суммарные потери напора. Для суммарных потерь гидродинамического напора, справедливо: где 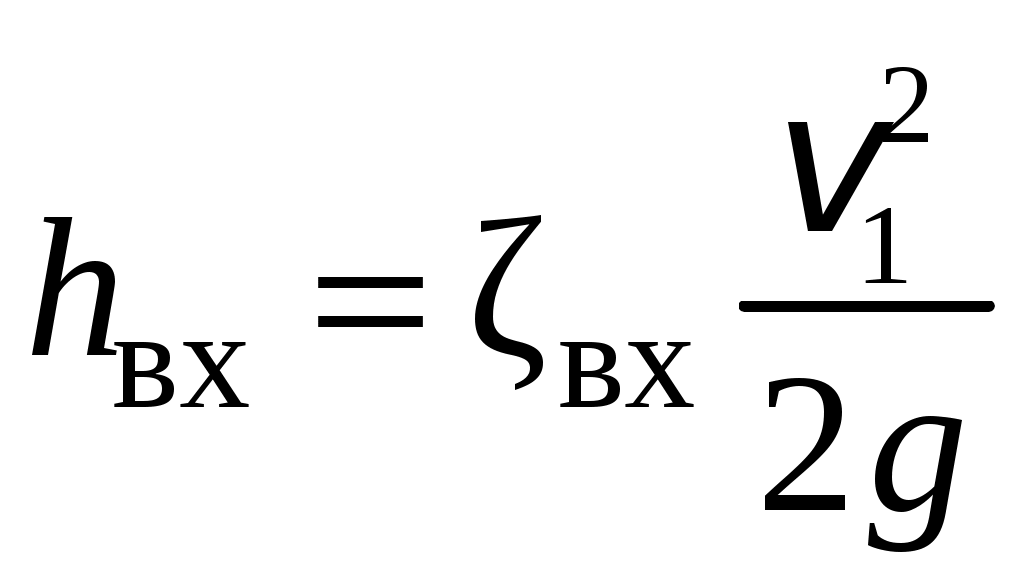 — потери на входе в трубопровод, определяемые по формуле Вейсбаха, в которой v1 — средняя скорость в трубопроводе (показана на рисунке), ζвх = 0,5 — коэффициент сопротивления для входа заданной конфигурации; — потери на входе в трубопровод, определяемые по формуле Вейсбаха, в которой v1 — средняя скорость в трубопроводе (показана на рисунке), ζвх = 0,5 — коэффициент сопротивления для входа заданной конфигурации;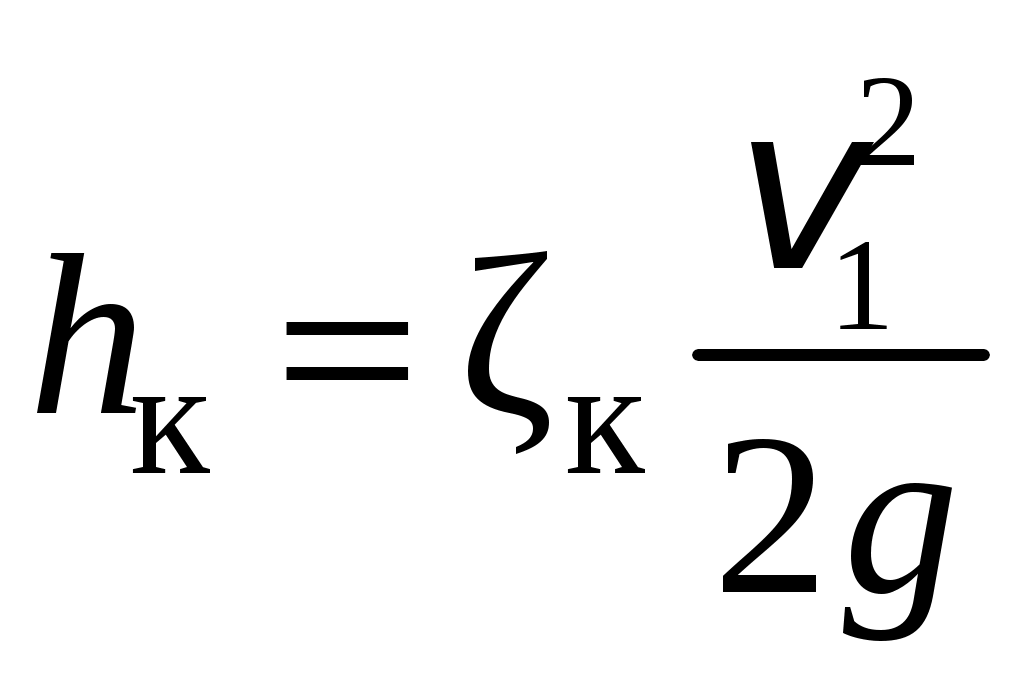 , , 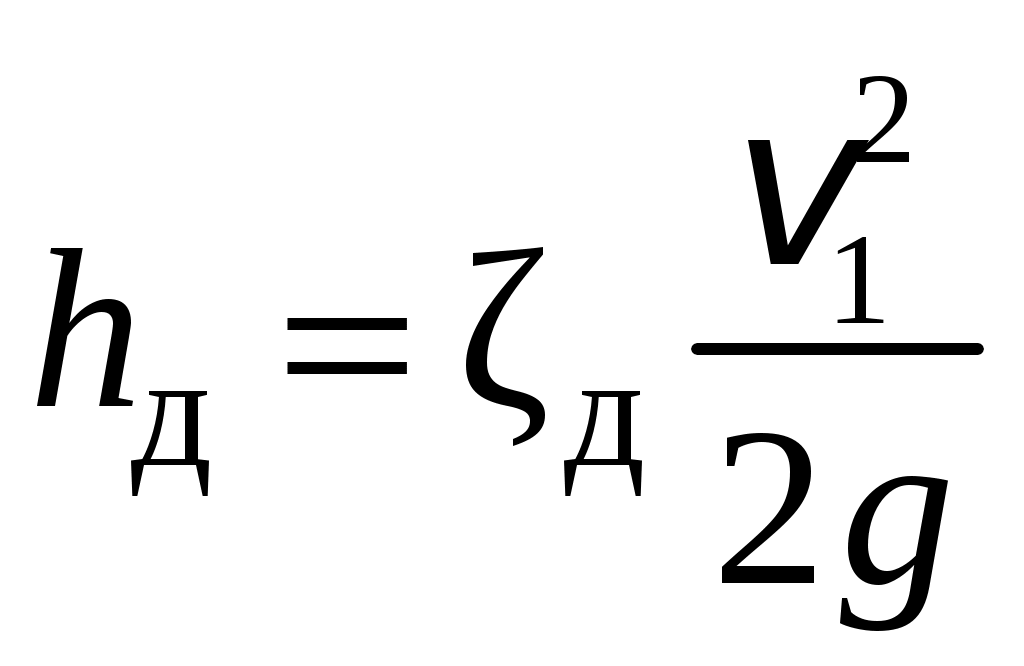 , , 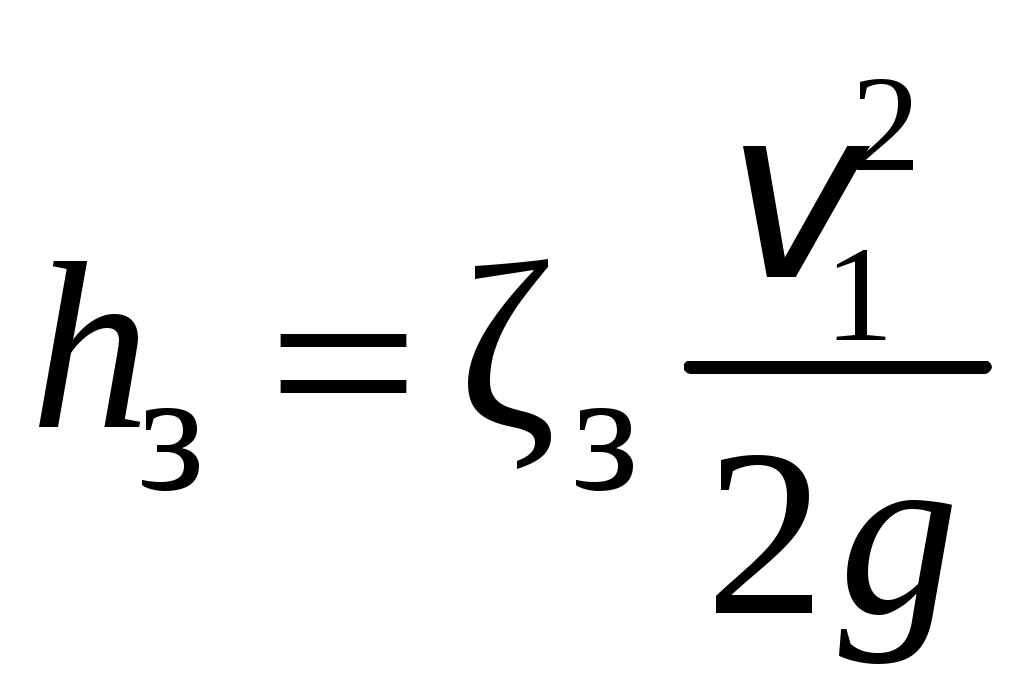 — потери в колене, на диафрагме и на задвижке, соответственно, определяемые по формуле Вейсбаха (проточный тракт имеет 2 колена, поэтому в сумме присутствует 2hк; коэффициенты ζ указаны в условиях задачи; обозначение v1 названо выше); — потери в колене, на диафрагме и на задвижке, соответственно, определяемые по формуле Вейсбаха (проточный тракт имеет 2 колена, поэтому в сумме присутствует 2hк; коэффициенты ζ указаны в условиях задачи; обозначение v1 названо выше);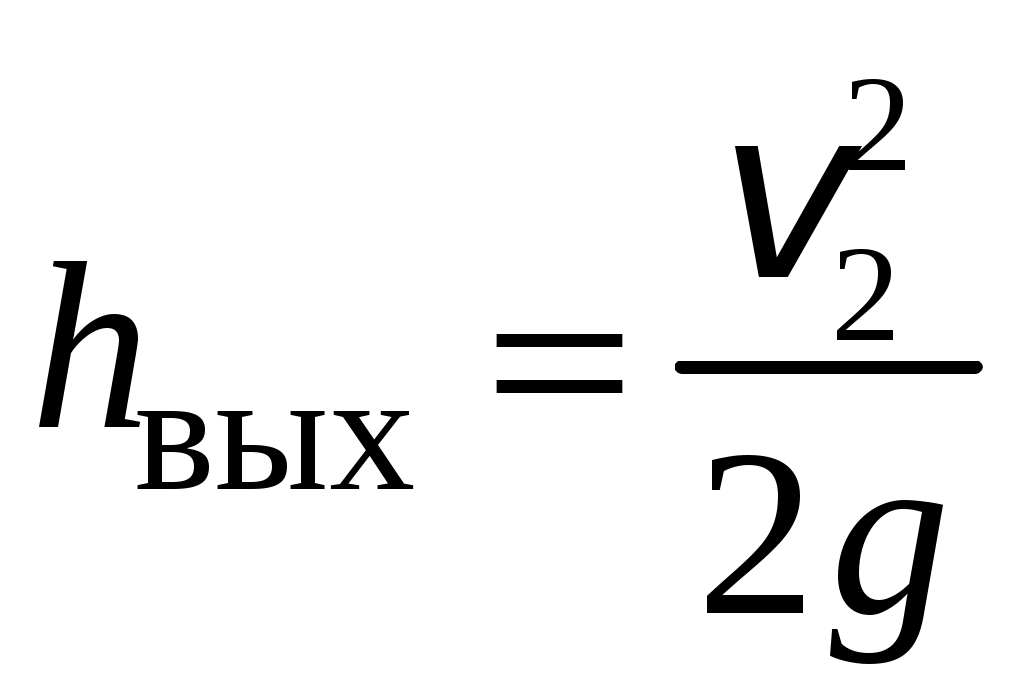 — потери на выходе из диффузора в бак, определяемые по формуле Вейсбаха, в которой v2 — средняя скорость на выходе из диффузора (показана на рисунке, часто встречающаяся ошибка — использовать скорость из другого сечения), коэффициент сопротивления принят равным единице в предположении турбулентного режима течения (при расположении контрольного сечения на выходе диффузора, что возможно, например, в случае истечения в атмосферу, данные потери отсутствуют, но, зато, величина скоростного напора — потери на выходе из диффузора в бак, определяемые по формуле Вейсбаха, в которой v2 — средняя скорость на выходе из диффузора (показана на рисунке, часто встречающаяся ошибка — использовать скорость из другого сечения), коэффициент сопротивления принят равным единице в предположении турбулентного режима течения (при расположении контрольного сечения на выходе диффузора, что возможно, например, в случае истечения в атмосферу, данные потери отсутствуют, но, зато, величина скоростного напора 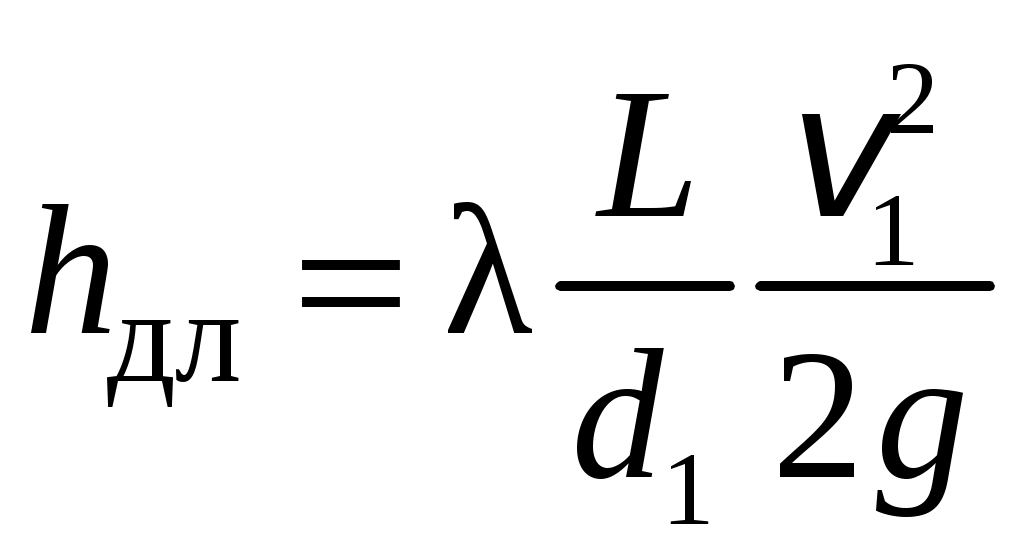 — потери по длине трубопровода с суммарной длиной L, определяемые по формуле Дарси-Вейсбаха, в которой λ — коэффициент гидравлического трения (диаметр d1 указан в условиях задачи; обозначение v1 названо выше). — потери по длине трубопровода с суммарной длиной L, определяемые по формуле Дарси-Вейсбаха, в которой λ — коэффициент гидравлического трения (диаметр d1 указан в условиях задачи; обозначение v1 названо выше).По формуле Борда имеем: 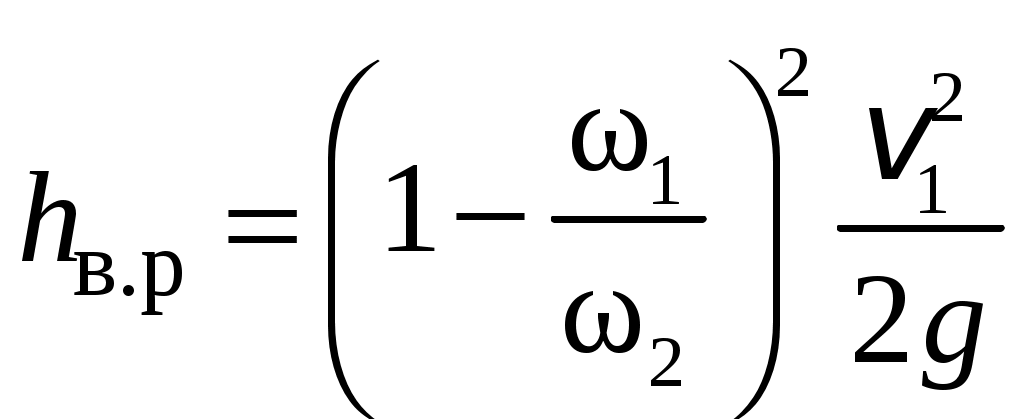 (4) (4)где 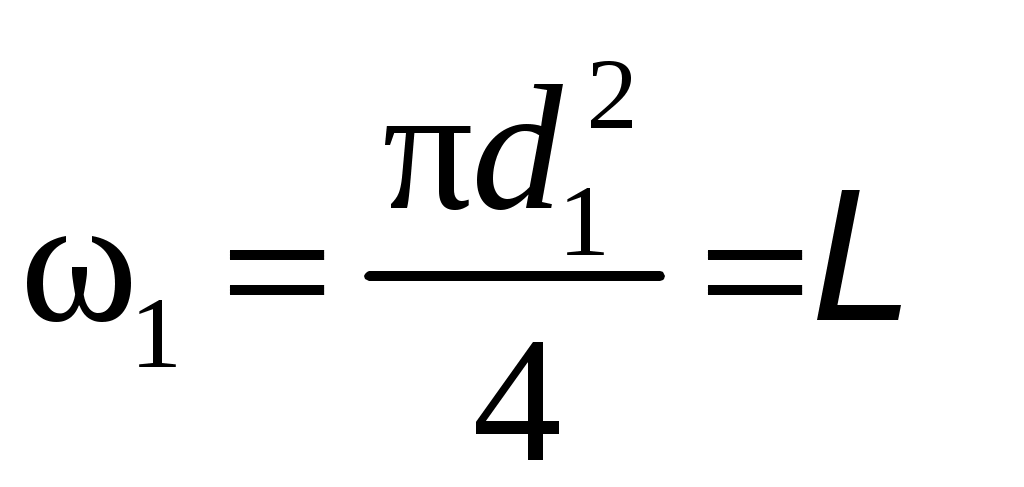 (выполняется численный расчет) — площадь живого сечения на входе в диффузор, одновременно являющаяся площадью проходного сечения трубопровода (диаметр d1 задан в условиях задачи); (выполняется численный расчет) — площадь живого сечения на входе в диффузор, одновременно являющаяся площадью проходного сечения трубопровода (диаметр d1 задан в условиях задачи);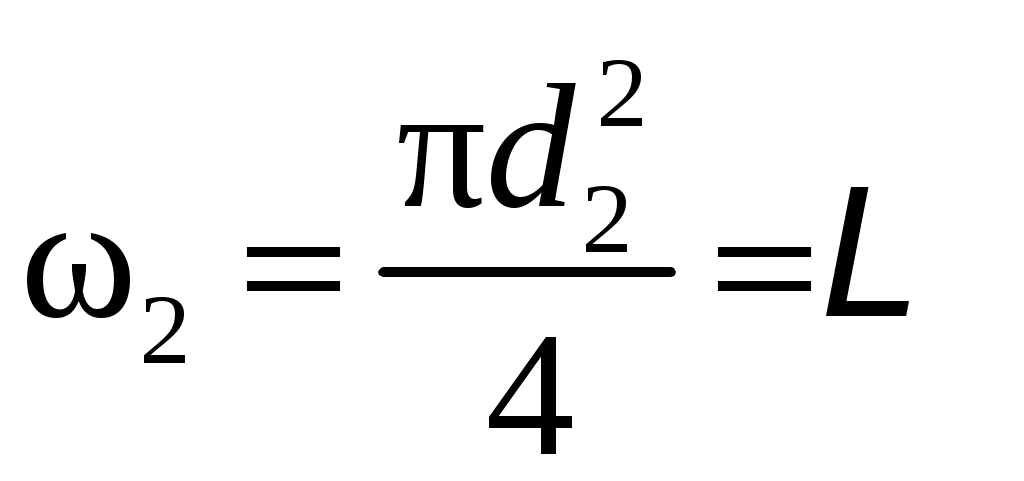 (выполняется численный расчет) — площадь живого сечения на выходе диффузора (диаметр d2 задан в условиях задачи). (выполняется численный расчет) — площадь живого сечения на выходе диффузора (диаметр d2 задан в условиях задачи).Приведенные выше выражения содержат две скорости v1 и v2. В таких случаях с целью сокращения числа неизвестных следует одну скорость выразить через другую по уравнению неразрывности. Уравнение неразрывности и взаимосвязь средней скорости с расходом: Отсюда получим: 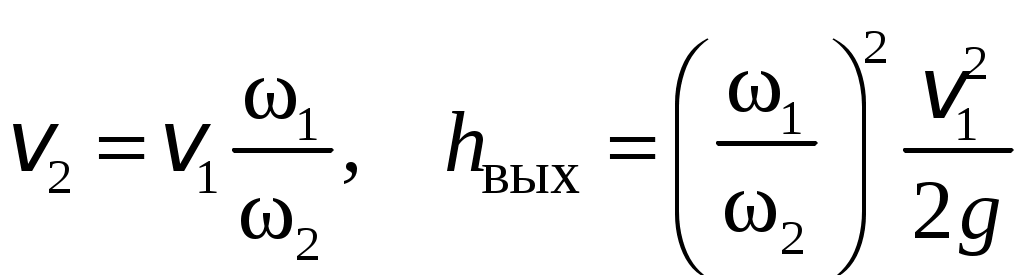 , (6) , (6)Используя выражения (3) (4) и (6), получим 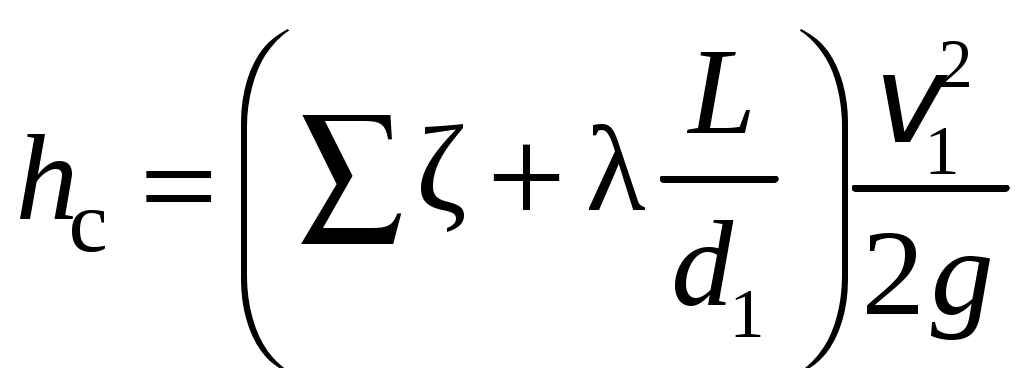 , (7) , (7)где 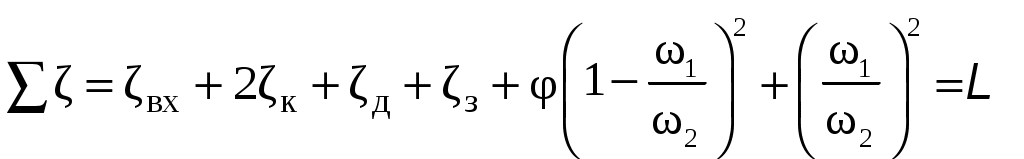 (выполняется численный расчет). (выполняется численный расчет).В данной задаче расход жидкости задан, поэтому можно сразу определить число Рейнольдса и коэффициент гидравлического трения — если расход или диаметр трубопровода неизвестны, то следует, задавшись четвертой зоной потерь по длине, использовать формулу Шифринсона ( 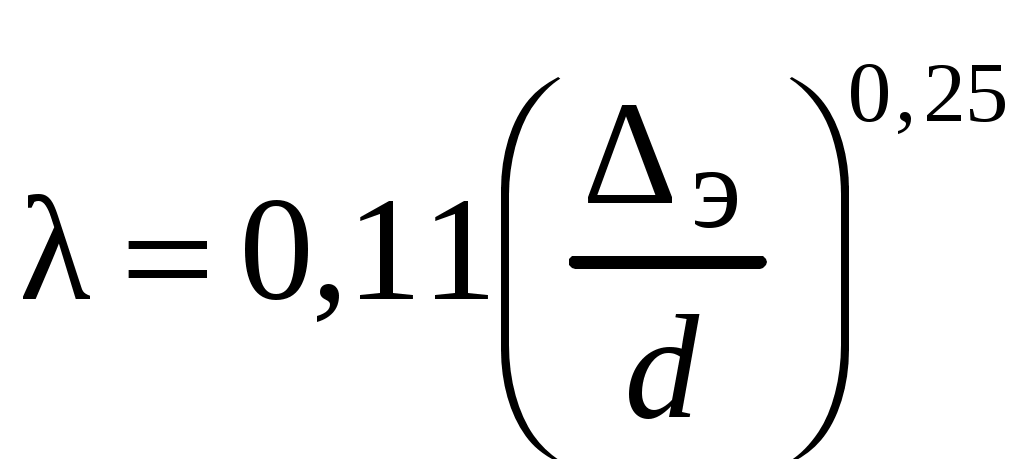 ) и далее выполнить итерационные или графические расчеты в соответствии с методикой по п. 7.2.1, Л7. ) и далее выполнить итерационные или графические расчеты в соответствии с методикой по п. 7.2.1, Л7.Зависимость средней скорости от расхода: 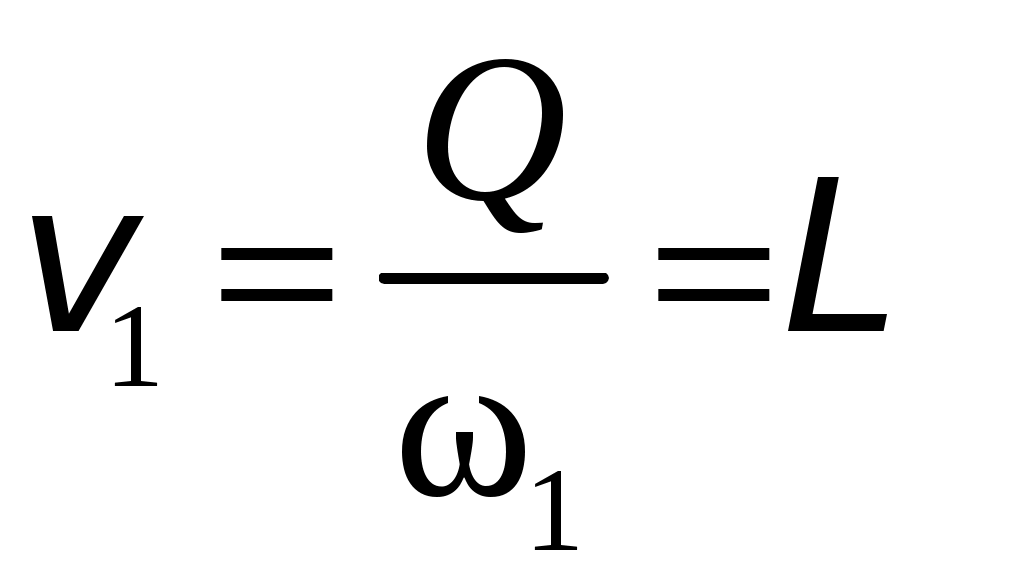 (выполняется численный расчет) (8) (выполняется численный расчет) (8)Число Рейнольдса равно: 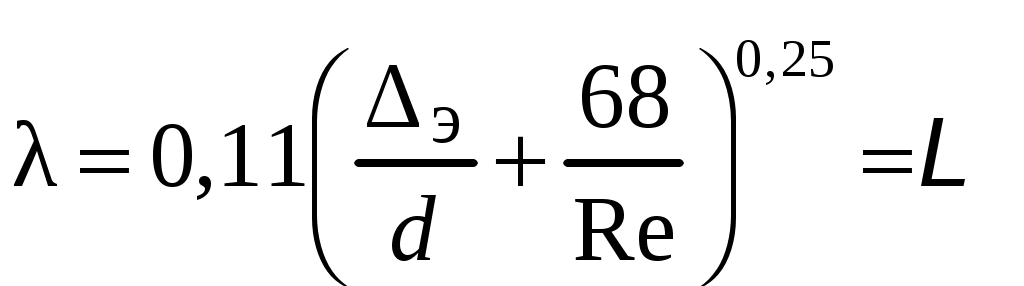 (выполняется численный расчет) (9) (выполняется численный расчет) (9)Подставив численные значения в выражение (7), получим: hc = … (выполняется численный расчет). 6. В данной задаче все величины, входящие в уравнение Бернулли (2), численно определены. Поэтому окончательное решение из данного уравнения получаем без выполнения каких-либо дополнительных расчетов. Подставив в уравнение (2) полученное значение hс и указанные в условиях значения других величин, найдем: 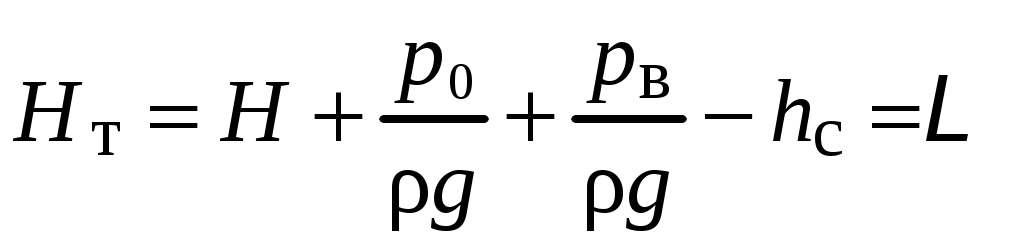 (выполняется численный расчет). (10) (выполняется численный расчет). (10)Ответ: Hт = … |
