РГР2. Гидродинамика
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
Гидродинамика Основным уравнением гидродинамики является уравнение Бернулли. Его составляют для двух живых сечений потока, и для установившегося движении реальной жидкости, оно имеет следующий вид: 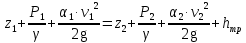 где 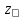 – геометрический напор или высота положения — расстояние от произвольно выбранной горизонтальной плоскости сравнения до центра тяжести сечении (в энергетическом смысле — это удельная, т. е. отнесенная к единице веса жидкости, потенциальная энергия положении); р – давление в центре тяжести сечения; – геометрический напор или высота положения — расстояние от произвольно выбранной горизонтальной плоскости сравнения до центра тяжести сечении (в энергетическом смысле — это удельная, т. е. отнесенная к единице веса жидкости, потенциальная энергия положении); р – давление в центре тяжести сечения; 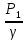 –пьезометрический напор — вертикальное расстояние между центром тяжести сечения и уровнем жидкости в пьезометре (удельная потенциальная энергия давления); –пьезометрический напор — вертикальное расстояние между центром тяжести сечения и уровнем жидкости в пьезометре (удельная потенциальная энергия давления); 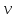 — средняя скорость потока в сечении; — средняя скорость потока в сечении; 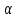 — коэффициент Кориолиса (отношение действительной кинетической энергии потока к условной кинетической энергии, вычисленной по средней скорости); — коэффициент Кориолиса (отношение действительной кинетической энергии потока к условной кинетической энергии, вычисленной по средней скорости); 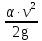 — скоростной напор (удельная кинетическая энергия); — скоростной напор (удельная кинетическая энергия); 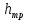 — гидравлические потери напора (та часть удельной механической энергии, которую жидкость теряет на преодоление сопротивлений на участке потока между сечениями 1 и 2). Вследствие работы сил трения она превращается в тепловую энергию и рассеивается в пространстве. Уравнение Бернулли является частным случаем закона сохранения энергии. — гидравлические потери напора (та часть удельной механической энергии, которую жидкость теряет на преодоление сопротивлений на участке потока между сечениями 1 и 2). Вследствие работы сил трения она превращается в тепловую энергию и рассеивается в пространстве. Уравнение Бернулли является частным случаем закона сохранения энергии. Как видно, уравнение Бернулли выражает связь между тремя разными параметрами потока: высотой положения z, давлением р и средней скоростью 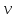 . .При решении практических задач вместе с уравнением Бернулли применяется и уравнение неразрывности, т.е. равенства расхода Q во всех сечениях установившегося потока: 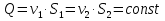 Из него следует, что средние скоростиv обратно пропорциональны площадям живых сечений. При использовании уравнения Бернулли целесообразно руководствоваться следующим:
Потери энергии зависят от скорости движения жидкости, от формы и размера русла и от вязкости жидкости. Т.к. в большинстве случаев потери энергии приблизительно пропорциональны квадрату скорости, то их определяют по формуле: 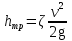 Потери энергии разделяются на местные и потери энергии по длине потока. Местные потери энергии обусловлены местными сопротивлениями. В них происходит изменение формы потока и обычно наблюдается интенсивные вихреобразные. Потери энергии на трение по длине трубы определяют по формуле Дарси: 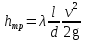 где �� – коэффициент гидравлического сопротивления; l – длина расчетного участка трубы; d – диаметр трубы. Имеется ряд формул для определения коэффициента �� в зависимости от числа Рейнольдса 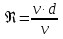 1. Зона вязкого сопротивления, соответствует режиму ламинарного течения. 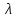 определяется по формуле Пуазеля определяется по формуле Пуазеля 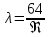 , при R , при R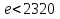 2. Область гладкостенного сопротивления. Здесь толщина ламинарного слоя δ больше толщины бугорков шероховатости 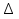 . Коэффициент . Коэффициент 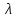 не зависит от шероховатости и определяется по формуле Блазиуса: не зависит от шероховатости и определяется по формуле Блазиуса: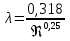 , при , при 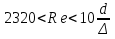 3. Зона перехода от гладкостенного к квадратичному сопротивлению. В ней 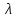 зависит и от числа Рейнольдса и от относительной шероховатости. зависит и от числа Рейнольдса и от относительной шероховатости. 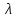 определяется по формуле Альтшуля определяется по формуле Альтшуля 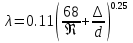 , при , при 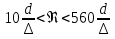 4. Зона квадратичного сопротивления. Здесь 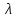 не зависит и от числа Рейнольдса, а зависит лишь от относительной шероховатости. не зависит и от числа Рейнольдса, а зависит лишь от относительной шероховатости. 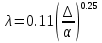 , при 56 , при 56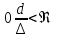 Расход жидкости при ее истечении через отверстие или насадок определяется по формуле 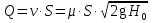 или или 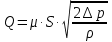 где μ — коэффициент расхода, S — площадь отверстия или сечения насадка; Но — действующий напор, равный: 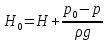 где Н — расстояние от центра тяжести отверстия или сечения насадка до поверхности жидкости в резервуаре; ро — давление на поверхности жидкости в сосуде; р — давление в среде, в которую происходит истечение жидкости; Δр — потери давления при истечении через местное сопротивление (например, через дроссель, распределитель и другую гидравлическую аппаратуру). Коэффициент расхода μ малого отверстия зависит от числа Рейнольдса. С увеличением Re коэффициент μ сначала увеличивается, достигает максимального значения μмакс = 0,69 при Re = 350, а затем начинает уменьшаться и стабилизируется на значении, равном 0,60. Таким образом, отверстия (а также насадки) при больших числах Re удобно применять в качестве приборов для измерения расхода жидкости. При истечении жидкости через затопленное отверстие или насадок для определения расхода применяется приведенная формула (17), но в этом случае напор Но берется как разность гидростатических напоров по обе стороны стенки. Следовательно, расход в данном случае не зависит от высоты расположения отверстия или насадка. В случае истечения жидкости через насадок образуется вакуум, который увеличивает его пропускную способность и является прямо пропорциональным напору Hо. Коэффициент расхода насадка зависит от его типа и числа Рейнольдса. По своему значению он превышает коэффициент расхода малого отверстия. Например, для внешнего цилиндрического насадка μ = 0,80, для коноидального насадка μ = 0,96 - 0,99. Задача 2.1. Из напорного бака вода течет по трубе диаметром d1=20 мм и затем вытекает в атмосферу через насадок (брандспойт) с диаметром выходного отверстия d2 = 10 мм. Избыточное давление воздуха в баке ро = 0,18 МПа; высота H= 1,6 м. Пренебрегая потерями энергии, определить скорости течения воды в трубе V1и на выходе из насадка V2. Задача 2.2. Определить расход керосина, вытекающего из бака по трубопроводу диаметром d = 50 мм, если избыточное давление воздуха в баке р0= 16 кПа; высота уровня Hо= 1 м; высота подъема керосина в пьезометре, открытом в атмосферу, H= 1,75 м. Потерями энергии пренебречь. Плотность керосина ρ= 800 кг/м3. 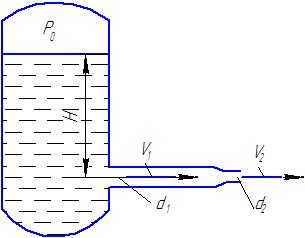 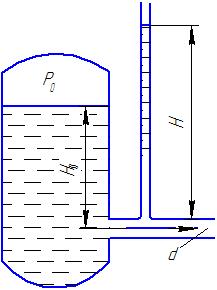 Рис. 2.1. Рис.2.2. Задача 2.3. К расходомеру Вентури присоединены два пьезометра и дифференциальный ртутный манометр. Выразить расход воды Qчерез размеры расходомера Dи d, разность показаний пьезометров ΔH, а также через показание дифференциального манометра Δh. Дан коэффициент сопротивления ζ участка между сечениями 1—1 и 2—2. Задача 2.4. Определить весовой расход воздуха по трубе с плавно закругленным входом и цилиндрической частью диаметром D = 200 мм, если показание вакуумметра в виде вертикальной стеклянной трубки, опущенной в сосуд с водой h = 250 мм. Коэффициент сопротивления входной части трубы (до места присоединения вакуумметра) ζ = 0,1. Плотность воздуха ρвоз=1,25 кг/м3. 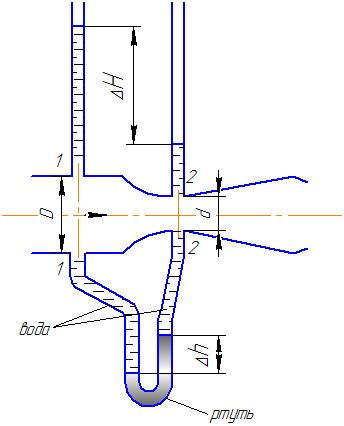 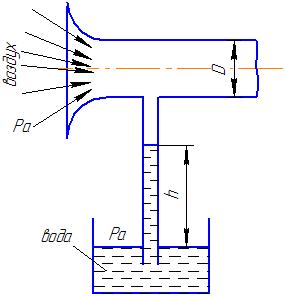 Рис. 2.3. Рис.2.4. Задача 2.7. Жидкость вытекает из открытого резервуара в атмосферу через трубу, имеющую плавное сужение до диаметра d1, а затем постепенное расширение до d2.. Истечение происходит под действием напора H = 3 м. Пренебрегая потерями энергии, определить абсолютное давление в узком сечении трубы 1—1, если соотношение диаметров d2/d1 = 2; плотность жидкости ρ=1000 кг/м3. Найти напор Hкр, при котором абсолютное давление в сечении 1–– 1 будет равно нулю. Задача 2.8. Вода перетекает из напорного бака, где избыточное давление воздуха р = 0,3 МПа, в открытый резервуар по короткой трубе диаметром d = 50 мм, на которой установлен кран. Чему должен быть равен коэффициент сопротивления крана для того, чтобы расход воды составлял Q = 8,7 л/с? Высоты уровней H1 = l м и H2 = 3 м. Учесть потерю напора на входе в трубу (ζвх = 0,5) и на выходе из трубы (внезапное расширение). 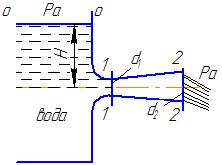 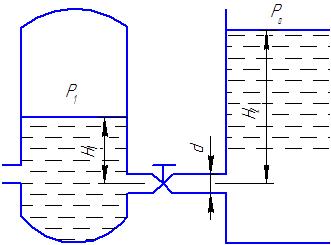 Рис. 2.7. Рис.2.8. Задача 2.9. Определить расход нефти (γ=8,35 кН/м ) и напор в баке без учета потерь напора, если заданы диаметры трубопровода d1 и d2, а также перепад уровней ртутиh в дифманометре (d1=50 мм, d2=30 мм, h=60 мм рт. ст.). Задача 2.10.Определить показание дифференциаль ного манометра и напор в бакеН без учета потерь, если диаметры трубопроводаd1 и d2 и расход воды Q, причем, d1=60 мм, d2=25 мм, Q=5 л/с. Задача 2.11.Определить диаметр трубопровода d1 и напор в бакеН без учета потерь напора, если заданы диаметрd2, расход водыQ и перепад ртутиh в дифференциальном манометре (d2=40 мм, Q=6 л/с, h=70 мм рт. ст.). Задача 2.12.Определить скорость течения водыV2 (рис. 63) и расходQ в трубке, если d1=95 мм, d2=50 мм, h=100 см. 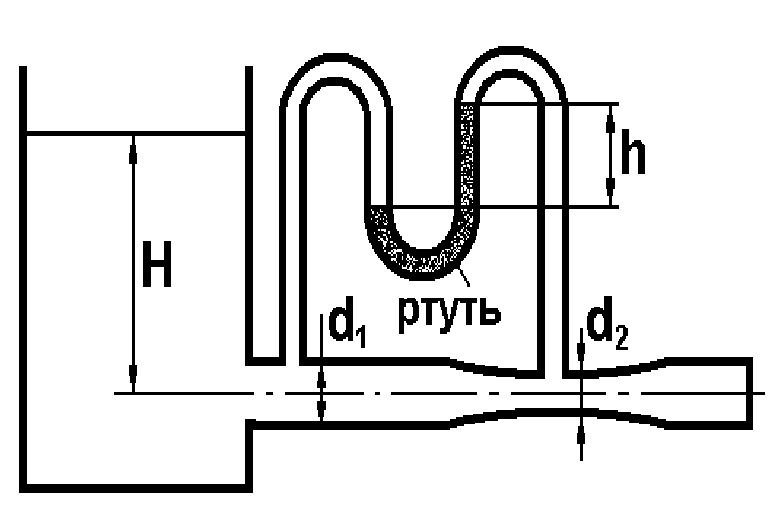 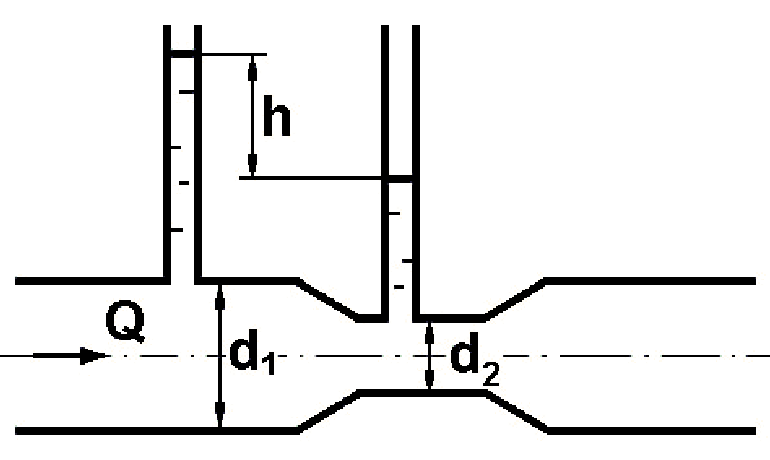 Рис. 2.9., 2,10., 2,11 Рис.2.12. Задача 2.13. Определить расход воды, вытекающей из бака через короткую трубку (насадок) диаметром d = 30 мм и коэффициентом сопротивления ζ = 0,5, если показание ртутного манометра hрт=1,47 м; H1 = l м; H0=1,9 м; l = 0,1 м. Задача 2.14. При внезапном расширении трубы от d до D получается увеличение давления, которому соответствует разность показаний пьезометров ΔН. Определить, при каком соотношении площадей широкого и узкого сечений трубы увеличение давления будет наибольшим. 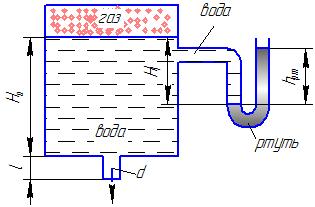 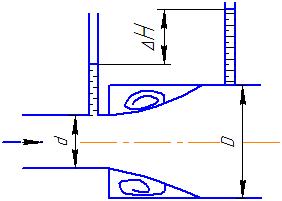 Рис. 2.13. Рис.2.14. Задача 2.15. Вода перетекает из напорного бака А в резервуар Б через вентиль с коэффициентом сопротивления ζв=3 по трубе. Диаметры: d1=40 мм; d2 = 60 мм. Считая режим течения турбулентным и пренебрегая потерями на трение по длине, определить расход. Учесть потери напора при внезапных сужениях и расширениях. Высоты: Н1 = l м, H2 = 2 м; избыточное давление в напорном баке ро = 0,15 МПа. 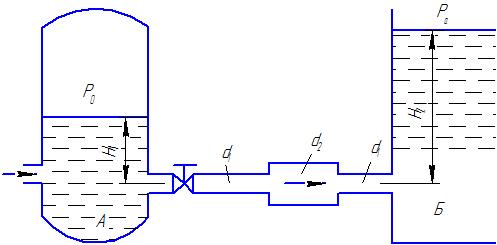 Рис. 2.15 Задача 2.16. По длинной трубе диаметром d = 50 мм протекает жидкость (ν = 2 Ст; ρ = 900 кг/м3). Определить расход жидкости и давление в сечении, где установлены пьезометр (h = 60 см) и трубка Пито (H = 80 см). Задача 2.17. На рисунке показана схема двойного диффузора карбюратора, который обеспечивает больший вакуум, чем одинарный. Выходное сечение малого и узкое сечение большого диффузоров совпадают; в узком сечении малого диффузора расположен обрез распылителя бензина (наклонная трубка). Определить величину разрежения в сечении 1 — 1 при расходе воздуха G = 2 Н/с и следующих размерах: D = 40 мм; d1 = 12 мм; d2 = 20 мм. Принять следующие значения коэффициентов сопротивления участков воздушного потока: от 0—0 при ро=ра и v = 0 до 1—1 ζ1 = 0,1; от 1— 1 до 2—2 (внутри малого диффузора) ζ2 = 0,2 (отнесены к площади πd12/4); от 0—0 до 2—2 (горловины большого диффузора) ζ3 = 0,12 (отнесено к площади π (D2—d22)/4). Воздух считать несжимаемым, плотность ρвоз = 1,25 кг/м3. Давление в горловине большого диффузора (2—2) считать равным давлению на выходе из малого диффузора. 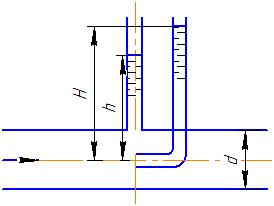 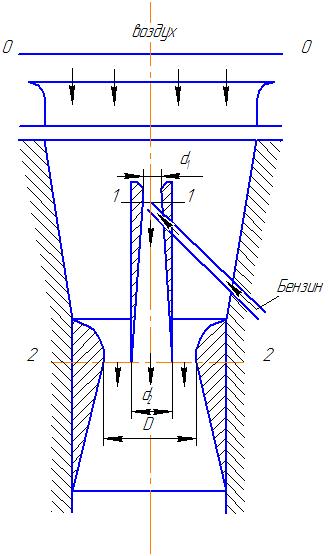 Рис. 2.16. Рис.2.17. Задача 2.17. Определить расход воды через сифон, если Н1=0,85 м, Н2=1,8 м, Н3=3,7 м, общая длина сифона l=23 м, диаметр d=25 мм. Учесть местные потери и потери по длине, ��=0,03. Температура воды t=20оС, сифон стальной,R=d. Задача 2.18. Определить абсолютное давление перед входом в насос. Подача насоса Q=2,3 л/с, l=1,5 м, d=40 мм, tМАСЛА=60оС. Давление в баке ра=266,8 мм рт.ст. Коэффициент сопротивления крана ζkp=1,5, коэффициент сопротивления входа в трубу ζВх=0,5, высота уровня масла в баке над сечением входа в насос Н=1,2 м, масло индустриальное И-12. 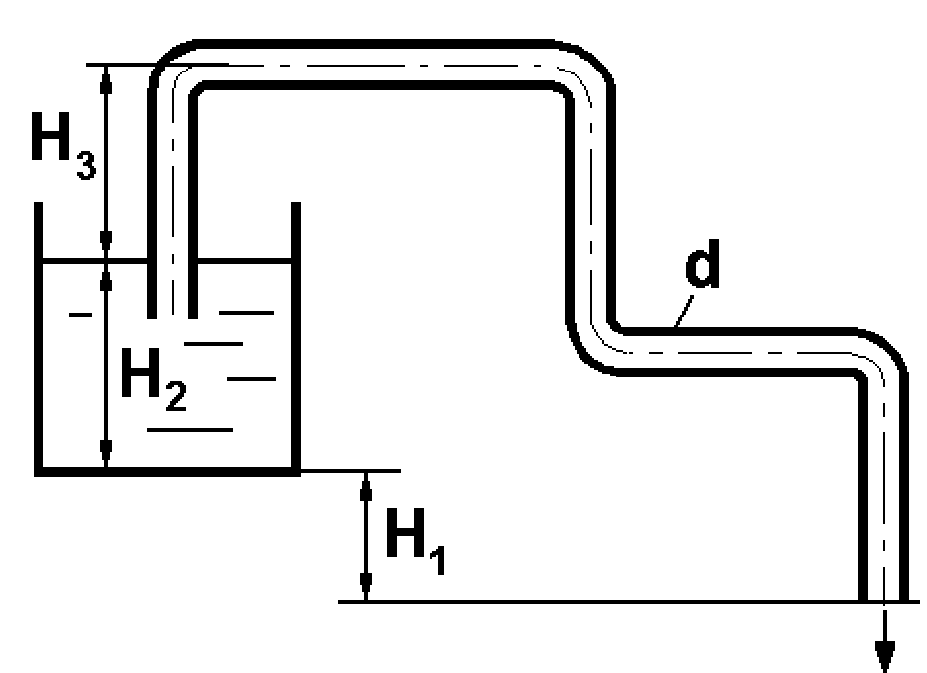 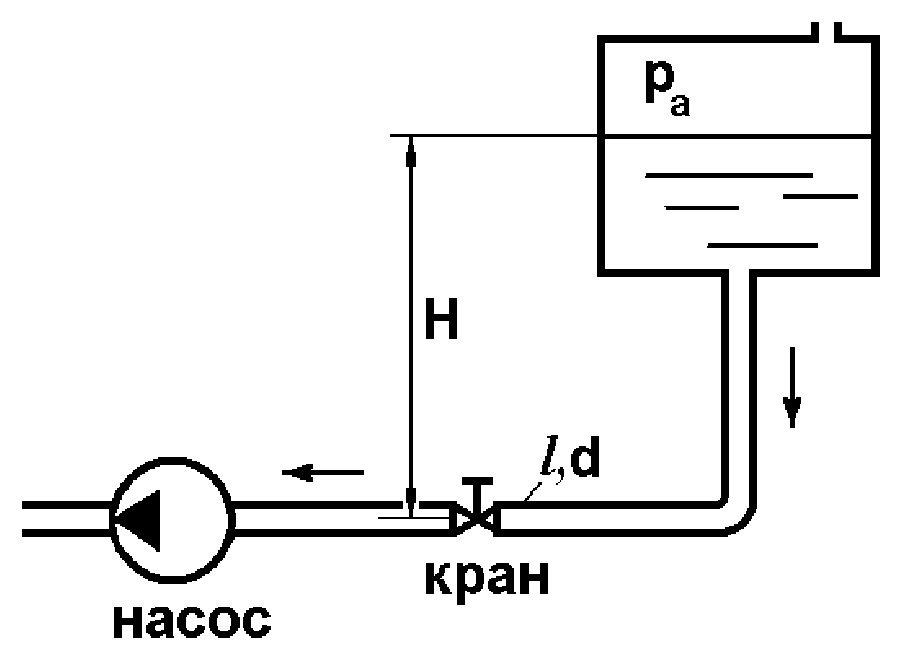 Рис. 2.17 Рис. 2.18 Задача 2.19. Определить напор воды Н в баке с учетом всех сопротивлений, если ро=80 кПа, расход воды Q=1,3 л/с, длины участков:l1=2 м, l2=1,5 м, l3= 1м; диаметры:d1=25 мм, d2=40 мм, d3=20 мм, d4=10 мм, материал труб - алюминий, lВОдЫ=15оС. Коэффициент сопротивления сопла принять равным ζСОП=0,05. Задача 2.20. Вычислить скорость истечения воды через отверстие и опреде лить расход, если Н=1,8 м, ро=100 кПа, d=10 мм. Выяснить, как изменится расход, если подсоединить к отверстию цилиндрический насадок. Задача 2.21. Из закрытого бака через цилиндрический насадок вода вытекает в промежуточную емкость, а из нее через отверстие в атмосферу. Найти уровень воды в открытом резервуаре Z2, если ро=180 кПа, z1=2,5 м, d1=15 мм, d2=20 мм. 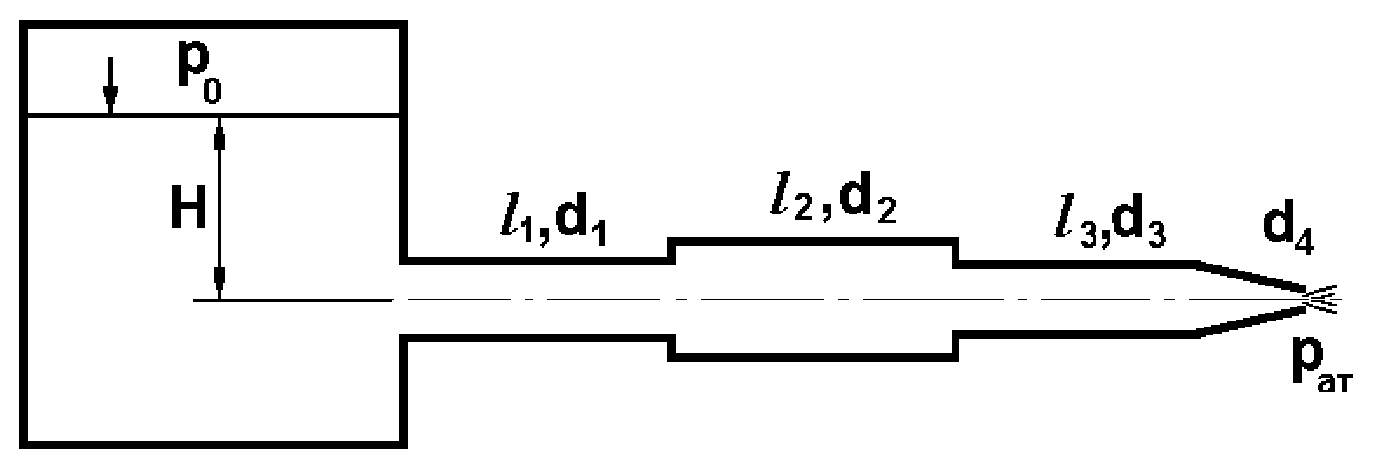 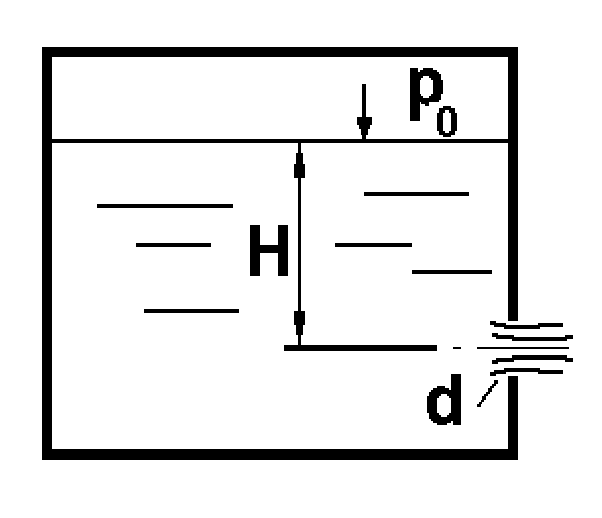 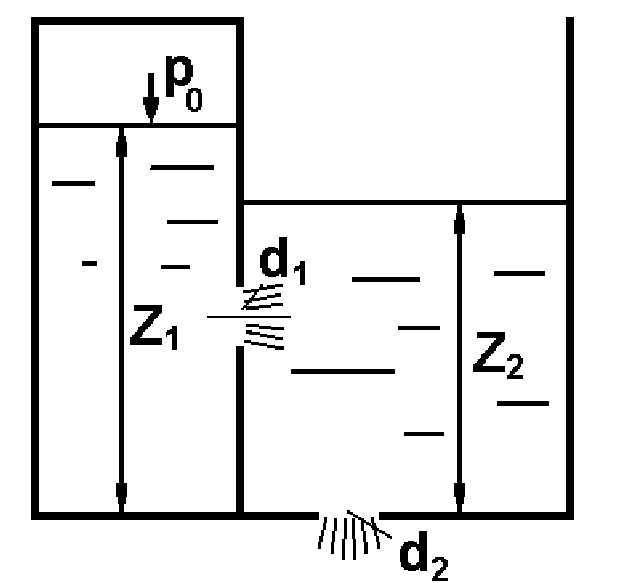 Рис. 2.19 Рис. 2.20 Рис. 2.21 Задача 2.22. В баке имеется перегородка с отверстием (d=100 мм), в него поступает вода в количестве Q=60 л/с. Из каждой секции вода вытекает через цилиндрический насадок (dHAC= d). Определить расход через каждый насадок, если μОТВ=0,62,μнас=0,82. Задача 2.23. Определить суммарный расход воды через два отверстия в стенке резервуара: круглое (d=50 мм), расположенное на расстоянии h1=1,2 м от дна и расположенное у дна. Каков будет суммарный расход Q, если к верхнему отверстию присоединить цилиндрический насадок (Н=2,4 м)? Задача 2.24. В вертикальной стенке, разделяющей резервуар на две части, рас положено круглое отверстие (d1=60 мм, Н1=2,7 м, расход через отверстие Q=3,3 л/с). Определить глубину Н2 воды в правой части, диаметр d2 отверстия в наружной стенке и скорость струи Vc в сжатом сечении струи, вытекающей из резервуара, если l=1,2 м. 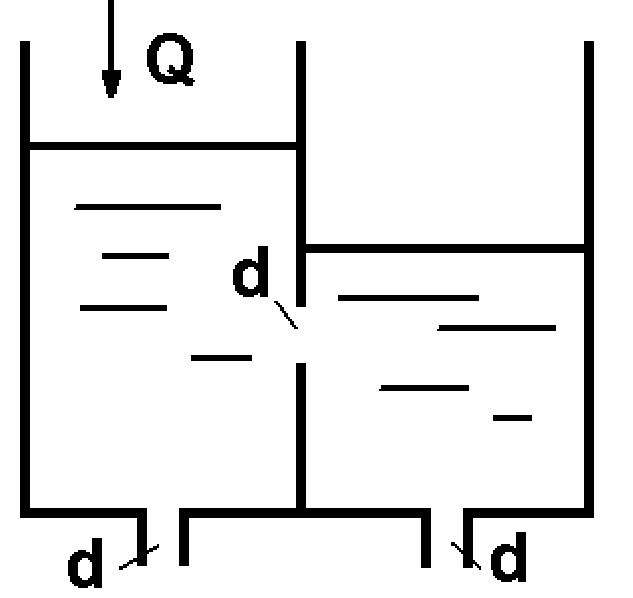 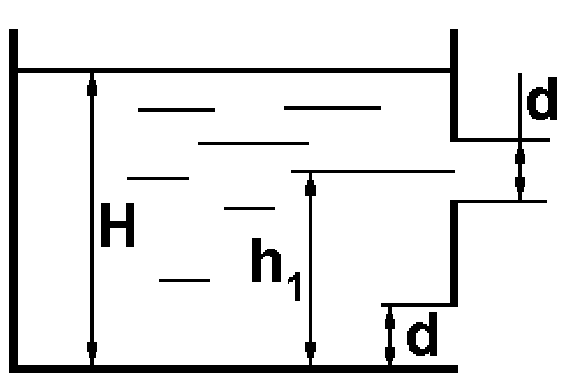 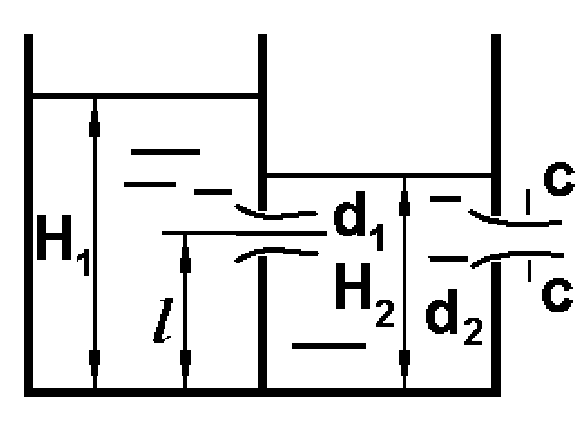 Рис. 2.22 Рис. 2.23 Рис. 2.24 |
