Реферат. Глобальные компьютерные сети
 Скачать 327.25 Kb. Скачать 327.25 Kb.
|
Наиболее известной глобальной сетью является Интернет. Для доступа в Интернет используется модем. Но сегодня появляется все больше компьютеров с выходом в Интернет через локальную сеть.На данный момент существует большая разновидность подключения к Internet, это подключение и по выделенной линии, через спутник, ну и по телефонной линии через модем(Dial -Lab).Соединения по выделенной линии - самые распространенные. Скорость при подключении на такой линии составляет 100Мбит/с, в то время как у Dial-lab 56Кбит/с.. Практическая (расчетная) часть Задача № 1 Тема Информация, кодирование информации Состоит из 2 частей Часть 1 Задания к вариантам работы 1. Переведите данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления. 2. Переведите данное число в десятичную систему счисления. 3. Сложите числа. 4. Выполните вычитание. 5. Выполните умножение. Примечание: в заданиях 3 — 5 проверьте правильность вычислений переводом исходных данных и результатов в десятичную систему счисления. В задании 1 д) получите пять знаков после запятой в двоичном представлении. Вариант 10 1. а) 618(10); б) 928,25(10); в) 155,45(10). 2. а) 1111011011(2); б) 1001110110,011(2); в) 1011110011,10111(2); г) 675,2(8); е) 94,4(16). 3. а) 11111010(2) + 10000001011(2); б) 1706,34(8) + 650,3(8); в) 180,4(16) + ЗА6,28(16). 4. а) 111101101(2) - 101111010(2); б) 1300,44(8) - 1045,34(8); в) 16А,8(16) - 147,6(16). 5. а) 100111(2) · 110101(2); б) 1542,2(8) · 50,6(8); в) А,8(16) · Е,2(16). Решение 1. а)Делим число 618 на основание системы счисления = 2: 618 / 2 = 309 остаток 0; 309 / 2 = 154 остаток 1; 154 / 2 = 77 остаток 0; 77 / 2 = 38 остаток 1; 38 / 2 = 19 остаток 0; 19 / 2 = 9 остаток 1; 9 / 2 = 4 остаток 1; 4 / 2 = 2 остаток 0; 2 / 2 = 1 остаток 0. Дальше делить нельзя, поэтому собираем все остатки, начиная с конца, и учитываем конечный результат от деления т.е. 2 / 2 = 1 Получим число: 1001101010 б) Переводим целую часть числа Делим число 928 на основание системы счисления = 2: 928 / 2 = 464 остаток 0; 464 / 2 = 232 остаток 0; 232 / 2 = 116 остаток 0; 116 / 2 = 58 остаток 0; 58 / 2 = 29 остаток 0; 29 / 2 = 14 остаток 1; 14 / 2 = 7 остаток 0; 7 / 2 = 3 остаток 1; 3 / 2 = 1 остаток 1 Дальше делить нельзя, поэтому собираем все остатки, начиная с конца, и учитываем конечный результат от деления т.е. 3 / 2 = 1 Получим число: 1110100000 Перевод дробной части числа Определяем 1-й знак после запятой: Умножаем 25 * 2 = 50 => [0] 50; Определяем 2-й знак после запятой: Умножаем 50 * 2 = 100 => [1] 00 Дробную часть числа нашли: 01 Все число = 1110100000,01 в) Переводим целую часть числа Делим число 155 на основание системы счисления = 2: 155 / 2 = 77 остаток 1;77 / 2 = 38 остаток 1; 38 / 2 = 19 остаток 0; 19 / 2 = 9 остаток 1; 9 / 2 = 4 остаток 1; 4 / 2 = 2 остаток 0; 2 / 2 = 1 остаток 0 Дальше делить нельзя, поэтому собираем все остатки, начиная с конца, и учитываем конечный результат от деления, т.е. 2 / 2 = 1 Получим число: 10011011 Перевод дробной части числа Определяем 1-й знак после запятой: Умножаем 45 * 2 = 90 => [0] 90 Определяем 2-й знак после запятой: Умножаем 90 * 2 = 180 => [1] 80 Определяем 3-й знак после запятой: Умножаем 80 * 2 = 160 => [1] 60 Определяем 4-й знак после запятой: Умножаем 60 * 2 = 120 => [1] 20 Определяем 5-й знак после запятой: Умножаем 20 * 2 = 40 => [0] 40 Дробную часть числа нашли: 01110 Все число = 10011011,01110 2. а) Перевод числа 1111011011 из 2-й в 10-ую систему счисления Сначала напишем разряды символов числа: 1 1 1 1 0 1 1 0 1 1 - само число 9 8 7 6 5 4 3 2 1 0 - разряды числа Начнём перевод числа: 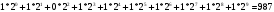 б) Перевод числа 10011011,01110 из 2-й в 10-ую систему счисления Сначала напишем разряды символов числа: 1 0 0 1 1 0 1 1, 0 1 1 1 0 - само число 7 6 5 4 3 2 1 0 -1 -2 -3 -4 -5 - разряды числа Начнём перевод числа: 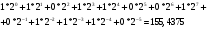 Вычисление записывали в следующем порядке: с нулевого разряда в лево - целая часть; с минус первого разряда в право - дробная часть. 3. а) 11111010(2) + 10000001011(2)= 10100000101(2) б) 1706,34(8) + 650,3(8)= 2556,64(8) в) 180,4(16) + 3А6,28(8)= 526,68(8) Проведем проверку а) 11111010(2)= 250(10); 10000001011(2)= 1035(2); 10100000101 (2)= 1285(10) б) 1706,34(8) = 966,4375(10); 650,3(8)= 424,375(10); 2556,64(8)= 1390,8125(10) в) 180,4(16) = 384,25(10); 3A6,28(16)= 934,15625(10); 526,68(16)= 1318,40625(10) 4. а)111101101(2) - 101111010(2)= 1110011(2) б) 1300,44(8) - 1045,34(8)= 233,2(8) в) 16А,8(16) - 147,6(16)= 23,2(16) Проведем проверку а) 111101101(2) =493; 101111010(2)= 378; 1110011(2)= 115 б) 1300,44(8) =704,5625; 1045,34(8)= 549,4375; 233,2(8)=155,125 в) 16А,8(16) = 362,5(10) ; 147,6(16)= 327,375(10); 23,2(16)= 35,125(10) 5. а) 100111(2) · 110101(2)= 100000010011(2) б) 1542,2(8) · 50,6(8)= 234,869140625(8) в) А,8(16) · Е,2(16)=94,5(16) Проведем проверку а) 100111(2) =39(10); 110101(2)=53(10); 100000010011(2)=2067(10) б)1542,2(8)=866,25(10); 50,6(8)=40,75(10); 234,869140625(8)=35299,6875(10) в) А,8(16) =10,5(10); Е,2(16)=14,125(10); 94, (16)5=148,3125(10) Часть 2 Задания к вариантам работы 1. Переведите данное число из десятичной системы счисления в двоично-десятичную. 2. Переведите данное число из двоично-десятичной системы счисления в десятичную. 3. Зашифруйте данный текст, используя таблицу ASCII-кодов. 4. Дешифруйте данный текст, используя таблицу ASCII-кодов. 5. Запишите прямой код числа, интерпретируя его как восьмибитовое целое без знака. 6. Запишите дополнительный код числа, интерпретируя его как восьмибитовое целое со знаком. 7. Запишите прямой код числа, интерпретируя его как шестнадцатибитовое целое без знака. 8. Запишите дополнительный код числа, интерпретируя его как шестнадцатибитовое целое со знаком. 9. Запишите в десятичной системе счисления целое число, если дан его дополнительный код. 10. Запишите код действительного числа, интерпретируя его как величину типа Double. 11. Дан код величины типа Double. Преобразуйте его в число. Вариант 10 1. а) 817(10); б) 661(10); в) 491(10). 2. а) 100001010001(2--10); б) 010000000111(2--10); в) 001001110001(2--10). 3. Принтер. 4. 42 69 6Е 61 72 79. 5. а) 219(10); б) 240(10); в) 202(10). 6. а) 44(10); б) -43(10); в) -94(10). 7. а) 23359(10); б) 27428(10). 8. а) 21481(10); б) -20704(10). 9. а) 0001101010101010; б) 1011110111001011. 10. а) -141,375; б) 145,375. 11. а) 408ЕА14000000000; б) С07В128000000000. Решение 1. Для выполнения воспользуемся таблицей (табл.1)
Таблица1. Двоичные коды десятичных и шестнадцатеричных цифр а) 817(10)= 100000010111(2--10) б) 661(10)= 011001100001(2--10) в) 491(10)=010010010001(2--10) 2. а) 1000.0101.0001(2--10)= 851(10) б) 0100.0000.0111(2--10)= 407(10) в) 0010.0111.0001(2--10)=271(10) 3. Воспользуемся следующими таблицами ASII кодов (табл.2) 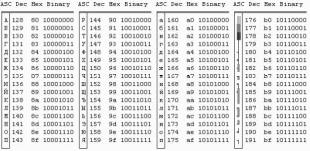 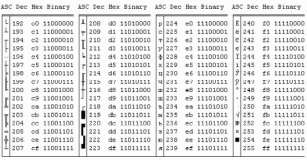 8f e0 a8 ad e2 a5 e0 Таблица 2. ASII коды 4. Воспользуемся таблицей ASCII кодов (табл.3) 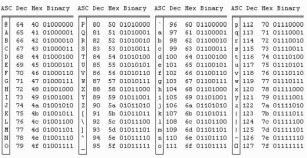 Binary Таблица 3. ASCII коды Binary Таблица 3. ASCII коды5. а) 219(10) = 11011011 б) 240(10) = 11110000 в) 202(10) = 11001010 6. Дополнительный код положительного числа в двоичной системе счисления совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы: а) 44(10)=0|0101100 б) -43(10)= 1|1010101 в) -94(10)=1|0100011 7.а) 23359(10);= 0101101100111111 б) 27428(10)= 0110101100100100 8. а) 21481(10);= 0|101001111101001 б) -20704(10)= 1|010111100111111 9. а) 0001101010101010= +6826; б) 1011110111001011= - 16950 10. а) 141,375=8D,6000000000000. б) 145,375= 91,6000000000000. 11. а) 408ЕА14000000000=67693076 б) С07В128000000000= 201830696 Задача № 2. Вариант 10. Сочетаниями из n элементов по m (m  n) называются неупорядоченные m-элементные выборки из данных n элементов. n) называются неупорядоченные m-элементные выборки из данных n элементов.Ясно, что все сочетания отличаются друг от друга хотя бы одним элементом, а порядок элементов здесь не существенен. Число сочетаний из n по m обозначается 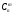 ,чтобы из сочетаний получить размещения, надо упорядочить каждую m-элементную выборку, а это можно сделать m! способами. Следовательно, число сочетаний ,чтобы из сочетаний получить размещения, надо упорядочить каждую m-элементную выборку, а это можно сделать m! способами. Следовательно, число сочетаний 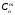 меньше числа размещений меньше числа размещений 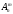 в m! раз. Учитывая этот факт, получим соответствующие формулы для вычисления числа сочетаний: в m! раз. Учитывая этот факт, получим соответствующие формулы для вычисления числа сочетаний: (1) 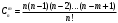 и (2) и (2) 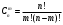 Следовательно, при реализации программы необходимо будет: ввести n и m, ввести необходимые функции, формулы и вывести результат на экран. Блок-схема 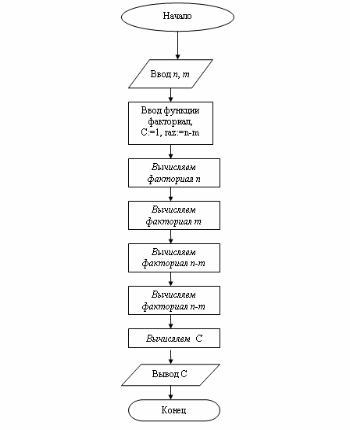 Описание алгоритма на алгоритмическом языке (Pascal) Program example; Var n, m, raz, C: integer; uses crt; function Factorial(i: word): LongInt; begin if i=0 then Factorial := 1 else Factorial := i*Factorial(i-1); end; Begin Readln(n); Readln(m); Raz:=n-m; n:=Factorial(n); m:=Factorial(m); Raz:=Factorial(Raz); C:=n/(m*raz) Writeln(С); End. Задача № 3 Вариант 10 Менеджер по ценным бумагам намерен разместить 100000 ф. ст. капитала таким образом, чтобы получать максимальные годовые проценты с дохода. Его выбор ограничен четырьмя возможными объектами инвестиций А, В, С и О. Объект А позволяет получать 6% годовых, объект В – 8% годовых, объект С – 10%, а объект 0 – 9% годовых. Для всех четырех объектов степень риска и условия размещения капитала различны. Чтобы не подвергать риску имеющийся капитал, менеджер принял решение, что не менее половины инвестиций необходимо вложить в объекты А и В. Чтобы обеспечить ликвидность, не менее 25% общей суммы капитала нужно поместить в объект О. Учитывая возможные изменения в политике правительства, предусматривается, что в объект С следует вкладывать не более 20% инвестиций, тогда как особенности налоговой политики требуют, чтобы в объект А было вложено не менее 30% капитала. Как распорядиться свободными денежными средствами? Решение Сформулируем экономико-математическую модель задачи. Введем следующие обозначения: х1 – объем вложений в объект А; x2 – объем вложений в объект B; x3 – объем вложений в объект C; х4 – объем вложений в объект O. Прибыль от вложения в объект А составляет 1,06х1, в объект B составляет 1,08х2, в объект C составляет 1,1х3, в объект O составляет 1,09х4, т.е. необходимо максимизировать целевую функцию f(x) = 1,06 х1 +1,08 х2 +1,1 х3 +1,09 х4 -> max. Ограничения задачи имеют вид: 1,06 х1 +1,08 х2 +1,1 х3 +1,09 х4=100000 х1 + х250000 х3 25000 х4 20000 х1 30000 1. Обозначим через Х1,Х2, Х3, Х4количество вложений в каждый объект. В нашей задаче оптимальные значения вектора Х =( Х1,Х2, Х3, Х4)будут помещены в ячейках A2:B4, оптимальное значение целевой функции в ячейке E3. 2. Вводим исходные данные (рис.1) 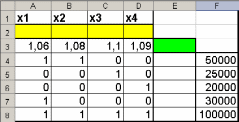 Рис.1 Исходные данные задачи 3. Введем зависимость для целевой функции • Курсор в ячейку «E3». • Курсор на кнопку «Мастер функций», расположенную на панели инструментов. • М1. На экране появляется диалоговое окно «Мастер функций шаг 1 из 2» • Курсор в окно «Категория» на категорию «Математические». • Курсор в окно «Функции» на «СУММПРОИЗВ».. На экране появляется диалоговое окно «СУММПРОИЗВ» (рис.2) 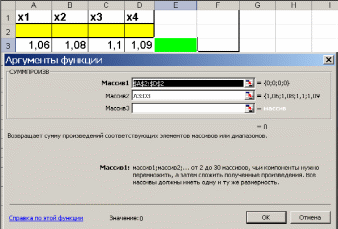 Рис.2 Диалоговое окно «СУММПРОИЗВ» • В строку «Массив 1» вводим А2:D2 • В строку «Массив 2» вводим А3:D3. Массив 1 будет использоваться при вводе зависимостей для ограничений, поэтому на этот массив надо сделать абсолютную ссылку. Введем зависимости для ограничений. • Курсор в ячейку «E3» (см. Рис.3). • На панели инструментов кнопка «Копировать в буфер». • Курсор в ячейку «E4». • На панели инструментов кнопка «Вставить из буфера». • Курсор в ячейку «E5». • На панели инструментов кнопка «Вставить из буфера». • Курсор в ячейку «E6». • На панели инструментов кнопка «Вставить из буфера». • Курсор в ячейку «E7». • На панели инструментов кнопка «Вставить из буфера». • Курсор в ячейку «E8». • На панели инструментов кнопка «Вставить из буфера». 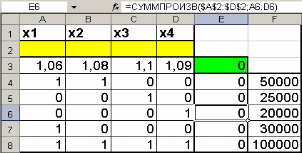 Рис.3 Ввод зависимостей для ограничений В строке «Меню» указатель мышки на имя «Сервис». В развернутом меню команда «Поиск решения». Появляется диалоговое окно «Поиск решения» (см. Рис.4). 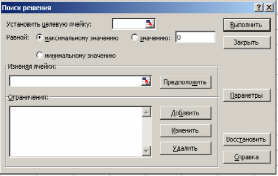 Рис.4 Диалоговое окно «Поиск решения» Назначаем целевую функцию (устанавливаем целевую ячейку), указываем адреса изменяемых ячеек. • Курсор в строку «Установить целевую ячейку». • Вводим адрес ячейки «$E$3». • Введем направление целевой «Максимальному значению». • Курсор в строку «Изменяя ячейки». • Вводим адреса искомых переменных А$2:D$2. 6. Введем ограничения • Указатель мышки на кнопку «Добавить. Появляется диалоговое окно«Добавление ограничения» • В строке «Ссылка на ячейку» вводим адрес $E$4. • Вводим знак ограничения . • В строке «Ограничение» вводим адрес $F$4 (рис. 9).. • Указатель мышки на кнопку «Добавить». На экране вновь диалоговое окно«Добавление ограничения». • Вводим остальные ограничения задачи, по выше описанному алгоритму • После введения последнего ограничения кнопка «ОК». На экране появляется диалоговое окно «Поиск решения» с введенными условиями (см. Рис.5). 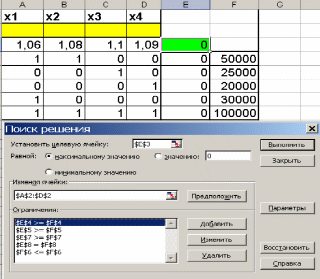 Рис.5 Диалоговое окно «Поиск решения» с введенными условиями 7. Введем параметры для решения ЗЛП. • В диалоговом окне указатель мышки на кнопку «Параметры». На экране появляется диалоговое окно «Параметры поиска решения» (Рис. 6). 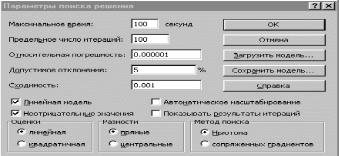 Рис.6 Диалоговое окно «Параметры поиска решения» • Устанавливаем флажки в окнах «Линейная модель» и «Неотрицательные значения». • Указатель мышки на кнопку «ОК». На экране диалоговое окно «Поиск решения». • Указатель мышки на кнопку «Выполнить». Появится диалоговое окно «Результаты поиска решения» (см. Рис.7) и исходная таблица с заполненными ячейками А3:D3 для значений Хi и ячейка E3 с максимальным значением целевой функции. 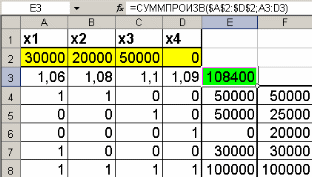 Рис.7 Диалоговое окно «Результаты поиска решения» В результате решения задачи получили ответ: Х1 = 30000 - необходимо вложить в объект А, Х2 = 20000 - необходимо вложить в объект B, Х3 = 50000 - необходимо вложить в объект C, Х4 = 0 - необходимо вложить в объект O, F(x) = 108400 чтобы получить максимальную прибыль. СПИСОК ЛИТЕРАТУРЫ Алексеева И.В. Сборник задач и упражнений по курсу «Информатика». – Обнинск: Обнинский институт атомной энергетики, 1996г. Брукшир Дж. Введение в компьютерные науки. Общий обзор, 6-е издание: Пер. с англ. — М.: Издательский дом «Вильямс», 2001г. Дюк В. Обработка данных на ПК в примерах. СПб: Питер. - 1997г. Денисов А.В, Вихарев И.П, Белов А.А. Самоучитель Интернет. – Спб: Питер, 2001г. - 461 с. Ежемесячный компьютерный журнал CompUnity № 9 за 1996 год. Журнал «Мир Internet» - 2004г - №№1-5. Информатика: Практикум по технологии работы на компьютере./ Под ред. Н.В. Макаровой. - М.: Финансы и статистика, 2000г. Косарев В.П. Компьютерные системы и сети, 2000г. Коцюбинский А.О., Грошев С.В. Современный самоучитель работы в сети Интернет. М.: Триумф, 1997г. Материалы журнала «BYTE/Россия» http://www.bytemag.ru/ Медведовский И.Д. Локальные и глобальные сети. - СПб: «Мир и семья-95», 1997г. Мизин И.А., Богатырев В.А.,Кулешов А.П. Сети, коммуникации пакетов/Под ред.В.С.Семенихина-М: Радиосвязь,1986г. Могилев А.В. и др. Информатика. – М., 1999г. – 816 с. Олифер В.Г., Олифер Н.А. Компьютерные сети (принципы, технологии, протоколы), 2005г. Основы современных компьютерных технологий: Учебное пособие/под. ред. Хомоненко. – СПб: КОРОНА, 1998г. Пайк М. Internet в подлиннике: Пер. с англ.-СПб.:BHV-Санкт-Петербург,1996г. Поспелов Д.А.. Информатика: Энциклопедический словарь для начинающих. – М.: Педагогика-Пресс, 1994г. – 352 с. Семьянов П.В. Глобальная сеть Интернет. - М.: Магистр, 2003г. Симонович С. В., Евсеев Г.А., Практическая информатика, Учебное пособие. М.: АСТпресс, 1999г Фролов А.В., Фролов Г.В. Глобальные сети компьютеров. Практическое введение в Internet, E-Mail, FTP, WWW и HTML. М.: Диалог-МИФИ, 1996г. Шафрин Ю.А. Основы компьютерной технологии. – М.: АБВ, 1997г. Экономическая информатика. – СПб.: Питер, 1997г. – 592 с. 24. Якубайтис Э.А. Информационные сети и системы: Справочная книга.- М.: Финансы и статистика, 1996г. |
