регрессия. ла. Год Квартал

• Название: Год Квартал
• Анкор: регрессия
• Дата: 21.10.2021
• Размер: 153.49 Kb.
• Имя файла: ла.docx
• Тип: Документы; #252654

Имеются данные об общем количестве правонарушений на таможне одного из субъектов РФ.

Таблица 1

Год	Квартал	t	Количество заказов, yt
2007	I	1	6329
	II	2	7180
	III	3	7762
	IV	4	9436
2008	I	5	10301
	II	6	10669
	III	7	11352
	IV	8	11259
2009	I	9	10916
	II	10	11010
	III	11	12772
	IV	12	15140
2010	I	13	16245
	II	14	17098
	III	15	16343
	IV	16	17238
2011	I	17	17668
	II	18	17320
	III	19	27510
	IV	20	25060

Данный временной ряд содержит сезонные колебания периодичностью 4, т.к. количество противонарушений в первый-второй кварталы ниже, чем в третий-четвертый.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

• 
  суммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени;
  
• 
  разделим полученные суммы на 4, найдем скользящие средние. Получаем таким образом выровненные значения, которые не содержат сезонной компоненты;
  
• 
  приведем эти значения в соответствие с фактическими моментами времени, для чего найдем среднее значение из двух последовательных скользящих средних – центрированные скользящие средние.
  

Таблица 2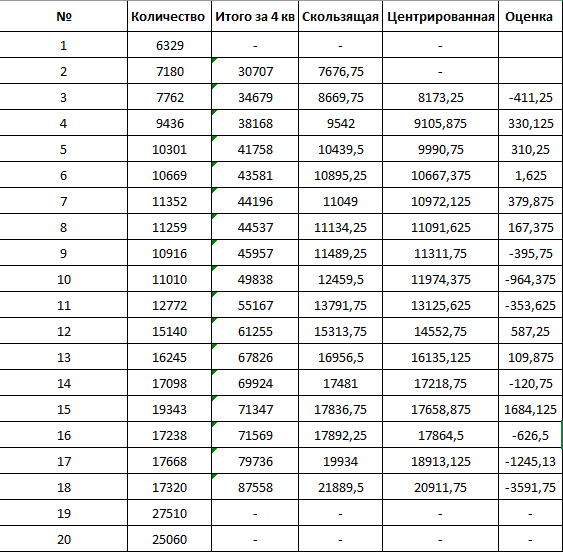



Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними, для расчета значений сезонной компоненты S. Найдем среднее за каждый квартал (по всем годам) оценки сезонной компоненты S_i. В моделях сезонной компоненты обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.

Таблица 3


Для данной модели имеем:

-305,188-1168,813+324,781+114,563= -1034,656

Корректирующий коэффициент:

k = -1034,656/4 = -258,664

Расчет скорректированных значений сезонной компоненты S_i = 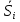– k

Проверка равенства нулю суммы значений сезонной компоненты:

-46,523-910,148+583,445+373,227= 0
Шаг 3. Исключим влияние сезонной компоненты путем вычитания ее из каждого уровня исходного временного ряда. Получим величины T + E = Y – S. Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.

Таблица 4
Решение с помощью ППП Excel

Для определения параметров линейного тренда по методу наименьших квадратов используется статистическая функция ЛИНЕЙН, для определения экспоненциального тренда – ЛГРФПРИБЛ. В качестве зависимой переменной в данном примере выступает время (t = 1, 2, …, n). Приведем результаты вычисления функции ЛИНЕЙН и ЛГРФПРИБЛ.

Результат вычисления функции ЛИНЕЙН

ЛИНЕЙН
891,6120301	4718,474
81,68333557	978,4968
0,868754437	2106,417
119,1474936	18
528656388,1	79865843

Результат вычисления функции ЛГРФПРИБЛ

ЛГРФПРИБЛ
1,066817	6628,308
0,004107	0,049197
0,932339	0,105906
248,0328	18
2,78196	0,20189

Далее построим диаграмму.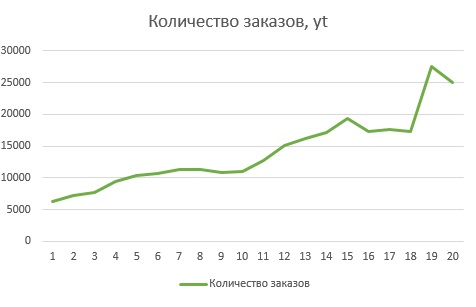



Рис. 3 – Динамика количества заказов

Нанесем на диаграмму линии тренда. В качестве дополнительной информации на диаграмме отобразим уравнение регрессии и значение среднеквадратического отклонения.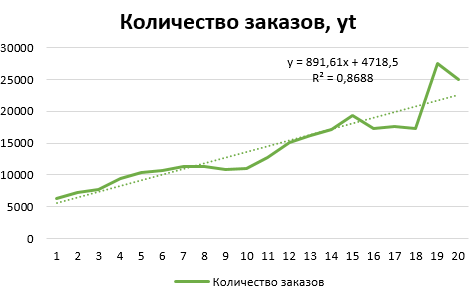



Рис. 4 - Линейный тренд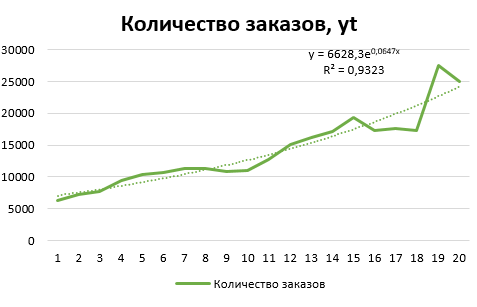



Рис. 5 - Экспоненциальный тренд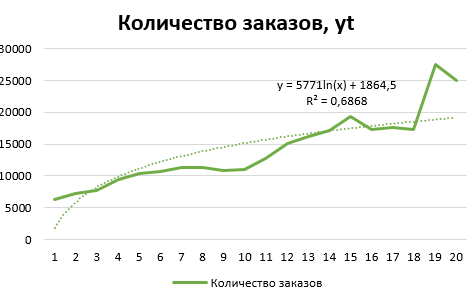



Рис. 6 - Логарифмический тренд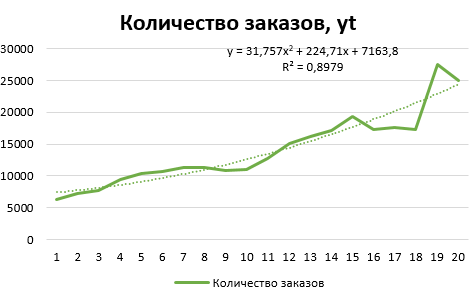



Рис. 7 - Полиномиальный тренд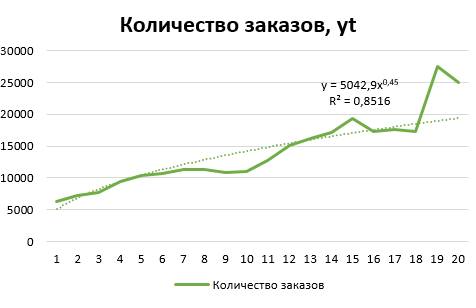



Рис. 8 - Степенной тренд

Сравним значения r_xy² (или R²) по разным уравнениям трендов:

• 
  линейный - r_xy² = 0,8688;
  
• 
  экспоненциальный - r_xy² = 0,9323;
  
• 
  логарифмический - r_xy² = 0,6868.
  
• 
  полиномиальный 2-й степени - r_xy² = 0,8979;
  
• 
  степенной - r_xy² = 0,8516;
  

ВЫВОД
Исходные данные лучше всего описывает экспоненциальный тренд. Следовательно, в рассматриваемом примере для прогнозных значений следует использовать экспоненциальное уравнение.