Государственного образовательного учреждения высшего профессионального образования
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
|
\ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ МУРОМСКИЙ ИНСТИТУТ (ФИЛИАЛ) Государственного образовательного учреждения высшего профессионального образования«ВЛАДИМИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» МЕТОДИЧЕСКИЕ УКАЗАНИЯ К выполнению контрольной работы по дисциплине «Устройства СВЧ и антенны» Факультет радиоэлектроники и компьютерных систем, кафедра Радиотехники 2014г. УДК 621.396.67 Федосеева Е.В. Устройства СВЧ и Антенны. Методические указания к контрольной работе Рассматриваются вопросы, связанные с разработкой СВЧ полосковых устройств. Предназначено для студентов специальности «Радиотехника». Федосеева Е.В., 2014 Порядок проведения расчетов полосковых СВЧ устройств и Задание №1 «Расчет микрополосковых устройств деления мощности СВЧ» 1 Общие сведения о полосковых линиях В интегральных СВЧ устройствах электрические цепи выполняются на основе несимметричных микрополосковых линий (МПЛ) и их модификаций. Конструктивно несимметричную микрополосковую линию (рисунок 1.1) выполняют в виде диэлектрической подложки с проницаемостью материала ε (3), на одной стороне которой нанесены проводники схемы (1) в виде пленки металла, а на другой - металлизированное покрытие, образующее проводящую заземляющую поверхность (2). 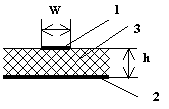 Рисунок 1.1 – Микрополосковая линия В несимметричной МПЛ распространяется волна квази-ТЕМ, при этом большая часть энергии поля сосредоточена в подложке под полоской, однако часть ее находится также в пространстве над подложкой и полоской, что эквивалентно уменьшению диэлектрической проницаемости среды в МПЛ по сравнению с величиной диэлектрической проницаемости подложки. 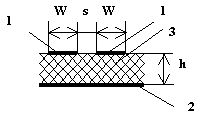 Рисунок 1.2 – Связные несимметричные МПЛ Кроме одиночных МПЛ в интегральных СВЧ устройствах, таких как фильтры и направленные ответвители, применяются связанные МПЛ. Связанные несимметричные МПЛ с боковой связью приведены на рисунок 1.2. 2 Разработка пассивных устройств СВЧ в полосковом варианте исполнения 2.1 Расчет полосковой линии Длина волны в МПЛ: где λ – длина волны в воздухе, мм где с – скорость света (3·108 м/с); f0 – центральная частота рабочего диапазона. Величина эффективной диэлектрической проницаемости среды в линии вычисляется по формуле: где h – толщина подложки; ω – ширина полоски, мм; ε - диэлектрическая проницаемость. Ширина проводящей полоски определяется, используя ее зависимость от волнового сопротивления микрополоской линии (рисунок 2.1): 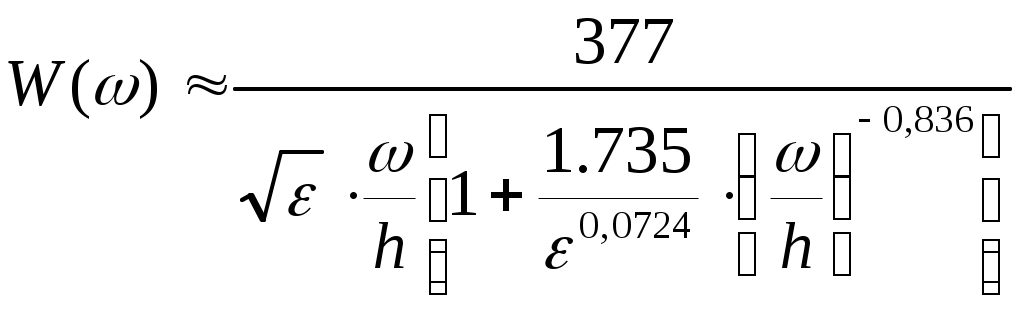 . (2.1.4) . (2.1.4)При расчетах можно воспользоваться приближенной формулой: откуда требуемое отношение ω/h для получения заданной величины волнового сопротивления равно: Отличие результата расчета W по формуле (2.1.5) от данных рисунка 2.1 и формулы (2.4) достигает 5-10 % [1]. Если любой из размеров МПЛ (h или ω) приближается к Λ/4, в линии наряду с ТЕМ-волной могут возникнуть поверхностные ТМ и ТЕ-волны, в результате чего параметры МПЛ изменятся. Рабочая частота МПЛ должна быть ниже критической частоты поверхностной ТЕ-волны наинизшего типа, определяемой соотношением: 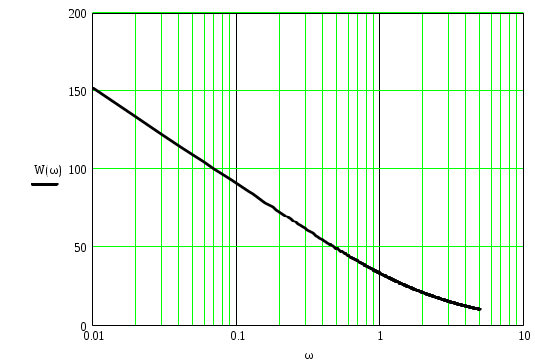 Рисунок 2.1 – Зависимость волнового сопротивления микрополосковой линии от ширины проводящей полоски ω Исходя из этого, видно, что значение частоты заданное в техническом задании полностью удовлетворяет условию распространения в линии только ТЕМ-волны. Потери мощности в МПЛ α: где αп - потери проводимости; αд – диэлектрические потери. Погонные (на единицу длины) потери проводимости приближенно оценивают по формуле: где Rп – поверхностное сопротивление проводников МПЛ, представляющее собой сопротивление части поверхностного слоя (скин-слоя) пленочного проводника толщиной δс в форме квадрата: где σ – удельная проводимость проводника; ω = 2πf – рабочая частота, с-1; μ0 = 1,256·10-6 Гн/м – магнитная проницаемость вакуума; μ – относительная магнитная проницаемость проводника. Погонные диэлектрические потери в подложке МПЛ рассчитываются по формуле: где δ – угол потерь диэлектрика подложки. Размеры МПЛ выбирают, учитывая следующие соображения. Большая часть энергии поля МПЛ сосредоточена в области поперечного сечения линии шириной ω + 2h, т.е. в пространстве непосредственно под полосковым проводником и по обе стороны от него протяженностью h с каждой стороны. Поэтому ширина основания МПЛ (ширина заземленной поверхности подложки) должна быть больше ω + 2h. От сюда следует также, что минимальное расстояние между двумя полосковыми проводниками, которые не должны иметь заметной взаимной связи, следует выбирать большим удвоенной толщины подложки: МПЛ нуждается в экранировке. Обычно СВЧ ИС для экранировки, а также для защиты от механических повреждений помещают в металлический корпус. Расстояние от его стенок до поверхности подложки с полосовыми проводниками должно в 4-5 раз больше толщины подложки: 2.2 Разработка делителей мощности В идеальном мосте при подаче СВЧ колебаний в одно из его плеч мощность колебаний распределяется поровну между определенной парой двух других плеч, а в четвертое плечо, называемое изолированным, мощность не поступает (предполагается, что все плечи остаются нагружены на согласованные нагрузки). Необходимо подчеркнуть, что пара плеч, между которыми распределяется мощность, тоже обладает взаимной развязкой. Номинальный сдвиг фаз колебаний Θ0 = Θ3 - Θ4 зависит от типа моста. Реальные СВЧ мосты характеризуются рядом параметров. Из-за неидеальности свойств реальных мостов мощность входного сигнала распределяется между выходными плечами не строго равномерно, а сдвиг фаз колебаний в них несколько отличается от номинального Θ0. Наибольшее распространение в СВЧ ИС получили квадратные (или шлейфные) и кольцевые мосты. Квадратный мост представляет собой четырехплечное устройство, в котором два параллельных отрезка МПЛ параллельно соединены между собой несколькими шлейфами (минимум двумя), имеющими длину и интервал между ними равными четверти длины волны в линии Λ0/4 на средней частоте рабочего диапазона волн (рисунок 2.2). Квадратный мост является квадратурным, т.е. сдвиг фаз колебаний в выходных плечах Θ0 = π/2. Как видно из рисунка 2.2, он полностью симметричен, поэтому его свойства одинаковы со стороны любого плеча. Мощность, поданная, например, в плечо 1, распределяется поровну между плечами 3, 4 и не поступает в плечо 2 из-за противофазности возникающих в нем СВЧ колебаний. 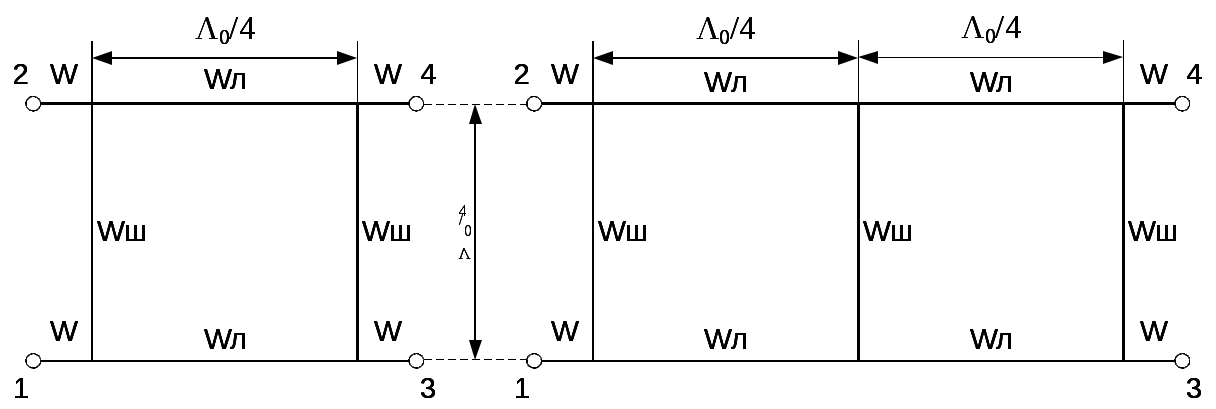 Рисунок 2.2 – Эквивалентная схема двух- и трехшлейфного квадратного моста Отражения мощности во входном плече 1 при этом не происходит, т.к. КСВ этого плеча ρ1 = 1. Для получения таких свойств моста волновые сопротивления составляющих отрезков основных линий (Wл) и шлейфов (Wш) должны находиться в определенном соотношении с волновым сопротивлением подводящих линий (W). Кольцевой мост представляет собой сочленение четырех параллельных Т-тройников, боковые плечи которых соединены последовательно и образуют замкнутое кольцо (рисунок 2.3). Длина средней окружности кольца обычно равна 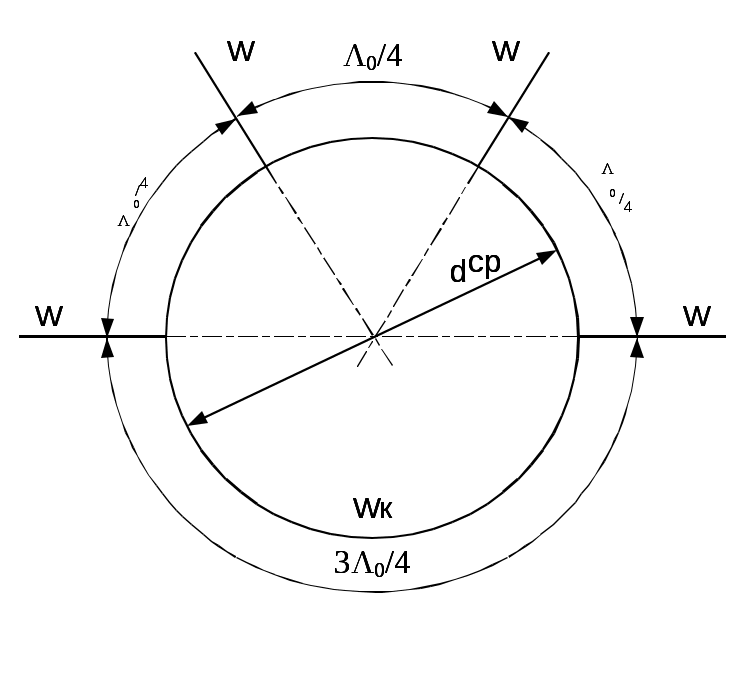 Рисунок 2.3 – Эквивалентная схема кольцевого моста Направленные ответвители мощности на связанных линиях представляют собой две связанные линии (восьмиполюсник), одна из которых – основная – включается в МПЛ, откуда ответвляется часть мощности, другая – побочная – эту мощность отводит в требуемую часть устройства. 2.2.1 Разработка двухшлейфного моста На рисунке 2.4 изображена топологическая схема полоскового проводника двухшлейфного квадратного моста, на которой приведены основные размеры и отношение величин волнового сопротивления отрезков основных линий и шлейфов к волновому сопротивлению подводящей линии. Волновое сопротивление основной линии: где W – волновое сопротивление подводящих линий Волновое сопротивление шлейфов: Ширина шлейфа и полоски основной линии вычисляется, используя формулу (2.1.6). 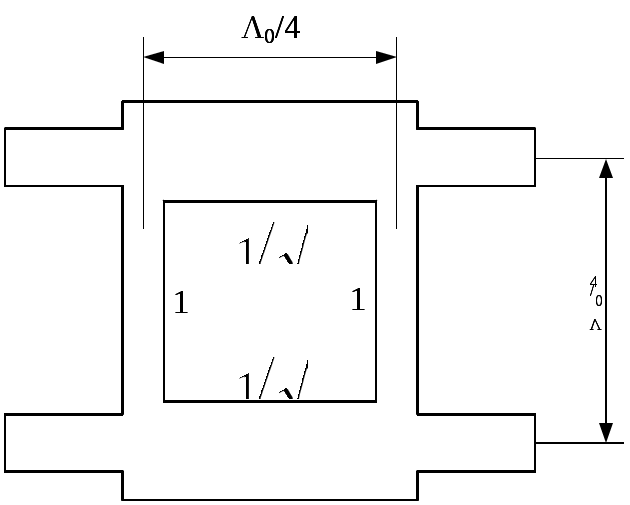 Рисунок 2.4 - Топологическая схема полоскового проводника двухшлейфного квадратного моста Размеры четвертьволновых отрезков шлейфов и основной линии моста вычисляются с использованием формул (2.1.1) и (2.1.3). 2.1.2 Разработка трехшлейфного моста На рисунке 2.5 изображена топологическая схема полоскового проводника трехшлейфного квадратного моста, на которой приведены основные размеры и отношение величин волнового сопротивления отрезков основных линий и шлейфов к волновому сопротивлению подводящей линии. Волновое сопротивление основной линии: где W – волновое сопротивление подводящих линий 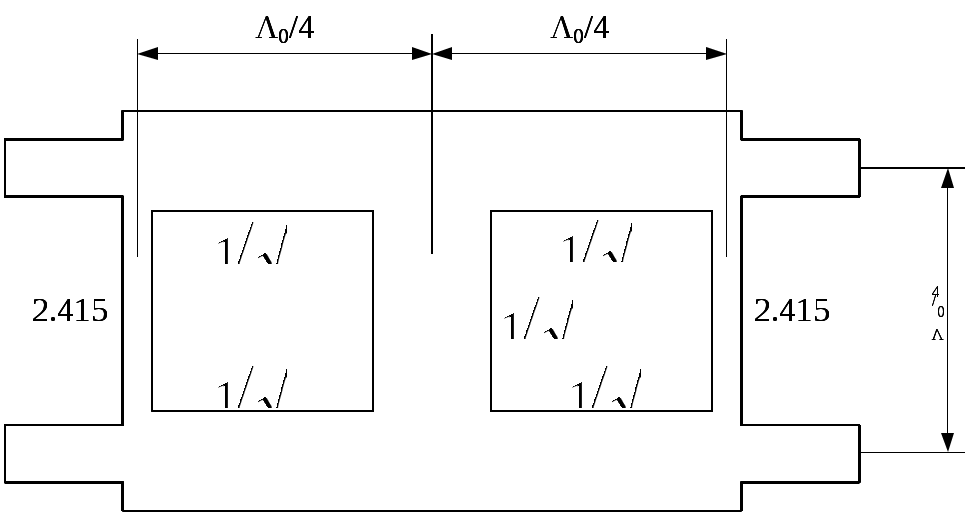 Рисунок 2.5 – Топологическая схема полоскового проводника Волновое сопротивление крайних шлейфов: Волновое сопротивление среднего шлейфа: Ширина полоска основной линии и среднего шлейфа моста вычисляется по формуле (2.1.6) Размеры четвертьволновых отрезков крайних шлейфов и основной линии моста вычисляются с использованием формул (2.1.1) и (2.1.3). 2.1.3 Разработка кольцевого моста На рисунке 2.6 изображена топологическая схема полоскового проводника кольцевого моста, на которой приведены основные размеры. Волновое сопротивление кольцевой линии: 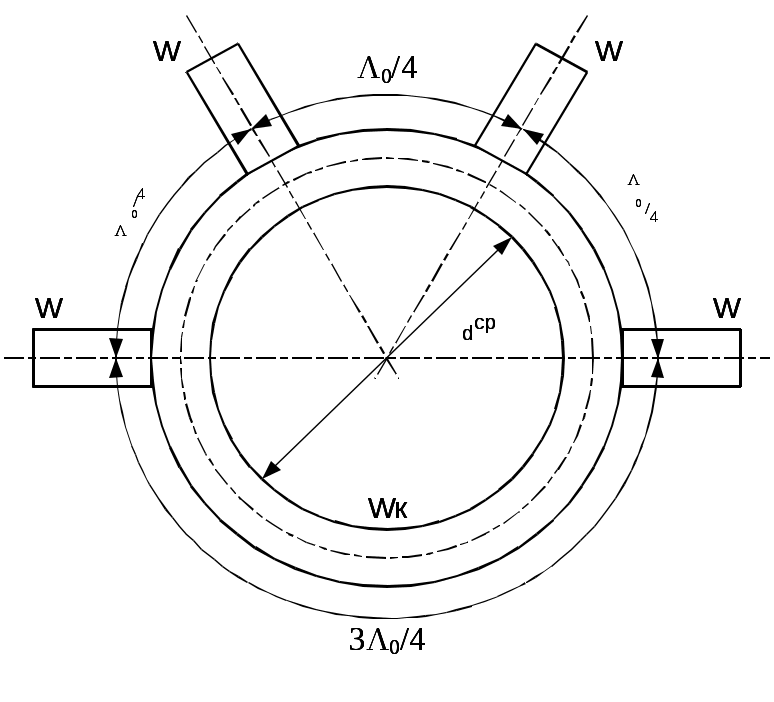 Рисунок 2.6 – Топологическая схема кольцевого делителя мощности Из рисунка 2.1 или по формуле (2.1.6) находим ширину МПЛ. По формуле (2.1.1) и (2.1.3) вычисляем длину волны в кольцевой линии. Длина средней окружности кольца: Диаметр средней окружности кольца: Расстояние между ближайшими плечами моста: 2.1.4 Разработка направленного ответвителя на связанных линиях. На рисунке 2.7 изображена топологическая схема полоскового проводника направленного ответвителя на связанных линиях, на которой приведены основные размеры. Амплитудный коэффициент связи: 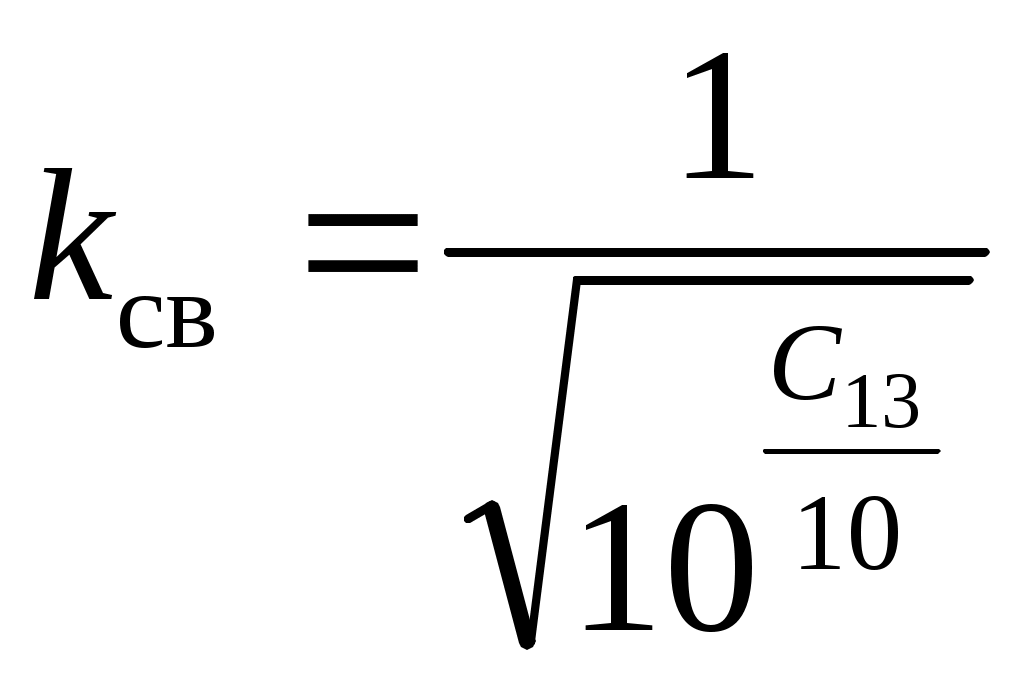 ; (2.2.10) ; (2.2.10)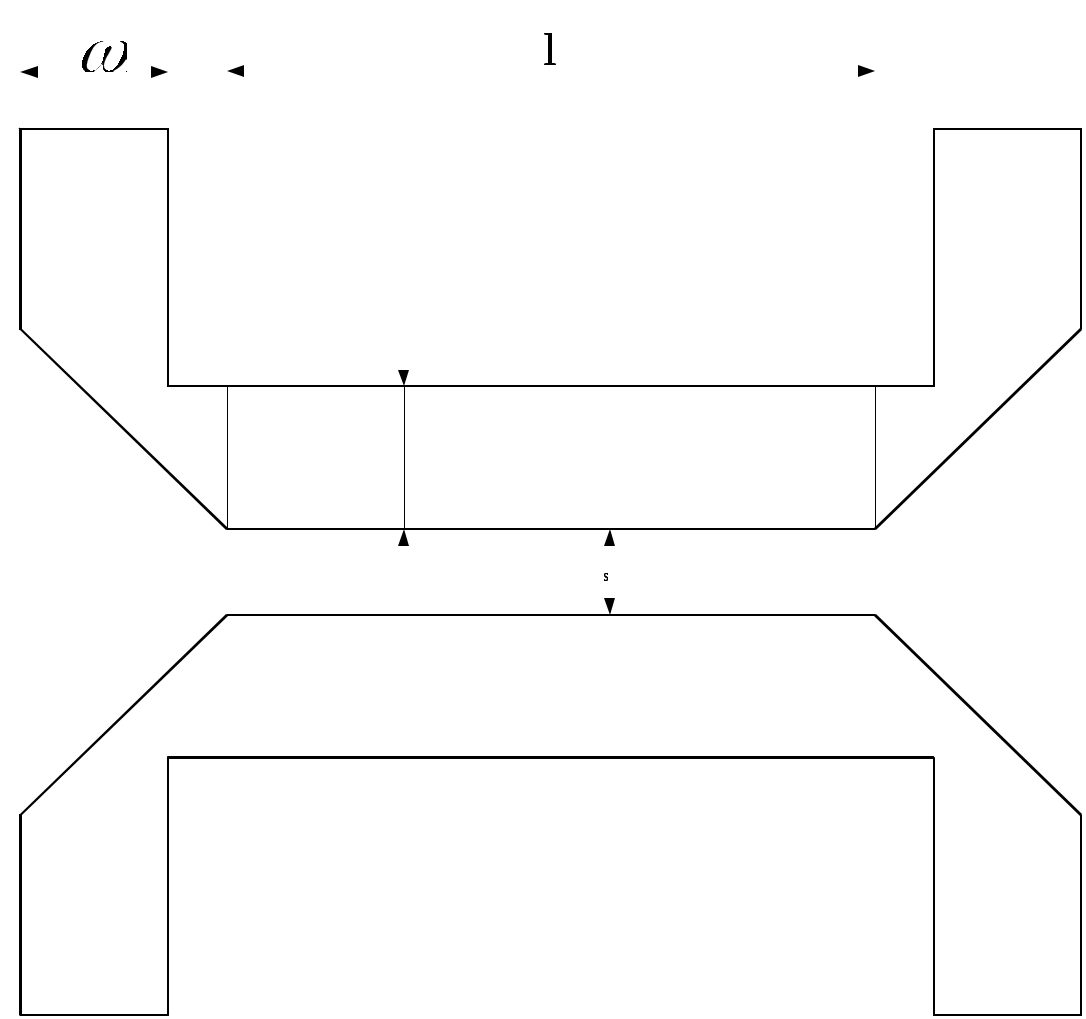 Рисунок 2.7 – Топологическая схема направленного ответвителя на связанных линиях Характеристические сопротивления четного Wое и нечетного Wоо типов колебаний: Используя полученные значения Длина области связи: 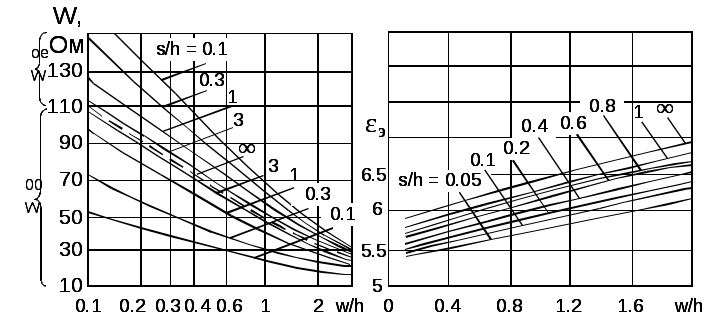 Рисунок 2.8 – Зависимость параметров параллельно связанных микрополосковых линий от размеров МПЛ (ω/h) и нормированной ширины зазора (s/h) между полосками (ε = 9,8) 3 Пример расчета трехшлейфного моста Исходные данные: f0 = 9,375 ГГц; ε = 9,8; h = 0,5 мм; W = 50 Ом. На рисунке 2.5 изображена топологическая схема полоскового проводника трехшлейфного квадратного моста, на которой приведены основные размеры и отношение величин волнового сопротивления отрезков основных линий и шлейфов к волновому сопротивлению подводящей линии. Волновое сопротивление основной линии определяется по формуле (2.2.3): Волновое сопротивление крайних шлейфов определяется по формуле (2.2.4): Волновое сопротивление среднего шлейфа определяется по формуле (2.2.5): Из рисунка 2.1 видно, что для заданных величин ε и h подложки и при минимальной ширине полоскового проводника ω = 0.1 мм, еще допустимой с точки зрения потерь проводимости МПЛ и практической возможности качественного изготовления линии, волновое сопротивление МПЛ будет равно 90 Ом, что меньше требуемой величины 121 Ом. Следовательно, необходимо снизить волновое сопротивление подводящих линий. Для этого между исходной подводящей линией с W = 50 Ом и основной линией моста следует включить трансформирующий четвертьволновой отрезок МПЛ (рисунок 3.1), волновое сопротивление которого определим из условия практической реализуемости крайних шлейфов моста. С учетом сказанного зададим для последних ширину полоски ω = 0,1 мм (ω/h = 0.2) и по формуле (2.1.4) найдем: 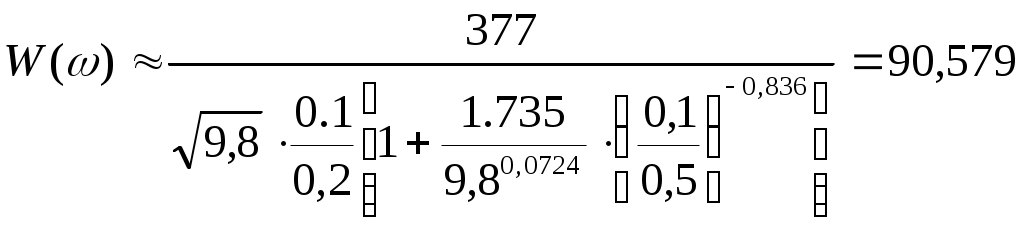 Ом. Ом.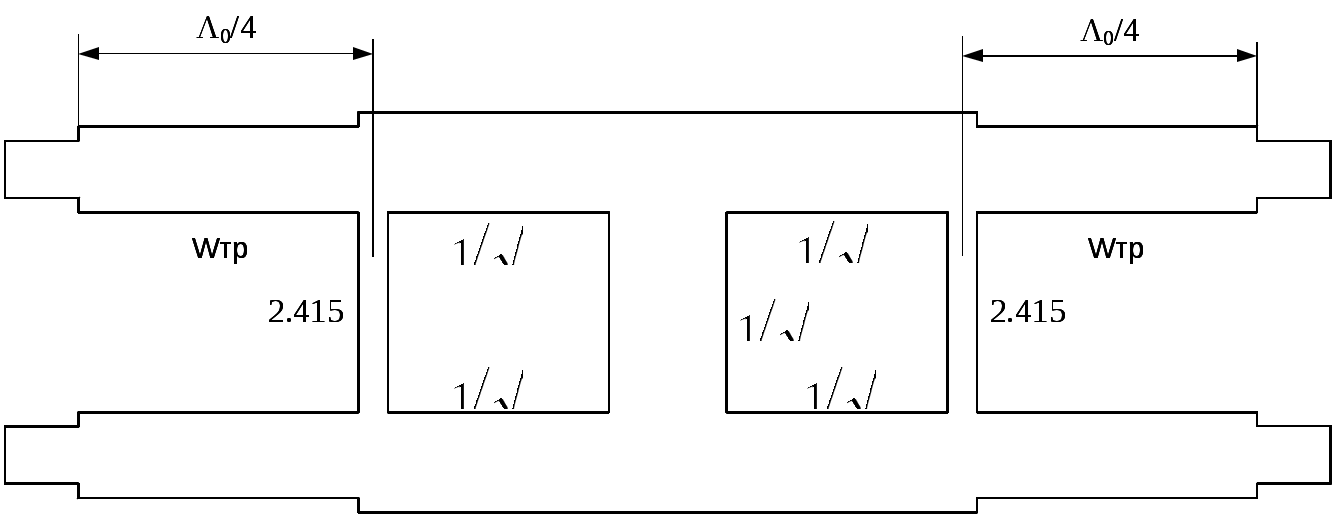 Рисунок 3.1 - Трехшлейфный квадратный мост с трансформирующими четвертьволновыми отрезками МПЛ в подводящих линиях Из соотношения (2.2.4) определим требуемое значение волнового сопротивления подводящих линий: Волновое сопротивление трансформирующего отрезка линии: Отношение размеров трансформирующего отрезка МПЛ найдем по формуле (2.1.5): Отсюда Волновое сопротивление основной линии и среднего шлейфа моста: Ширина полоска основной линии и среднего шлейфа моста: Размеры четвертьволновых отрезков основной линии моста: Размеры четвертьволновых отрезков крайних шлейфов моста: 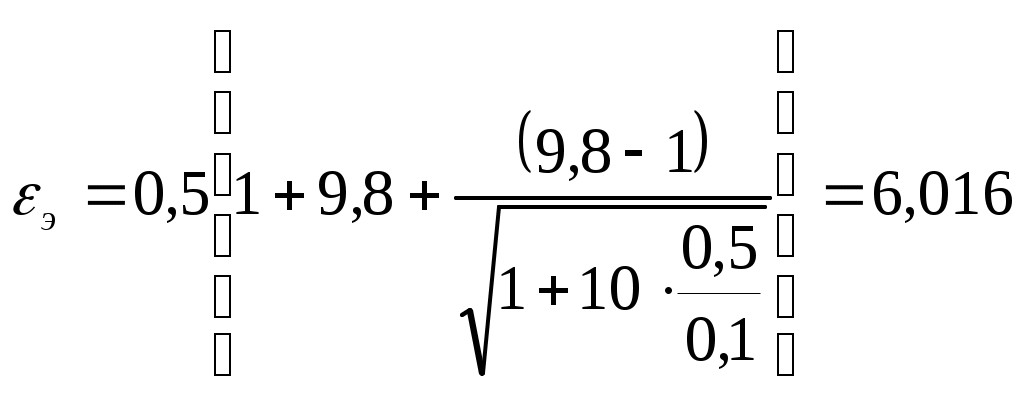 ; ;Размеры четвертьволновых трансформирующих отрезков моста: Задание №2 Расчет микрополосковых фильтров СВЧ 1 Общие сведения о фильтрах СВЧ Фильтрами СВЧ называют пассивные четырехполюсники, осуществляющие передачу СВЧ-колебаний в согласованную нагрузку в соответствии сзаранее заданной частотной характеристикой. По взаимному расположению полос пропускания и заграждения принято выделять следующие типы фильтров: фильтры нижних частот (ФНЧ), пропускающие сигналы с частотами ниже граничной частоты и подавляющие сигналы с частотами выше граничной; фильтры верхних частот (ФВЧ), пропускающие сигналы на частотах выше заданной и подавляющие сигналы на частотах других частот; полосно-пропускающие фильтры (ППФ), пропускающие в пределах заданной полосы частот и подавляющие сигналы вне этой полосы; полосно-запирающие фильтры (ПЗФ), подавляющие сигналы в пределах заданной полосы частот и пропускающие сигналы вне этой полосы. Частотная характеристика каждого фильтра имеет переходную область между полосой пропускания и полосой заграждения. В этой области затухание меняется от максимального значения до минимального. Обычно стараются уменьшать эту область, что приводит к усложнению фильтра, увеличению числа его звеньев. При проектировании фильтров, как правило, задаются следующие характеристики: полоса пропускания, полоса заграждения, средняя частота, затухание в полосе пропускания, затухание в полосе заграждения. Фильтры СВЧ на полосковых и микрополосковых линиях строят как на коротких отрезках, так и на резонансных отрезках линий. Как известно, МПЛ в отличие от полых волноводов не имеют нижней частоты отсечки, а потому на их основе могут быть реализованы практически все типы фильтров, включая фильтры нижних частот. Возможность создания фильтров на отрезках линий, играющих роль реактивных элементов, основана на том, что короткозамкнутые и разомкнутые отрезки линий длиной l < Λ0/4 эквивалентны соответственно индуктивности и емкости, а при длинах l = Λ0/4 или Λ0/2 они становятся резонансными и эквивалентны параллельному или последовательному колебательному контуру (в зависимости от длины и того, замкнуты или разомкнуты они на конце). Для аппроксимации частотных характеристик затухания применяется ряд функций, удовлетворяющих условиям физической реализуемости фильтров. Наиболее широко используемыми функциями аппроксимации частотных характеристик фильтров являются полиномы Чебышева и максимально плоские функции Баттерворта. Чебышевская характеристика имеет более крутые склоны по сравнению с максимально плоской (меньшую величину полосы перехода), но зато пульсирующий характер затухания и коэффициента стоячей волны в полосе пропускания. Для получения чебышевской характеристики требуется меньшее число звеньев фильтра, чем для получения максимально плоской. Переходы с максимально-плоской частотной характеристикой не имеют осцилляций в полосе пропускания; их фазо-частотная характеристика близка к линейной. 2 Разработка фильтров СВЧ 2.1 Разработка фильтра нижних частот Для расчета ФНЧ СВЧ диапазона обычно используют метод сравнения с фильтрами-прототипами нижних частот из элементов с сосредоточенными параметрами (рисунок 2.1). 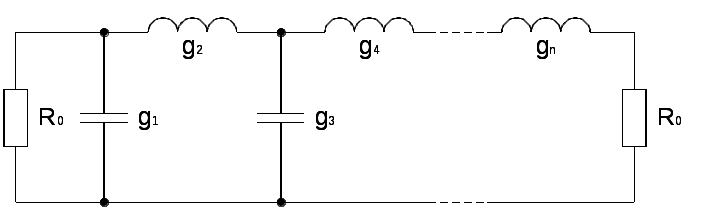 Рисунок 2.1 – Эквивалентная схема нормированного фильтра-прототипа нижних частот. Число резонаторов фильтра с чебышевской характеристикой затухания: где Lз и Lп – затухания в полосе пропускания и заграждения (в безразмерных еденицах). Полученный результат округляется до ближайшего целого. Обобщенные параметры прототипной схемы ФНЧ: 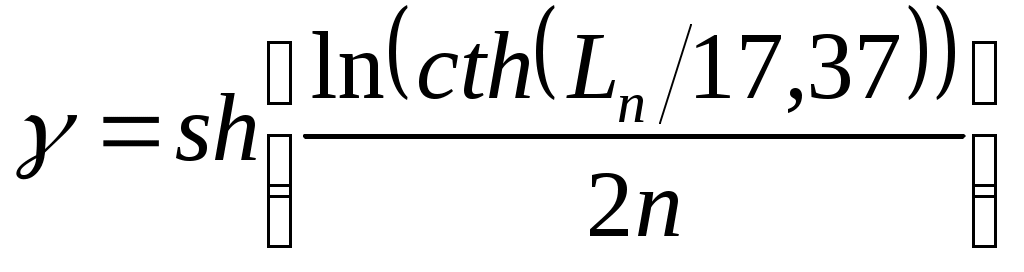 ; (2.3) ; (2.3)где i = 1, 2, …,n; Сущность реализации полоскового фильтра СВЧ состоит в том, что сосредоточенные элементы лестничной схемы фильтра-прототипа (рисунок 2.1) приближенно заменяют отрезками несимметричного полоскового волновода. В данном случае, ФНЧ образован чередованием последовательно включенных коротких отрезков линий с большим WLi и малым WCi волновыми сопротивлениями, эквивалентных соответственно индуктивности (из-за большой погонной индуктивности и малой погонной емкости) и емкости (из-за большой погонной емкости и малой погонной индуктивности). Токонесущая полоска СВЧ фильтра нижних частот изображена на рисунке 2.2. 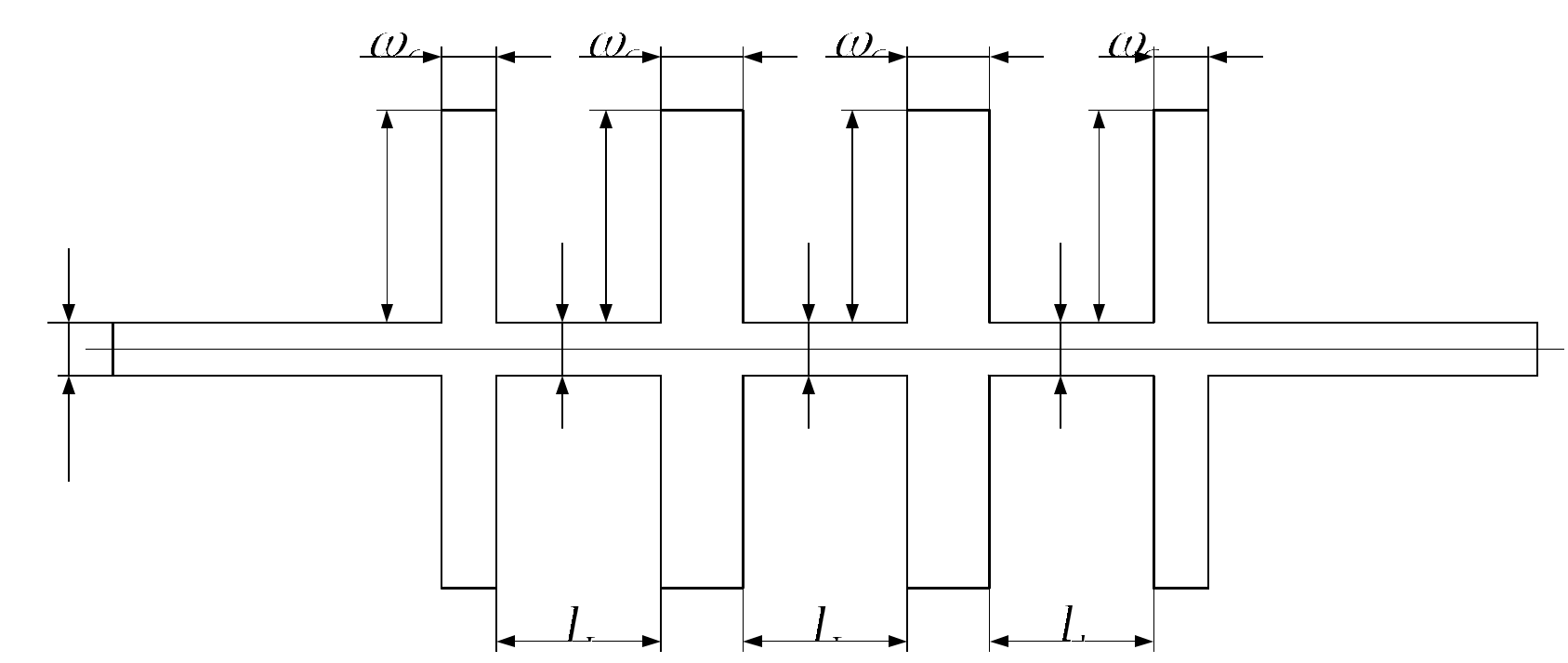 Рисунок 2.2 – Топологическая схема микрополоскового ФНЧ Характеристические сопротивления разомкнутых отрезков, аппроксимирующих емкости фильтра-прототипа: где W – волновое сопротивление подводящей линии (50 Ом). Характеристические сопротивления короткозамкнутых отрезков, аппроксимирующих индуктивности фильтра-прототипа: Как показывают эксперименты, при такой аппроксимации краевую емкость разомкнутого конца полоскового волновода учитывать не следует. Поэтому берется длина волновода: где Λ – длина волны в полосковом волноводе с диэлектриком, соответствующая частоте среза фильтра. 2.2 Разработка полосно-пропускающего фильтра Для проектирования полосно-пропускающих фильтров (ППФ) также используют фильтры прототипы (рисунок 2.3). Таким образом, ППФ состоит из каскадно-включенных резонаторов, которые реализуются в виде короткозамкнутых или разомкнуты отрезков линии передачи. 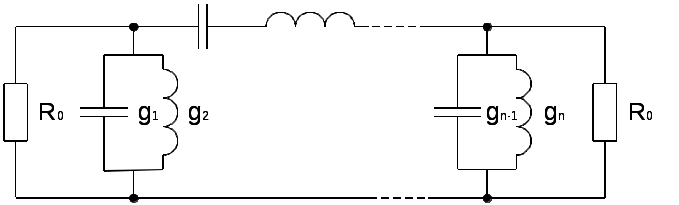 Рисунок 2.3 – Эквивалентная схема ППФ Полосно-пропускающий фильтр на одинаковых связанных линиях представляет собой каскадное включение четвертьволновых связанных линий передачи, два плеча которых соединяются с соседними каскадами, а два других работают в режиме холостого хода или короткого замыкания (рисунок 2.4). Число элементов прототипной схемы ФНЧ определяется по формуле: Полученный результат округляется до ближайшего целого. 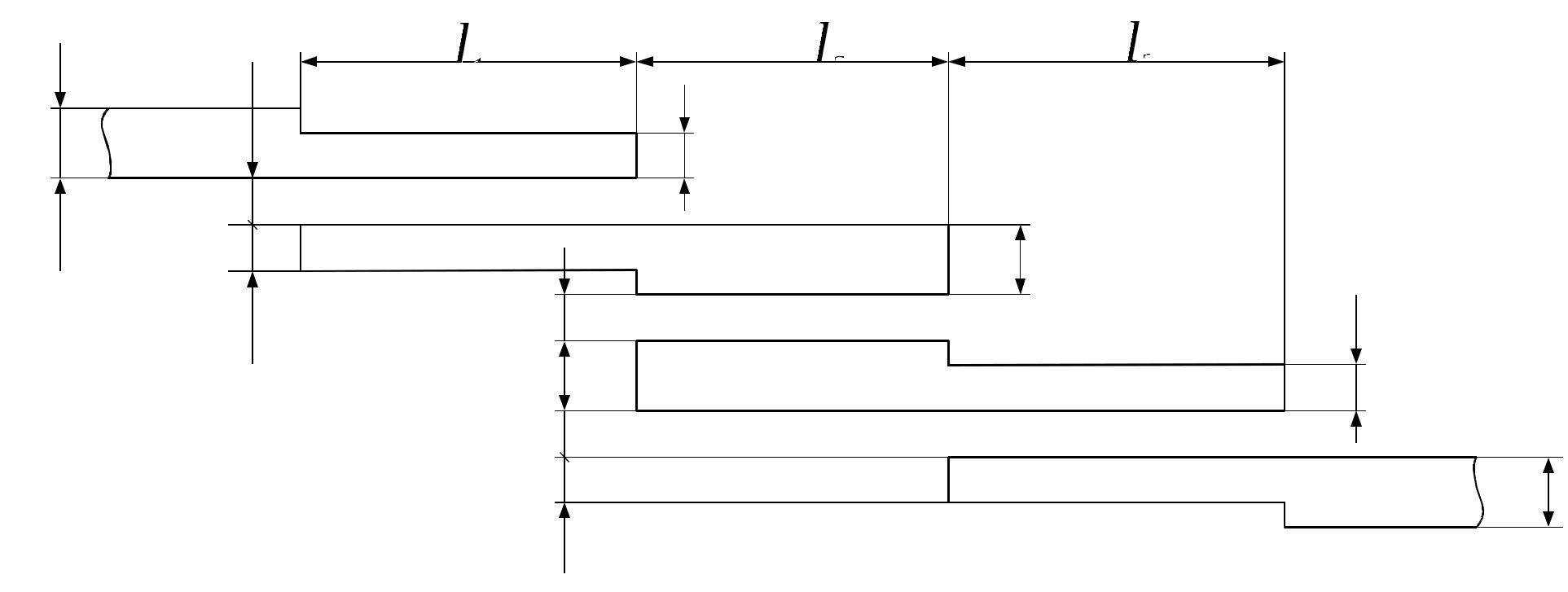 Рисунок 2.4 – Топологическая схема микрополоскового ППФ на одинаковых связанных линиях. Число связанных четверть волновых звеньев фильтра n + 1. Волновые сопротивления связанных линий i-го звена фильтра при четном где где W0 – заданное волновое сопротивление подводящих линий на входе и выходе фильтра; gi-1, gi – обобщенные параметры прототипной схемы ФНЧ. где коэффициент r при четном числе элементов n чебышевского прототипного ФНЧ: Используя полученные значения  Рисунок 2.5 – Зависимость параметров параллельно связанных микрополосковых линий от размеров МПЛ (ω/h) и нормированной ширины зазора (s/h) между полосками (ε = 9,8) По кривым рисунка 2.5 находим эффективную диэлектрическую проницаемость МПЛ каждого звена εэ(i) и с ее помощью соответствующие длины четвертьволновых отрезков связанных линий: Из-за неоднородности, которую представляет собой разомкнутый конец линии, на нем накапливается избыточный электрический заряд, что эквивалентно появлению концевой сосредоточенной емкости, включенной параллельно МПЛ. Кроме того, с этого конца возникает излучение, что увеличивает потери в линии. Сосредоточенная концевая емкость увеличивает эффективную длину линии по сравнению с физической на величину Δl, зависящую от размеров (рисунок 2.6). Поэтому требуемые длины отрезков МПЛ каждого звена равны: 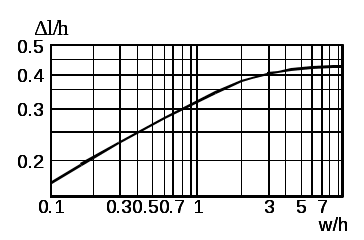 Рисунок 2.6 – Зависимость величины уменьшения разомкнутого отрезка МПЛ от его размеров 2.3 Разработка полосно-заграждающего фильтра Полосно-заграждающие фильтры реализуются в виде линии передачи с разомкнутыми шлейфами. Число шлейфных ответвлений равно числу элементов прототипного фильтра нижних частот (рисунок 2.7). 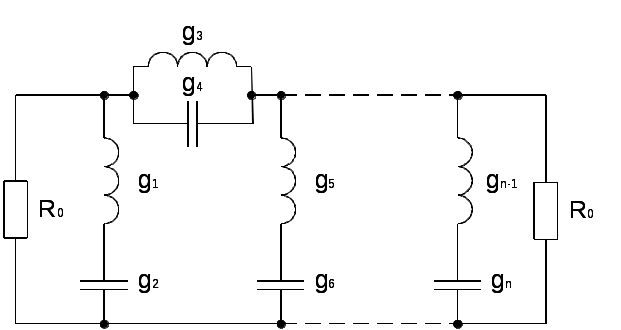 Рисунок 2.7 – Эквивалентная схема ПЗФ Число элементов прототипной схемы ФНЧ: где α – вспомогательный параметр, На рисунке 2.8 изображена топологическая схема полоскового полосно-заграждающего фильтра, на которой приведены основные размеры. Обобщенные параметры прототипной схемы ФНЧ: 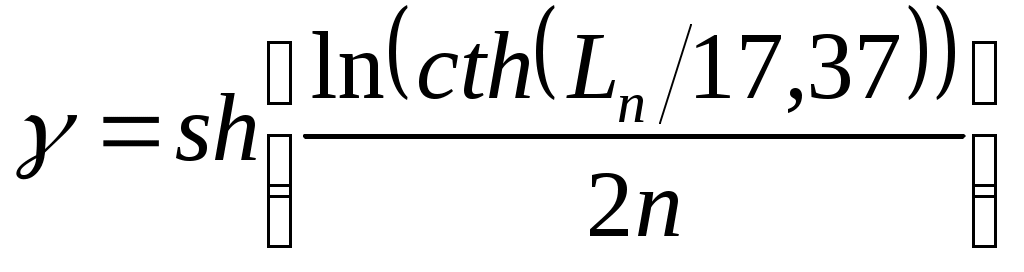 ; (2.23) ; (2.23)где i = 1, 2, …, n; 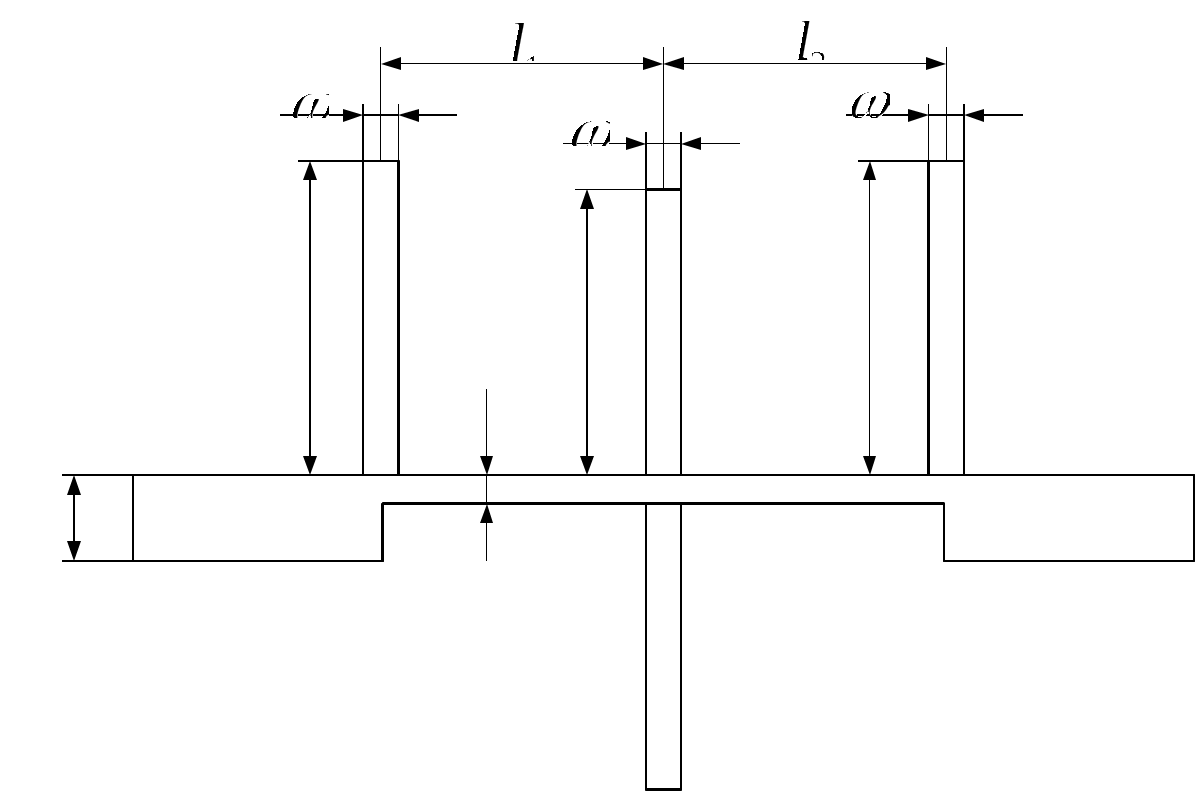 Рисунок 2.8 – Топологическая схема микрополоскового полосно-заграждающего фильтра Волновые сопротивления отрезков соединительных линий и шлейфов: Длины соединительных и шлейфных отрезков линии передачи: 2.4 Разработка фильтра верхних частот Для расчета фильтров верхних частот диапазона СВЧ также используются фильтры-прототипы (рисунок 2.9). Схема ФВЧ может быть получена непосредственно, если синтезирован ФНЧ с такой же частотой среза. Для этого в теории цепей используется прием, называемый преобразованием частоты. Каждый конденсатор с емкостью С ФНЧ должен быть заменен на катушку с индуктивностью: где ωс – частота среза, с-1. 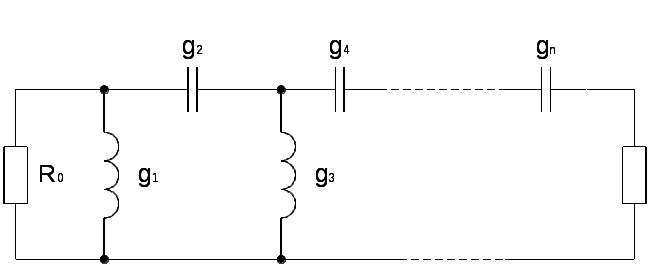 Рисунок 2.9 – Эквивалентная схема ФВЧ Аналогично катушка с индуктивностью L в низкочастотном фильтре должна быть заменена на конденсатор с емкостью: Резистивные элементы фильтра остаются без изменения. Для того чтобы пересчитать значения элементов ФНЧ необходимо сначала рассчитать значения элементов ФНЧ. При этом емкость ФНЧ рассчитывается по формуле: Индуктивности ФНЧ: По формулам (2.31) и (2.32) определяем индуктивности и емкости ФВЧ. Таким образом, ФВЧ можно выполнить, соединяя параллельные индуктивности в виде короткозамкнутых отрезков МПЛ с большим волновым сопротивлением, имеющим малую длину (не превышающую Λ/8) и последовательные емкости (рисунок 2.10). 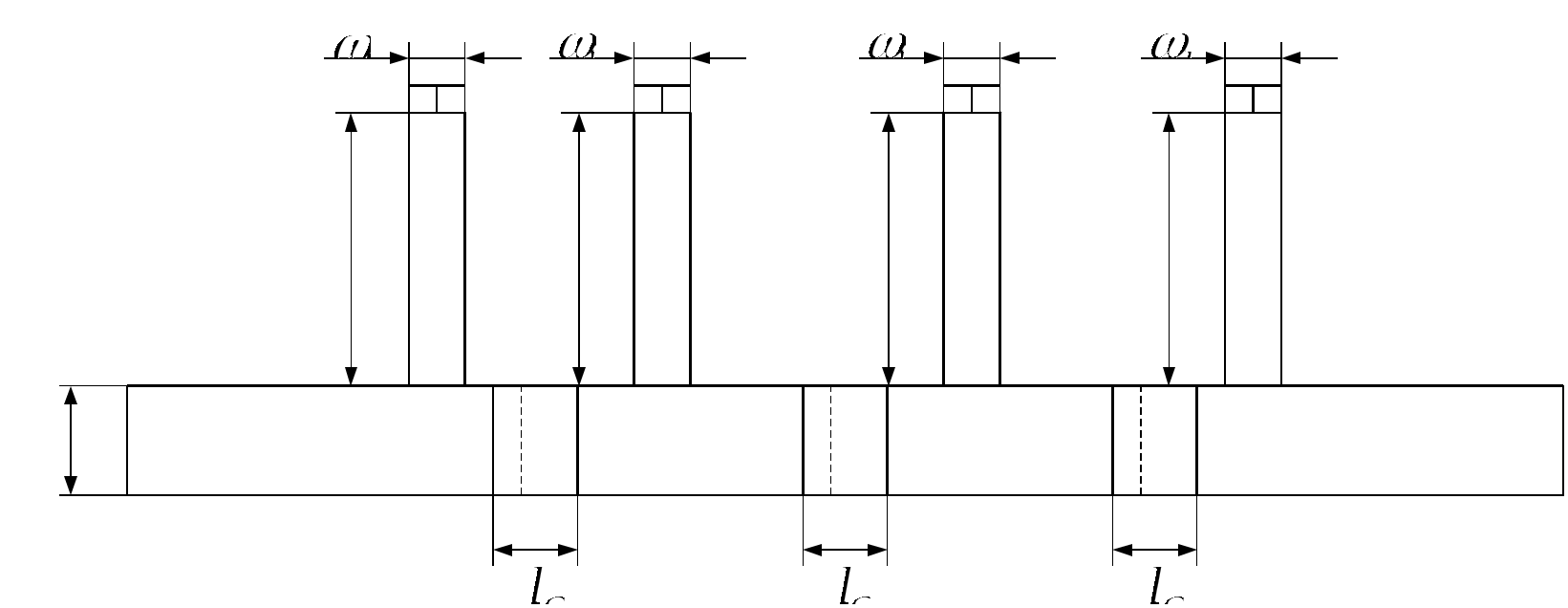 Рисунок 2.10 - Топологическая схема микрополоскового фильтра верхних частот Короткозамкнутый шлейф с высоким волновым сопротивлением представляет собой параллельную индуктивность. Его длина (мм) равна: где WLi – волновое сопротивление шлейфа выбираем 72,3 Ом при ωi = 0,2 мм. Результаты вычислений занесли в таблицу 2.6. Последовательная емкость может быть реализована как трехслойная конструкция (рисунок 2.11). 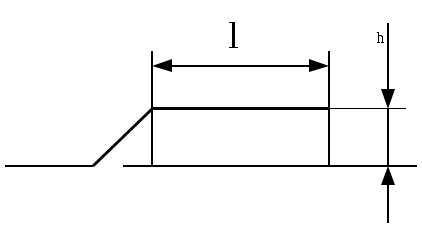 Рисунок 2.11 – Трехслойный вариант реализации сосредоточенной последовательной емкости 3 Пример расчета ФНЧ Исходные данные: fc = 9,375 ГГц; Lп = 0,5 дБ (чебышевская характеристика); fз = 12,2 ГГц; Lз = 30 дБ; волновое сопротивление подводящих линий W = 50 Ом; ε=9,8; h=0,5 мм. По формуле 2.1 определяем число резонаторов фильтра с чебышевской характеристикой затухания: Полученный результат округляется до ближайшего целого n = 7. Обобщенные параметры прототипной схемы ФНЧ рассчитываются по формулам: 2.2 – 2.6. Результаты расчета сведены в таблицу 2.1 Таблица 2.1
Сущность реализации полоскового фильтра СВЧ состоит в том, что сосредоточенные элементы лестничной схемы фильтра-прототипа (рисунок 2.1) приближенно заменяют отрезками несимметричного полоскового волновода. В данном случае, ФНЧ образован чередованием последовательно включенных коротких отрезков линий с большим WLi и малым WCi волновыми сопротивлениями, эквивалентных соответственно индуктивности (из-за большой погонной индуктивности и малой погонной емкости) и емкости (из-за большой погонной емкости и малой погонной индуктивности). Токонесущая полоска СВЧ фильтра нижних частот изображена на рисунке 2.2. Характеристические сопротивления разомкнутых отрезков, аппроксимирующих емкости фильтра-прототипа вычисляются по формуле 2.7. Характеристические сопротивления короткозамкнутых отрезков, аппроксимирующих индуктивности фильтра-прототипа вычисляются по формуле 2.8. Как показывают эксперименты, при такой аппроксимации краевую емкость разомкнутого конца полоскового волновода учитывать не следует. Поэтому длина волновода определяется по формуле 2.9. По данным расчета определяются конструктивные размеры элементов фильтра. Результаты расчета приведены в таблице 2.2. Таблица 2.2
Основная и дополнительная литератураОсновная: Микроэлектронные устройства СВЧ. Под ред. Г.И.Веселова – М.: Высшая школа, 1988 Конструкции СВЧ устройств и экранов. Под ред. А.Н.Чернушенко – М.: Радио и связь, 1983. Проектирование радиоприемных устройств/ Под ред. А.П.Сиверса – М.:Сов. Радио, 1976. Устройства управления амплитудой и фазой СВЧ сигналов: Учеб. пособие/ В.В.Фалин, Е.В.Федосеева, Е.И.Черныш; Под ред. В.В.Фалина: Муромский инст. Владим. гос. Ун-та. – Муром, 200. Полупроводниковые приборы. Сверхвысокочастотные диоды: Справочник/ Б.А.Наливайко. – Томск: МГП РАСКО, 1992. Полупроводниковые приборы. Транзисторы малой мощности: Справочник/ А.А.Зайцев, А.И.Миркин, В.В.Мокряков и др.; Под ред. А.В.Голомедова. – 2-е изд. – М.: Радио и связь, Кубк-а, 1995. Антенны и устройства СВЧ. Проектирование фазированных антенных решеток. Под ред. Д.И.Воскресенского. – М.: Радио и связь, 1994. Драбкин А.Л. и др. Антенно-фидерные устройства. – М.: Сов. радио,1974. Черныш Е.И. Зеркальные антенны: Учеб пособие – Муром: Муром. ин-т (фил.) Владим. гос.ун-та, 2001. Фельдштейн А.Л., Явич Л.Р., Смирнов В.П. Справочник по элементам волноводной техники. – М.:Сов. радио, 1967. Конструирование и расчеты полосковых устройств. Учебное пособие для вузов/Под ред. И.С.Ковалева. – М.: Сов. радио, 1974. Царапкин Д.П. Генераторы СВЧ на диодах Ганна. – М.:Радио и связь, 1982. Шварц Н.З. Линейные транзисторные усилители СВЧ.-М.: Сов. радио, 1980. Шварц Н.З.Усилители СВЧ на полевых транзисторах.- М.: Радио и связь, 1987. Бушминский И.П., Морозов Г.В. Технология гибридных интегральных схем СВЧ: Учеб. пособие. – М.: Высш. школа, 1980 Конструирование и технология микросхем. Курсовое проектирование: Учеб. пособие для вузов по спец. “Конструирование и производство радиоаппаратуры”/ Коледов Л.А., Волков В.А. и др.; Под ред. Л.А.Коледова. – М.: Высш. Школа, 1984. Воробьев Е.А. Расчет производственных допусков устройств СВЧ. – Л.: Судостроение, 1980. В.Д. Разевиг, Ю.В. Потапов, А.А. Курушин. Проектирование СВЧ устройств с помощью Microwave Office. Под ред. В.Д. Разевига. – М.: СОЛОН-Пресс, 2003. – 496 с.: ил. – (Серия «Системы проектирования»). Дополнительная: Филатов И.Н., Вакругов О.А., Панасенко П.В., Микроэлектронные СВЧ устройства. – М.: Высшая школа, 1978 (3 экз.) Справочник по расчету и конструированию СВЧ полосковых устройств. Под ред. В.И.Вольмана. – М.: Радио и связь, 1992.(2 экз.) Вайсблат А.В., Коммутационные устройства СВЧ на полупроводниковых диодах. – М.: Радио и связь, 1987 (5 экз.) Хижа Г.С., Вендикт И.В., Серебрякова Е.А. СВЧ фазовращатели и переключатели. – М.: Радио и связь, 1984. |
