Динамический режим средств измерения. Схема лабораторной установки
 Скачать 186.33 Kb.
|
|
Цель работы: изучение динамического режима средств измерений Схема лабораторной установки: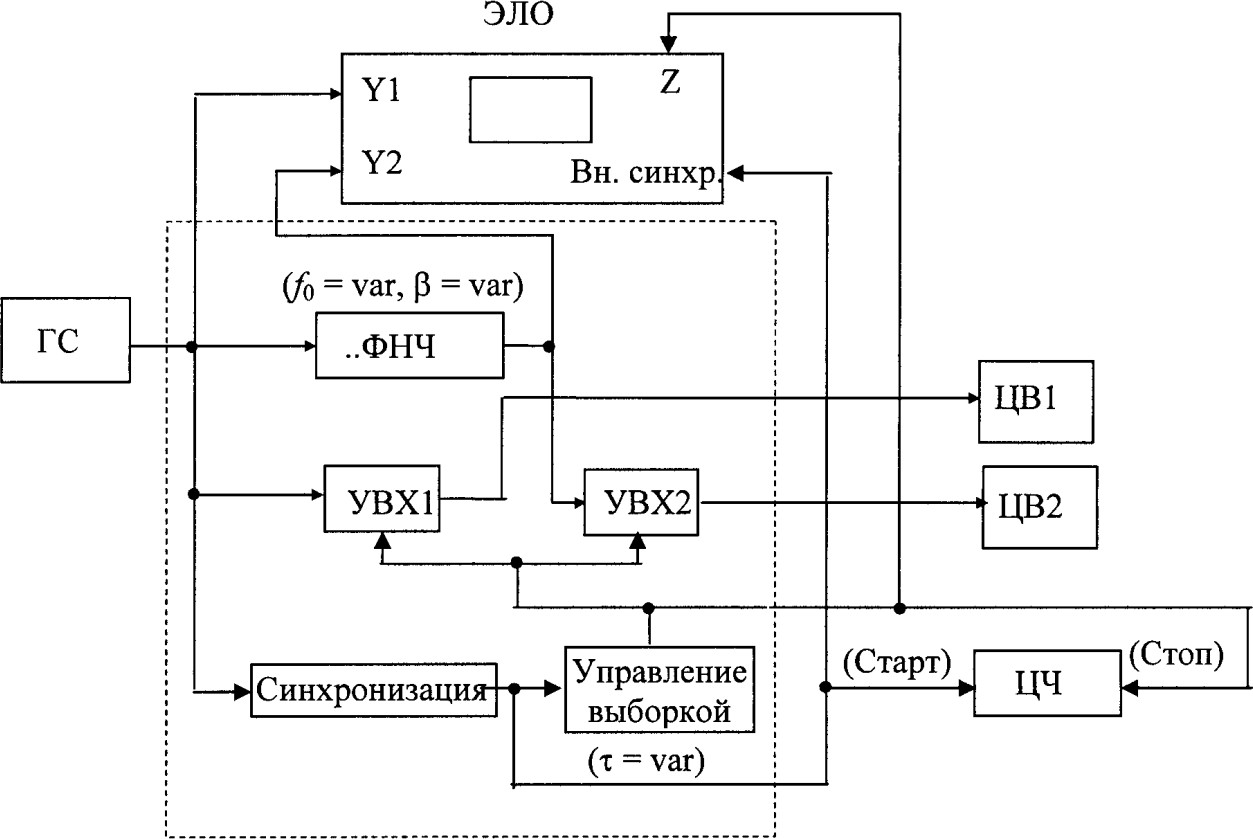 Рисунок 1. Схема лабораторной установки. ГС – генератор сигналов прямоугольной, синусоидальной и треугольной формы; ЦВ1 и ЦВ2 – цифровые вольтметры; ЦЧ – цифровой частотомер; ЭЛО – двухканальный электронно-лучевой осциллограф; устройства встроенные в горизонтальный пульт (в штриховой рамке): блок синхронизации; блок управления выборкой; УВХ1 и УВХ2 – устройства выборки и хранения мгновенных значений напряжений входного и выходного сигналов ФНЧ соответственно; ФНЧ – фильтр нижних частот; Теоретические положения:Изменение входного сигнала во времени влияет на результат измерений. Важным при этом являются характер изменение сигнала, т.е. его динамические свойства, и «скорость реакции» средства измерений на входное воздействие, определяемая динамическими характеристиками этого средства. В таких случаях говорят о динамическом режиме средств измерений. При анализе динамического режима средств измерения удобно рассматривать идеальные и реальные средства измерений, сопоставляя реакцию этих средств на одни и те же выходные воздействия. Идеальные в динамическом смысле средства измерения СИи, иначе безынерционные, имеют, как правило, линейную зависимость выходного сигнала yи(t)от входного x(t):yи(t)=kнx(t), где kн – номинальный коэффициент преобразования. Очевидно, что в таких средствах измерения выходной сигнал во времени полностью повторяет входной сигнал с точностью до множителя kн. В реальных средствах измерения СИр выходной сигнал y(t) в силу указанных причин будет иметь более сложную зависимость от входного сигнала, в частности, описываемую дифференциальными уравнениями соответствующего порядка. Разность между выходным сигналом y(t) реального средства измерений и выходным сигналом yи(t) (сигнал СИи) при одном и том же выходном сигнале x(t) определяет динамическую погрешность по выходу реального средства СИр измерений: ∆𝑦(𝑡) = 𝑦(𝑡) − 𝑦и(𝑡). (1) 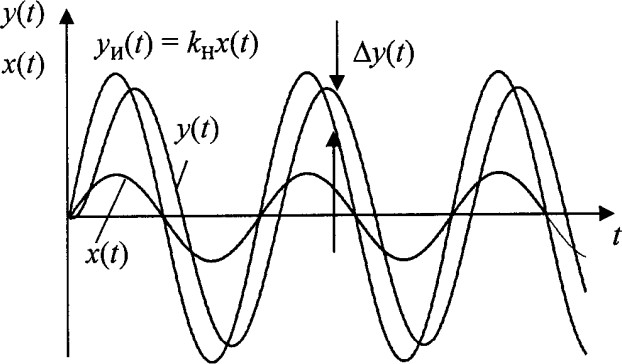 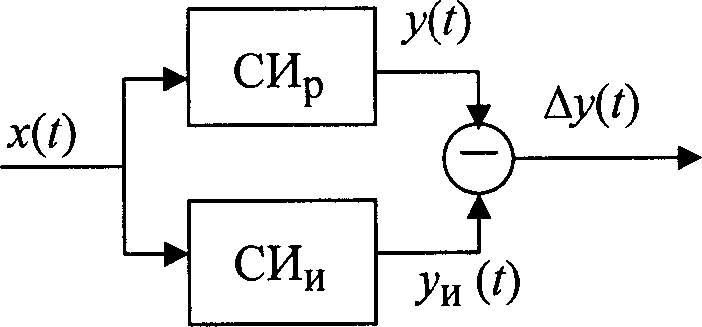 Замечание:в общем случае выражение (1) включает в себя и статистическую и динамическую погрешности средств измерений. Однако в данной работе будем считать, что статистическая погрешность пренебрежимо мала.Рисунок 2. Вариант сигналов измерений. Рисунок 3. Схема оценки динамической погрешности. Рисунок 2 иллюстрирует возможный вариант входного x(t) и выходных yи(t), y(t) сигналов идеального и реального средств измерений и возникающую при этом динамическую погрешность ∆y(t). На рис. 3 показана структурная схема, удобная для интерпретации и оценки возникающей динамической погрешности. Спецификация применяемых средств измерений:
Протокол наблюдений к лабораторной работе №6«Динамический режим средств измерения» Затухающий сигнал: Kp=1 мс/дел; k0=2 В/дел; f0=0,4 кГц; ß=0,3
 Время установления:
Два синусоидальных сигнала: f0=0,4 кГц; ß=2
Обработка результатов:1. Определим динамическую погрешность при ступенчатом входном воздействии, ∆𝑈(𝑡) = 𝑈вых(𝑡) − 𝑈вх(𝑡) t’=Kpt Таблица 1. Динамический режим измерений при прямоугольном воздействии.
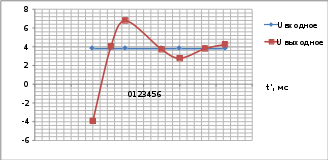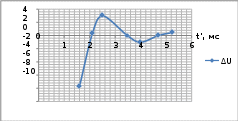Пример расчёта: ∆𝑈(1,6) = 𝑈вых(1,6) − 𝑈вх(1,6) = −3,93 − 3,79 = −7,72; U, B  ∆𝑈(2,1) = 𝑈вых(2,1) − 𝑈вх(2,1) = 4,03 − 3,79 = 0,24. ∆U, B  Рисунок 4. Графики входного и выходного сигналов при ступенчатом воздействии. Рисунок 5. График динамической погрешности при ступенчатом воздействии. Построение графика зависимости времени установления для различных частот при заданном коэффициенте демпфирования: ty , мс 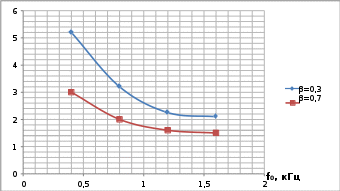 Таблица 2. Зависимость времени установления от частоты.
Рисунок 6. График зависимости времени установления от частоты. Построение графика зависимости времени установления для различных коэффициентов демпфирования при заданной частоте: Таблица 3. Изменение времени установления от коэффициента демпфирования.
ty , мс 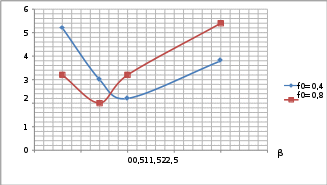 Рисунок 7. График зависимости времени установления от коэффициента демпфирования.3. Определим динамическую погрешность при входном синусоидальном воздействии, ∆𝑈(𝑡) = 𝑈вых(𝑡) − 𝑈вх(𝑡) t’=Kpt Таблица 4. Динамический режим при синусоидальном воздействии
Пример расчёта: ∆𝑈(0) = 𝑈вых(0) − 𝑈вх(0) = 1.68 − 2.89 = −1.21; ∆𝑈(1) = 𝑈вых(1) − 𝑈вх(1) = 3.06 − 3,90 = −0,84. U, B ∆U, B 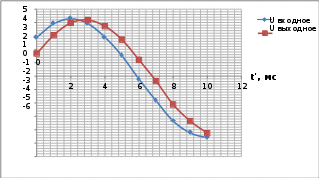 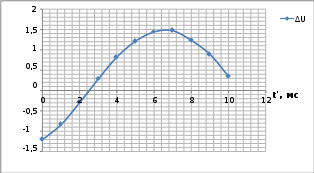 Рисунок 8. Графики входного и выходного сигналов при синусоидальном воздействии. Рисунок 9. График динамической погрешности при синусоидальном воздействии. Вывод: в ходе лабораторной работы был изучено понятие динамического режима измерений и динамической погрешности. При анализе данных было выявлено, что при увеличении частоты колебаний время установления уменьшается, а при увеличении коэффициента демпфирования время сначала уменьшается, пока не дойдёт до своего минимального значения, а потом растёт вместе с коэффициентом демпфирования. При синусоидальном режиме динамическая погрешность меняется по закону, похожему на синусоидальный. При ступенчатом воздействии динамическая погрешность стремиться к нулю по мере продолжительности сигнала. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||