задачи. Задача 1 и 2. Наименование предприятия Дивидендная доходность,%

• Название: Наименование предприятия Дивидендная доходность,%
• Анкор: задачи
• Дата: 23.02.2023
• Размер: 28.1 Kb.
• Имя файла: Задача 1 и 2.docx
• Тип: Задача; #952093

Задача 1

№п/п	Наименование предприятия	Дивидендная доходность,%	Доля в портфеле
1	ОАО Газпром	5,5	0,05
2	ОАО Лукойл	6	0,2
3	ОАО Сбербанк	4	0,25
4	ОАО Роснефть	4,5	0,2
5	ОАО Аэрофлот	4,45	0,15
6	ОАО Ростелеком	3,6	0,1
7	ОАО Банк ВТБ	3,2	0,05

Решение

Суть расчета коэффициента вариации состоит в том, что по множеству значений рассчитывается сначала среднее квадратичное отклонение, а затем – среднее арифметическое, а после – найти их соотношение.

В общем виде формула расчета коэффициента вариации выглядит следующим образом:

CV = σ / t ср

CV – коэффициент вариации;

σ – среднее квадратическое отклонение;

t – среднее арифметическое значение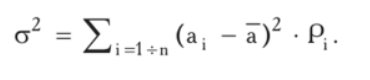



Средняя=(5,5+6+4+4,5+4,45+3,6+3,2)/7=4,46

σ²=(5,5-4,46)2*0,05+(6-4,46)2*0,2+(4-4,46)2*0,25+(4,5-4,46)2*0,2+(4,45-4,46)2*0,15+(3,6-4,46)2*0,1+(3,2-4,46)2*0,05=17,88

σ=4,23

t=(5,5*0,05+6*0,2+4*0,25+4,5*0,2+4,45*0,15+3,6*0,1+3,2*0,05)/7=0,65

CV = 4,23/0,65=6,49

Задача 2

Состояние экономики	Вероятность	Доходность инвестиций, % годовых
		проект 1	проект II
Глубокий спад	0,05	-3,0	-2,0
Спад	0,20	6,0	9,0
Стагнация	0,50	11,0	12,0
Подъем	0,20	14,0	15,0
Сильный подъем	0,05	19,0	26,0

Решение

Дисперсия дискретного распределения (а²):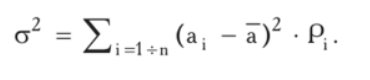



Дисперсия — это сумма квадратов отклонений от ожидаемого значения, взвешенная на вероятность каждого отклонения.

Средняя1=-3+6+11+14+19/5=9,4

Средняя 2=-2+9+12+15+26/5=12

σ1²=(-3-9,4)2*0,05+(6-9,4)2*0,2+(11-9,4)2*0,5+(14-9,4)2*0,2+(19-9,4)2*0,5=19,31

σ2²=(-2-12)2*0,05+(9-12)2*0,2+(12-12)2*0,5+(15-12)2*0,2+(26-12)2*0,5=23,2

Другим измерителем разброса индивидуальных значений вокруг среднего является среднее квадратическое, или стандартное, отклонение, представляющее собой квадратный корень из дисперсии: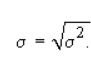



Среднее квадратическое отклонение доходности первого проекта составит: 

σ1=4,39%

второго:

σ2=4,82%

Коэффициент вариации — йота-коэффициент как измеритель риска.

Этот коэффициент, который часто называют йота-коэффициентом, представляет собой отношение среднего квадратического отклонения к ожидаемому значению доходности: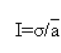



где I — коэффициента вариации — йота-коэффициент;

а — среднее квадратическое отклонение доходности.

I1=4,39/9,4=0,46

I2=4.82/12=0.4

Полученные результаты позволяют сделать важный вывод: второй из двух альтернативных проектов обеспечивает не только большую доходность, но и более низкий относительный риск, поэтому он является предпочтительным.