индивидуальный проект. Инд проект Данил. Графы и их применение
 Скачать 1.11 Mb.
|
|
Министерство образования и молодёжной политики Чувашской Республики Государственное автономное профессиональное образовательное учреждение Чувашской Республики «Батыревский агропромышленный техникум» Индивидуальный проект по математике на тему : «Графы и их применение» студентов 1 курса обучающегося по специальности, профессии 26.01.21 Мастер общестроительных работ Шакеева Сергея, Чернова Андрея Оценка работы:________________________ Преподаватель: Кучерова Татьяна Германовна Подпись:______________________________ Дата:_________________________________ Батырево,2021г. Содержание: I. Введение…………………………………………………………………..…2 II. Основная часть. 1.История возникновения теории графов…………………………………….4 2.Основные понятия теории графов…………………………………………..5 3.Некоторые задачи теории графов…………………………………………...6 3.1 Задачи о вычерчивании фигур одним росчерком………………………..8 3.2 Задачи с лабиринтами……………………………………………………..10 3.3 Логические задачи…………………………………………………………12 4.Применение теории графов в различных сферах деятельности…………..15 4.1.Графы и история……………………………………………………………17 4.2.Графы и химия……………………………………………………………...18 4.3. Графы и физика…………………………………………………………….19 III. Заключение…………………………………………………………………..20 IV. Список литературы………………………………………………………..…21 Введение Всем известна занимательная задачка про открытый конверт: «Начертите фигуру, не отрывая карандаша от бумаги и не проводя никакую линию дважды».  В этом году я был участником дистанционной олимпиады по математике. В ней была предложена такая задача: «Почтальон Печкин разнёс почту во все дома деревни, после чего зашёл к дяде Фёдору выпить молока. На рисунке показаны все тропинки, которые проходил Печкин, причём как оказалось, ни одной из них он не проходил дважды. Каким маршрутом шёл почтальон Печкин? В каком доме живёт дядя Фёдор?»                     Разбирая решение этой задачи, я задался вопросом: «Можно ли решить эти задачи не перебором, а другим, более быстрым, способом?» После этого я обратился к своему учителю, и мне объяснили, что решить эту задачу я могу, изучив теорию графов. Но прежде, чем найти ответ на свой вопрос, я увидел, что теория графов помогает упростить решение многих задач. Графы заинтересовали меня своей возможностью помогать в решении различных головоломок, математических и логических задач. Цель: показать применение теории графов для решения различных видов задач Задачи: Изучить элементы теории графов. Разобрать решение различных видов задач. Узнать о применении графов в науке и в различных сферах деятельности. Методы исследования: Поиск и анализ информации в литературе. Поиск и изучение информации в интернет – ресурсах. Моделирование. II Основная часть 1. История возникновения теории графов. Датой рождения теории графов принято считать 1736 год, когда Леонард Эйлер решил задачу о кенигсбергских мостах (Приложение 1.). Ру 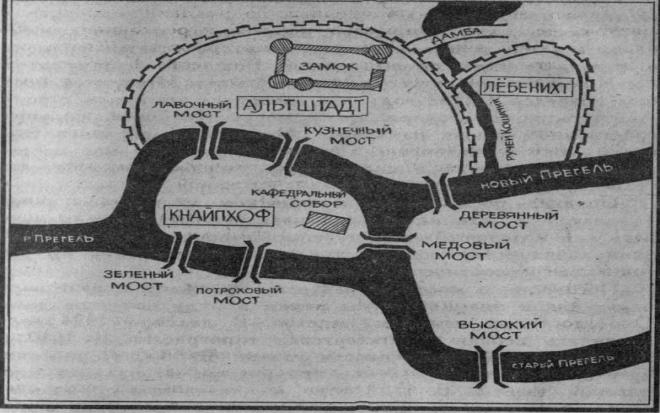 кава реки Прегель, на берегу которой расположен город Кенигсберг, образовывали два острова. В эту эпоху четыре образовавшихся участка суши (правый и левый берег и два острова) соединяло семь мостов так, как это показано на рисунке. Горожане, гуляя по городу, пытались составить маршрут, чтобы он проходил по каждому мосту ровно один раз. Это им не удавалось, а Эйлер доказал, что это принципиально невозможно.Термин «граф» впервые ввел в 1936 году венгерский математик Денеш Кениг. Широкое развитие теория графов получила в 50-х годах 20 века в связи со становлением кибернетики и развитием вычислительной техники. Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. С дворянским титулом «граф» их связывает общее происхождение от латинского слова «графио» - пишу. 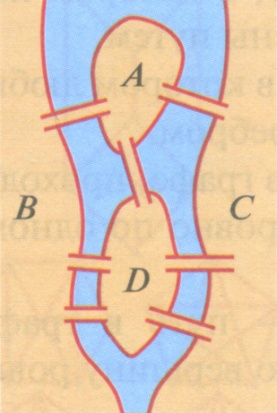 2. Основные понятия теории графов. В математике определение графа дается так: «графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами».  Схема графа, состоящая из «изолированных» вершин, называется нулевым графом. (рис.2) Графы, в которых не построены все возможные ребра, называются неполными графами. (рис.3) Графы, в которых построены все возможные ребра, называются полными графами. (рис.4)    Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной. Если степени всех вершин графа равны, то граф называется однородным. Таким образом, любой полный граф — однородный. На рисунке 5 изображен граф с пятью вершинами. Степень вершины А обозначим Ст.А. На рисунке 5 : Ст.А = 1, Ст.Б = 2, Ст.В = 3, Ст.Г= 2, Ст.Д= 0. 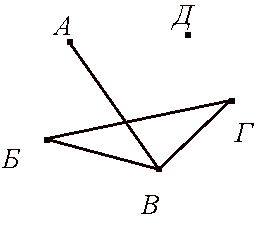 рис.5 3. Некоторые задачи теории графов. Эйлеров путь - путь в графе, проходящий через каждое ребро ровно один раз. Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. (рис.6) Такими графы названы в честь учёного Леонарда Эйлера. 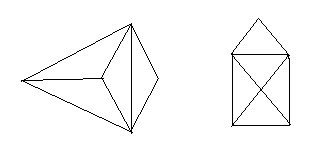 рис.6 (эйлеровы графы)Закономерность 1. Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине. Закономерность 2. Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них. Закономерность 3. Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком». Фигура (граф), которую можно начертить, не отрывая карандаш от бумаги, называется уникурсальной. Алгоритм решения Из предыдущих рассуждений мы получаем общий прием решения каждой подобной задачи о мостах: преобразовать рисунок в граф (определить его вершины и рёбра); определить степень каждой вершины; посчитать количество нечётных вершин; сделать выводы: а) заданный обход возможен, если - все вершины чётные (его можно начать с любой вершины); - две вершины нечётные (его нужно начать с одной из нечётных вершин); б) заданный обход невозможен, если нечётных вершин больше двух; указать начало и конец пути. Я, изучив эти выводы, решил проверить их на примерах задач из раздела теории графов. 3.1. Решение задач о вычерчивании фигур одним росчерком Задача №1 (О кенигсбергских мостах). Че  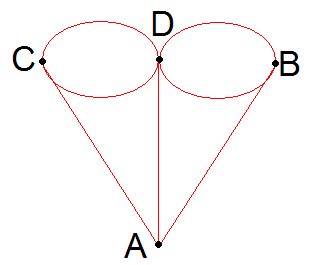тыре образовавшихся участка суши (правый и левый берег и два острова) соединяло семь мостов так, как это показано на рисунке. Горожане пытались составить маршрут, чтобы он проходил по каждому мосту ровно один раз.Решение. Эту задачу решил Леонард Эйлер. Он построил следующий граф и получил, что все четыре вершины нечетные, то есть нельзя пройти по всем мостам один раз и закончить путь там, где он был начат. Задача №2. Можно ли нарисовать графы, изображенные на рисунках, не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз? Р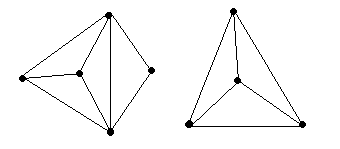е  шение:Можно, т. к. только 2 нечетные вершины. Нельзя, т. к. 4 нечетные вершины. За 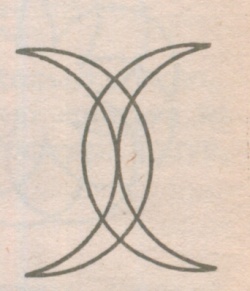 дача №3.Говорят, что Магомет вместо подписи (он был неграмотен) описывал одним росчерком состоящий из двух рогов луны знак, представленный на рисунке. Возможно ли это? Решение. Да, потому что в данном случае мы имеем дело с вершинами четного порядка. 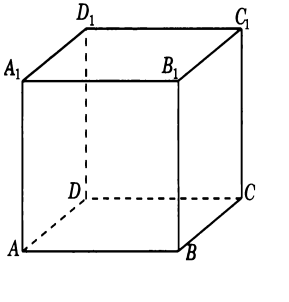 Задача №4. (Муха в банке). Муха забралась в банку из-под сахара. Банка имеет форму куба. Сможет ли муха последовательно обойти все 12 ребер куба, не проходя дважды по одному ребру? Подпрыгивать и перелетать с места на место не разрешается. Решение. Ребра и вершины образуют граф, все 8 вершин которого имеют 3 степень, и, следовательно, требуемый обход невозможен. Задача №5. (Путь Печкина) 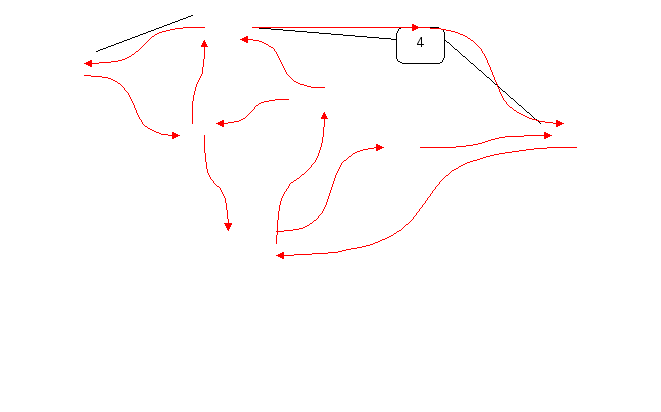 Решение. Нечётных вершин в условии задачи две – почта и дом, поэтому начинаться и заканчиваться маршрут может только в этих узлах. Почтальон Печкин начинает разнос писем с почты, поэтому его маршрут может заканчиваться в доме 5, там и живёт дядя Фёдор. Например, маршрут может быть таким: почта-1-3-2-1-7-почта-3-4-5-7-6-5. Задачи с лабиринтами Кроме задач вида «одним росчерком» полученным способом можно решать задачи с лабиринтом. Происхождение задач о лабиринтах относится к глубокой древности и теряется во мраке времен. Слово «лабиринт» (греческое) означает «ходы в подземельях». Решению задачи о лабиринтах предпосылаются исторические справки – чтобы показать интерес к этой задаче и дать наглядное представление о существовавших и существующих лабиринтах. Задача о прохождении лабиринта приобретает практический интерес, поскольку устройство линий электропередач, канализации, сетей дорог, каналов и т.д. – все это более или менее сложные лабиринты. Начало решению вопроса о существовании безвыходных лабиринтов положено Эйлером. Нарисовав соответствующий лабиринту граф, используют способ обхода всех ребер для нахождения выхода. Решение (т.е. маршрут, ведущий к цели) каждого лабиринта может быть найдено одним их трех сравнительно простых методов. Первый метод – МЕТОД ПРОБ И ОШИБОК. Выбирайте любой путь, а если он заведет вас в тупик, то возвращайтесь назад и начинайте все сначала. Второй метод – МЕТОД ЗАЧЕРКИВАНИЯ ТУПИКОВ. Начнем последовательно зачеркивать тупики, т.е. маршруты, не имеющие ответвлений и заканчивающиеся перегородкой. Незачеркнутая часть коридоров будет выходом или маршрутом от входа к выходу или к центру. Третий метод – ПРАВИЛО ОДНОЙ РУКИ. Оно состоит в том, что по лабиринту надо двигаться, не отрывая одной руки (правой или левой) от стены. Рассмотрим задачу общего вида: Мо  жно ли обойти все данные комнаты, пройдя через каждую дверь ровно один раз и выйти на улицу через комнату 1 или 10? С какой комнаты надо начинать?Решение: Пу  сть комнаты – вершины графа, а двери – ребра. Проверим степени вершин:Только две вершины имеют нечетную степень. Начать движение можно из комнаты 10, а закончить в комнате 8, либо наоборот. Но, чтобы выйти на улицу (из комнаты 10), надо начинать из комнаты 8. В этом случае пройдём все двери один раз и попадём в комнату 10, но окажемся внутри комнаты, а не снаружи:  Аналогично рассуждая, можно решать любые задачи с лабиринтами, входами и выходами, подземельями и т.п. 3.3 Логические задачи Задача №1. Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано? Решение: Пу  сть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена.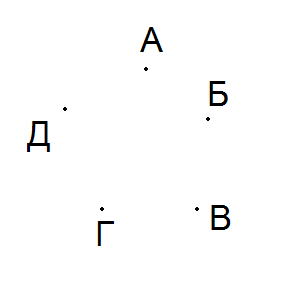 Если подсчитать число ребер графа, изображенного на рисунке справа, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10. Задача №2. В 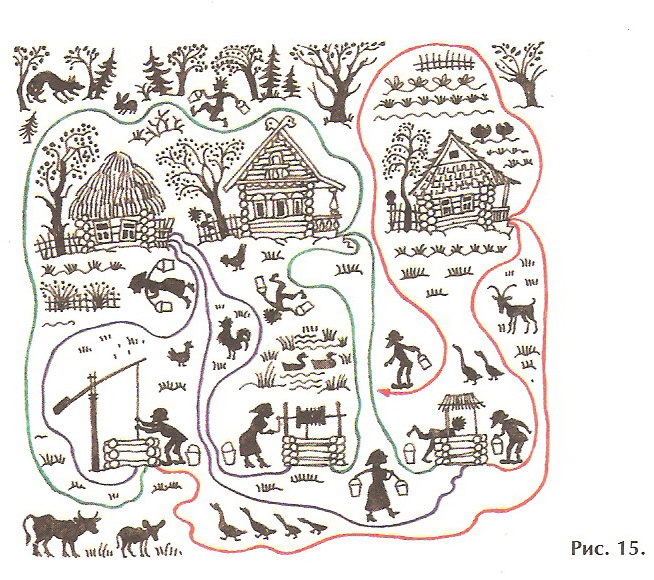 деревне 10 домов, и из каждого выходит по 7 тропинок, идущих к другим домам. Сколько всего тропинок приходит между домами?Решение. Пусть дома- вершины графа, тропинки- рёбра. По условию из каждого дома (вершины) выходит 7 тропинок (рёбер), тогда степень каждой вершины 7, сумма степеней вершин 7×10=70, а число рёбер 70 : 2= 35. Таким образом, между домами проходит 35 тропинок. Ответ. 35 тропинок Задача №3. В одном дворе живут четыре друга. Вадим и шофер старше Сергея, Николай и слесарь занимаются боксом, электрик-младший из друзей. По вечерам Андрей и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей. Решение. Составим граф из 4 друзей и 4 профессий. Пунктирными линиями отметим невозможные связи, а сплошной - соответствие имени и профессии. Если от каждой вершины выходить 3 пунктирных линии, то четвертая линия должна быть сплошной.   В С Н А               Ш С Т Э Задача №4. В небольшом городке живут пять друзей: Иванов, Петренко, Сидорчук, Гришин и Капустин. Профессии у них разные: один из них маляр, другой- мельник, третий- плотник, четвертый-почтальон, а пятый- парикмахер. Петренко и Гришин никогда не держали в руках малярной кисти. Иванов и Гришин собираются посетить мельницу, на которой работает их товарищ. Петренко и Капустин живут в одном доме с почтальоном. Сидорчук был недавно в ЗАГСе одним из свидетелей, когда Петренко и дочь парикмахера сочетались законным браком. Иванов и Петренко каждое воскресенье играют в городки с плотником и маляром. Гришин и Капустин по субботам обязательно встречаются в парикмахерской, где работает их друг. Почтальон предпочитает бриться сам. Кто есть кто? Генеалогическое дерево А.С. Пушкина. 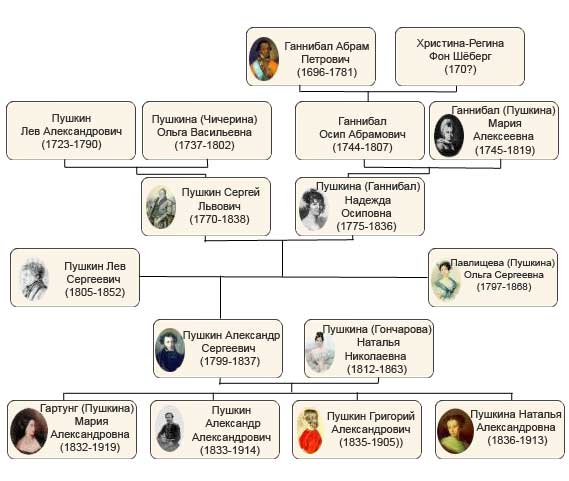 Моё генеалогическое дерево  4.1.Графы и химия. Теория графов в химии применяется для решения различных теоретических и прикладных задач. Применение графов теории базируется на построении и анализе различных классов химических и химико-технологических графов, которые называются также топология, т.е. модели, учитывающие только характер связи вершин. Ребра и вершины этих графов отображают химические и химико-технологические понятия, явления, процессы или объекты и соответственно качественные и количественные взаимосвязи либо определенные отношения между ними. Пр 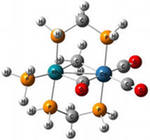 и графическом изображении формул веществ указывается последовательность расположения атомов в молекуле с помощью, так называемых валентных штрихов (термин «валентный штрих» предложил в 1858 г. А. Купер для обозначения химических сил сцепления атомов), иначе называемых валентной чертой (каждая валентная черта, или валентный штрих, эквивалентны одной паре электронов в ковалентных соединениях или одному электрону, участвующему в образовании ионной связи).Химические графы дают возможность прогнозировать химические превращения, пояснять сущность и систематизировать некоторые основные понятия химии. Молекулярные графы, применяемые в стереохимии и структурной топологии, химии кластеров, полимеров и др., представляют собой неориентированные графы, отображающие строение молекул. Вершины и ребра этих графов отвечают соответственно атомам и химическим связям между ними. Мо 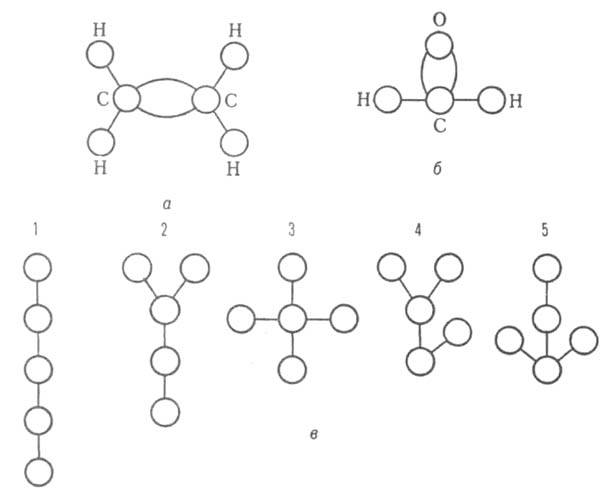 лекулярные графы и деревья: а, б - мультиграфы этилена и формальдегида; в-молекулы изомеров пентана.4.3.Графы и физика Ещ 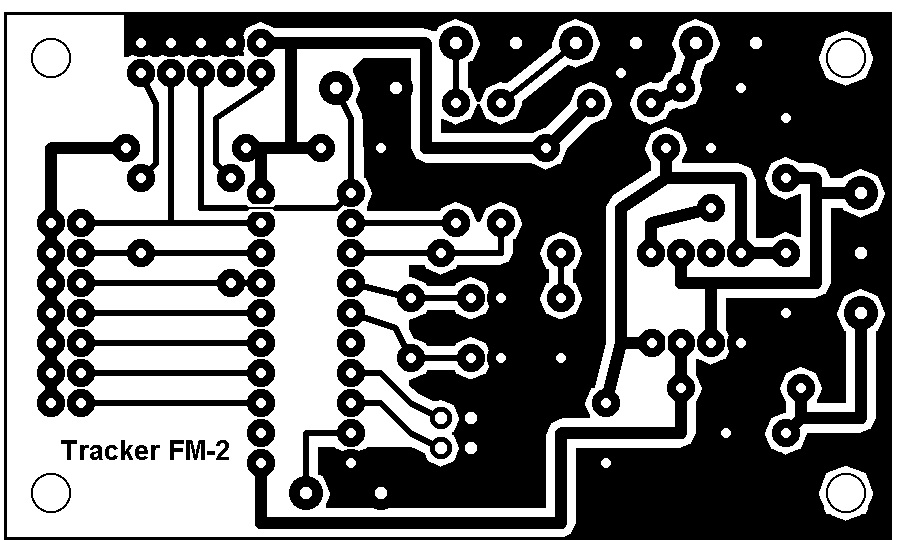  е недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем.Печатной схемой называют пластинку из какого-либо диэлектрика (изолирующего материала), на которой в виде металлических полосок. вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы, их пересечение в других местах вызовет замыкание электрической цепи. В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках. Изучая этот материал, я узнала области применения теории графов и сделала вывод, что этот раздел математики является одним из важнейших, который используется в нашей повседневной жизни часто незаметно для нас. III Заключение. Чтобы найти ответ на интересующую меня задачу, мне пришлось познакомиться с новым разделом математики «Теорией графов», который не изучается в школьном курсе, но облегчает решение многих задач, я узнал много нового, понял, что математика интересна, но и трудна. Изучая этот материал, я узнал области применения теории графов и сделал вывод, что этот раздел математики является одним из важнейших, который используется в нашей повседневной жизни часто незаметно для нас. Графы – это замечательные математические объекты, с помощью, которых можно решать математические, логические и экономические задачи. Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту. Многие математические доказательства также упрощаются, приобретают убедительность, если пользоваться графами. Также можно решать различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Графы используются при составлении карт и генеалогических древ. IV. Литература. 1. Альхова З.Н., Макеева А.В. Внеклассная работа по математике. – Саратов: «Лицей», 2002 г. 2. Перельман Я.И. Одним росчерком. – Ленинград, 1940 3. Башмаков М. И. Математика в кармане «Кенгуру». - М.: Дрофа, 2010г. 4. Игнатьев Е. И. Математическая смекалка. - М.: «Омега», 1994г. 5. Подготовка школьников к олимпиадам по математике. 5-6 классы./сост. Григорьева Г.И. – М. : «Глобус», 2009 г. |