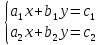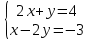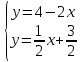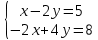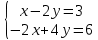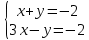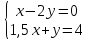Главная страница
Навигация по странице:

  • Перед уроком распечатать алгоритм и рабочие листы (с. 3-6 технологички) по числу учащихся на уроке

  • Проверить дом. задание в тетрадях

  • Решим систему уравнений

  • Рабочие листы подписать!

  • Алгоритм графического решения системы двух линейных уравнений с двумя переменными

    		•

    Урок 7 кл алгебра графический способ решения СЛУ. Графический способ решения системы линейных уравнений


    Скачать 1.35 Mb.
    НазваниеГрафический способ решения системы линейных уравнений
    Дата26.12.2022
    Размер1.35 Mb.
    Формат файлаdocx
    Имя файлаУрок 7 кл алгебра графический способ решения СЛУ.docx
    ТипУрок
    #864774

    Урок


    1. Тема: Графический способ решения системы линейных уравнений

    2. Цель: Изучить графическое представление системы линейных уравнений и ее решения

    3. Задачи: Иметь представление о взаимном расположении графиков линейных уравнений с двумя неизвестными

    4. Тип урока: ОНЗ

    Перед уроком распечатать алгоритм и рабочие листы (с. 3-6 технологички) по числу учащихся на уроке

    Этап
    Время, мин.
    Деятельность учителя
    Деятельность учеников

    1. Организационный момент
    1
    Приветствовать учащихся
    Успокоиться, приветствовать учителя, занять свои места, настроиться на работу на уроке.

    2. Проверка домашнего задания
    7
    Проверить дом. задание в тетрадях

    Ответить на вопросы:

    1) Что называется решением системы уравнений с двумя переменными?

    2) Что значить решить систему уравнений?

    3) Сколько решений может иметь система линейных уравнений с двум переменными?

    4) Написать на доске общий вид системы линейных уравнений с двумя переменными.
    Вспомним, как строить график линейной функции по-американски (серьезно)

    1. Отметить на OY точку с координатой равной свободному члену b;

    2. Откладывать от этой точки:

    - 1 клетку вправо и k клеток вверх, если k - целое положительное:

    - 1 клетку влево и k клеток вверх, если k - целое отрицательное

    - столько клеток вправо, сколько стоит в знаменателе и столько клеток вверх, сколько стоит в числителе, если k - обыкновенная дробь больше нуля

    - столько клеток влево, сколько стоит в знаменателе и столько клеток вверх, сколько стоит в числителе, если k - обыкновенная дробь меньше нуля (видео приложу, дети его видели, но не помнят...)
    1) Решением системы уравнений с двумя переменными называется такая пара чисел, которые, при подстановке в оба уравнения системы, превращают их в верные числовые равенства

    2) Решить систему уравнений - значит, найти все ее решения или доказать, что решений нет.

    3) Система линейных уравнений может иметь единственное решение, не иметь решения (быть несовместной) или иметь бесконечное множество решений (быть неопределенной)

    4)

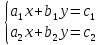
    3. Подготовка к основному этапу урока
    10
    Решим систему уравнений

    (учитель строит на доске, учащиеся в тетради)



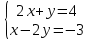
    Приводим оба уравнения к виду y=kx+b



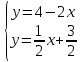
    Построим в одной системе координат графики обоих уравнений.

    Так как k1 ≠ k2, то прямые пересекаются (не параллельны и не совпадают).

    На графике отметим точку пересечения прямых, найдем ее координаты (А (1; 2))

    Напомним, координаты точки на плоскости сначала указывают по OX, а затем по OY.
    Записывают алгоритм графического решения системы линейных уравнений с двумя неизвестными (см. Алгоритм), на доске под руководством учителя решают 2 системы:

    1)

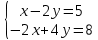
    Делают вывод о том, что прямые параллельны, и система несовместна, т.к. общих точек у прямых нет.
    2)

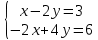
    Делают вывод о том, что прямые совпадают, и система неопределена, т.к. все множество точек прямой является решением.

    4. Основной этап работы
    12
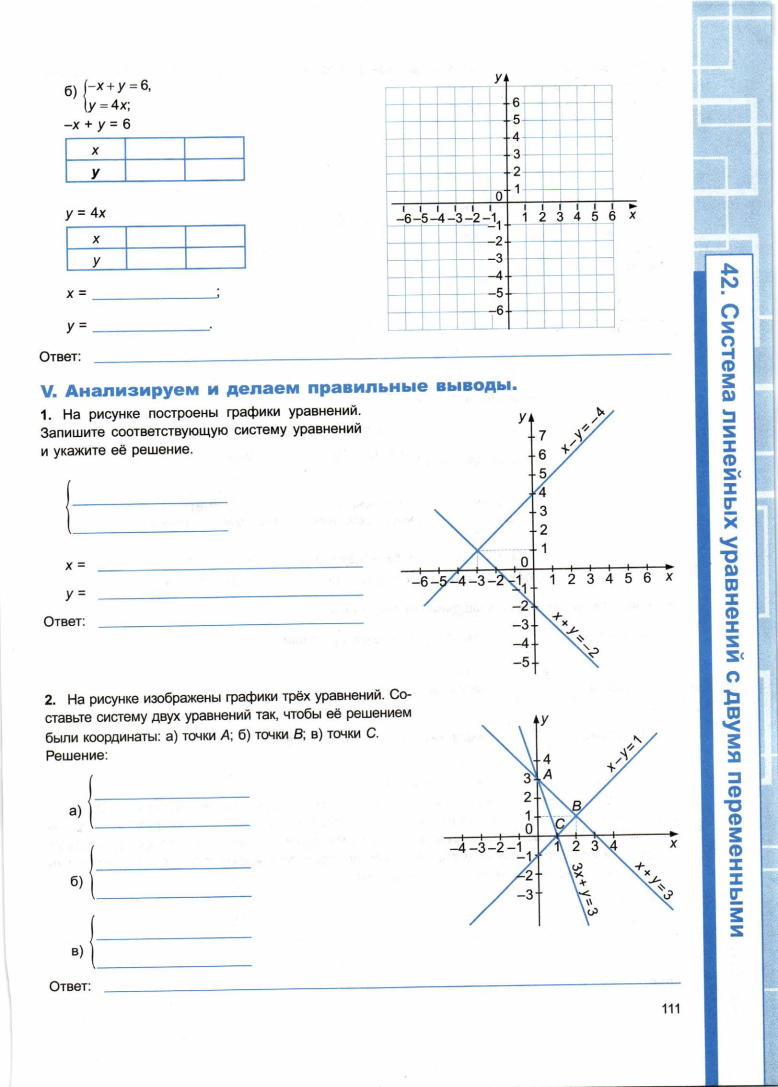
    Решить задания 2 и 3 на рабочих листах.

    Рабочие листы подписать!
    Решают задания 2 и 3 на рабочих листах;

    Раздел V, задания 1 и 2 - для Павла и Дениса.

    5. Закрепление полученных знаний
    5
    Решить графическим способом систему линейных уравнений:
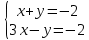
    Один учащийся решает на доске, остальные в тетради по алгоритму

    6. Обобщение и систематизация
    5
    Решить самостоятельно графически систему линейных уравнений:
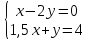
    Решают самостоятельно систему в тетрадях по алгоритму

    7. Контроль и самопроверка знаний
    3



    Показать решенную в тетради систему уравнений

    8. Подведение итогов урока
    2
    выполнить задания 3 и 4 на рабочем листе.
    Подать дневники под оценки; записать домашнее задание.

    Алгоритм графического решения системы двух линейных уравнений с двумя переменными

    1. Привести оба уравнения к стандартному виду:



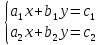
    2. Привести оба уравнения к виду формулы линейной функции:



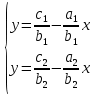
    3. Построить графики обеих функций в одной системе координат:

    а) заполнить таблицу с координатами 2 точек для первой функции:

    x






    y






    Нанести точки на координатную плоскость, провести через них прямую

    б) заполнить таблицу с координатами 2 точек для второй функции:

    x






    y






    Нанести точки на координатную плоскость, провести через них прямую

    4. Найти точку пересечения прямых, обозначить ее координаты

    Выписать ответ в виде пары чисел в скобках (xA; yA),

    где xA- координата по оси OX, yA - координата по оси OY

    ИЛИ

    - записать "Система несовместна", если прямые параллельны;

    - Записать "Система неопределена", если прямые совпадают.

    написать администратору сайта