Путин гравиразведка. Гравитационное поле земли
 Скачать 1.58 Mb. Скачать 1.58 Mb.
|
|
ГРАВИТАЦИОННОЕ ПОЛЕ ЗЕМЛИ Сила, потенциал и градиенты поля силы тяжести Земли. 1.1 Сила тяготения и ее потенциал. Основные виды и свойства потенциала силы тяготения Все мы хорошо знаем, что Вселенная является чрезвычайно сложным организмом, населенным множеством различных тел, планет, частиц, взаимодействующих друг с другом. Взаимодействие обитателей Вселенной происходит, в основном, через физические поля: электромагнитные, силовые, ядерные, температурные, плотностные и т.д., каждое из которых решает определенную роль в общем функционировании организма Вселенной. Так как гравиметрия изучает поле силы тяжести, то сделаем акцент на силовые поля. Каждое силовое поле характеризуется силой и потенциалом силы. При этом под потенциалом силы понимают некоторую вспомогательную функцию, частные производные которой по осям координат равны проекциям силы на эти оси. Обозначив потенциал через R, а силу через G, запишем математическое выражение для потенциала согласно его определению:  Понятие потенциала силы введено для удобства решения практических задач гравиметрии, в чем мы убедимся в дальнейшем. Графически каждое силовое поле представляется в виде силовых линий и уровенных поверхностей (рис. 2). Силовые линии - это линии, в каждой точке которых касательная совпадает с направлением вектора силы. Поверхности, всюду перпендикулярные силовым линиям, называются уровенными или изопотенциальны- ми поверхностями.  Так как геодезия неразрывно связана с гравитационным полем Земли, которое характеризуется силой тяжести, слагаемой из силы тяготения (притяжения) и центробежной силы, и ее потенциалом, то приступим к рассмотрению всех этих сил. Сила тяготения. Понятие силы тяготения хорошо известно из школьного учебника физики. Вспомним закон всемирного тяготения Исаака Ньютона (1643 - 1727 гг.), согласно которому все тела притягиваются друг к другу с силой, пропорциональной произведению масс взаимодействующих тел и обратно пропорциональной квадрату расстояния между ними, то есть согласно рис. 3 можно записать:  В (2.2) F - сила тяготения; т| - притягивающая масса; т2 - притягиваемая масса; г - расстояние между взаимодействующими массами; f - гравитационная постоянная. Выражение (2.2) записано в скалярном виде, знак «минус» означает, что сила направлена от притягивающей массы к притягиваемой. В векторном виде закон всемирного тяготения представлен выражением  Гравитационная постоянная f определяется с помощью крутильного маятника. Ее численное значение равно, соответственно, в системах CGS и СИ:  Гравитационная постоянная не зависит от физических и химических свойств взаимодействующих масс, расстояния между ними, направления и скорости их движения (при условии, что эти скорости не приближаются к скорости света), а также свойств среды, расположенной между массами. Потенциал силы тяготения. Его основные виды Потенциал силы тяготения F есть некоторая вспомогательная функция V, частные производные которой по осям координат равны проекциям силы тяготения на эти оси. Математическое выражение для потенциала силы тяготения имеет вид:  Наиболее употребляемые на практике простейшие виды потенциала силы тяготения, к которым при математических выкладках сводится большинство случаев, являются: потенциал тяготения точечной массы; потенциал тяготения объемных масс; потенциал тяготения простого слоя. Потенциал тяготения точечной массы т. Для уяснения этого понятия приведем чертеж (рис. 4). Пусть в точке М с координатами (<д Ь, с) расположена точечная масса т, а в точке Р с координатами (х, у, z) расположена единичная масса тщ = 1. Потенциал тяготения точечной массы в этом случае будет равен Докажем формулу (2.5). Доказательство будем вести, исходя из определения потенциала силы тяготения, согласно которому для выражения (2.5) должны быть справедливыми равенства (2.4). С этой целью запишем закон всемирного тяготения для случая, представленного на рис. 4, в виде выра- dV dV dV жения (2.6) и возьмем частные производные —; —; —. дх ду dz    Следовательно, выражение (2.5) действительно есть выражение для потенциала силы тяготения точечной массы. Потенциал тяготения объемных масс или тела. Для вывода формулы для потенциала тела поступим следующим образом. Разобьем притягивающую массу М на бесконечно большое число элементарных масс dm, которые будем рассматривать как точечные массы (рис. 5). 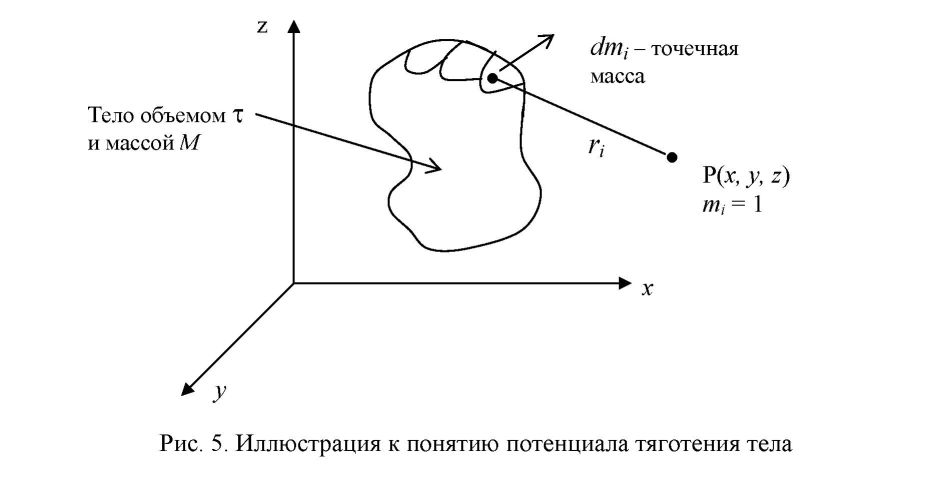 Потенциал тяготения элементарной массы, находящейся в текущей точке, для точки Р будет равен  Из (2.15) следует, что для определения потенциала тяготения тела необходимо знать форму поверхности, ограничивающей данное тело, и плотность в каждой точке как внутри тела, так и на его поверхности. Потенциал тяготения простого слоя. Вначале уясним понятие простого слоя. Пусть мы имеем две поверхности (о и о7) (рис. 6), расположенные бесконечно близко друг к другу. Обозначим через т объем, заключенный между этими двумя поверхностями. Разобьем объем т на элементарные объемы dr с элементарными массами dm и будем неограниченно приближать поверхность ст' к ст, но при этом оставлять неизменной массу внутри элементарного объема.  В результате масса будет сконденсирована на поверхность о, и этот слой не будет иметь толщины. Такое распределение масс называют простым слоем. Строго говоря, физически простого слоя в природе не существует, но понятие это вводится, так как упрощаются многие математические выкладки в теории потенциала. Формулу для потенциала тяготения простого слоя напишем по аналогии с формулой для потенциала тяготения объемных масс:  Физический смысл потенциала силы тяготения. Потенциал силы тяготения есть работа, которую совершает сила тяготения при перемещении единичной массы из бесконечности в данную точку. Уравнение уровенных поверхностей для потенциала силы тяготения имеет вид Свойства потенциала силы тяготения формулируются следующим образом: Потенциалы тяготения объемных масс (2.15) и простого слоя (2.16) непрерывны, однозначны и конечны во всем пространстве. Вне притягивающих масс потенциалы тяготения имеют непрерывные производные любых порядков. Первые производные потенциала тяготения объемных масс непрерывны во всем пространстве. Первые производные потенциала тяготения простого слоя терпят разрыв при пересечении слоя. Вторые производные потенциала тяготения объемных масс меняются скачком там, где скачком меняется плотность. Потенциал силы тяготения во внешнем пространстве удовлетворяет уравнению Лапласа (2.18), а во внутреннем - уравнению Пуассона (2.19). 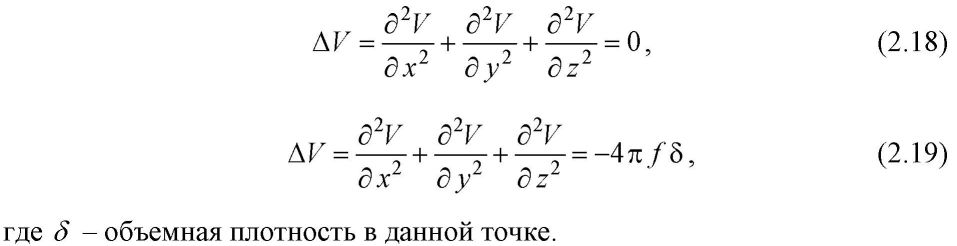 7. На бесконечности потенциалы силы тяготения являются регулярными функциями, то есть удовлетворяют условиям  1.2 Сила тяжести, центробежная сила. Их потенциалы На каждую точку М, находящуюся на земной поверхности, действует 2 силы: сила тяготения F и центробежная сила К, вызванная вращением Земли (рис. 7).    В формулах (2.23) Кх, Kv, Kz - проекции центробежной силы соответственно на оси x,y,z. Потенциал центробежной силы находится по формуле  Формула (2.24) доказывается, исходя из математического выражения для потенциала центробежной силы. Для Земли он равен нулю на полюсе и имеет максимальное значение на экваторе. Оператор Лапласа для потенциала центробежной силы записывается в виде  Потенциал силы тяжести обладает теми же свойствами, что и потенциал силы тяготения. Уравнение Лапласа для внешнего пространства и уравнение Пуассона для внутреннего пространства для потенциала силы тяжести выглядят следующим образом:   1.3. Вторые производные потенциала силы тяжести 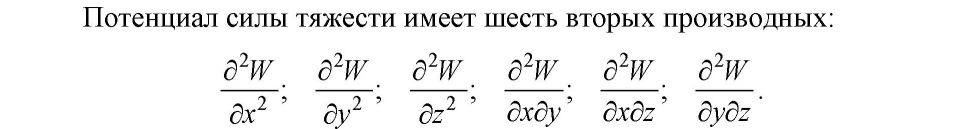 Если ось z направлена по направлению силы тяжести, а оси х и у расположены в плоскости горизонта и имеют направление, соответственно, на север и на восток, то физический смысл вторых производных будет следующим.   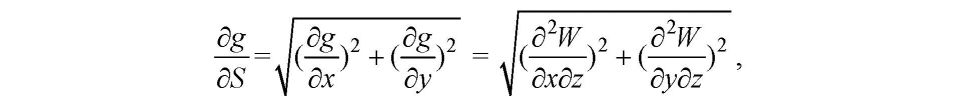 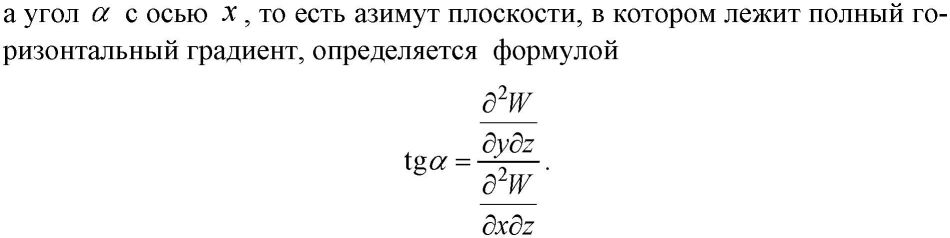  2. Вековые и периодические изменения силы тяжести Земли. Сила тяжести зависит от многих факторов. Она зависит от взаимного расположения Земли и других небесных тел, в основном, Луны и Солнца, от скорости вращения Земли, состояния атмосферы, уровня грунтовых вод, хозяйственной деятельности человека и т.д. Поэтому с течением времени величина и направление силы тяжести изменяются. Эти изменения принято делить на приливные и неприливные. Неприливные изменения силы тяжести, в свою очередь, можно разделить на вековые, периодические и непериодические. Причиной вековых изменений силы тяжести является вековое изменение скорости вращения Земли, а также ряд геофизических факторов, связанных с перемещениями глубинных масс внутри Земли, например, движением литосферных плит. Величины вековых изменений малы и в обычных гравиметрических измерениях не учитываются. Причиной неприливных периодических изменений силы тяжести являются различные метеорологические факторы: годовые и суточные колебания атмосферного давления, сезонные выпадения осадков, колебания уровня грунтовых вод и влажности почвы. Амплитуды этих изменений невелики и составляют менее 10 мкГал. Непериодические вариации силы тяжести обусловлены неравномерностью скорости вращения Земли, землетрясениями и извержениями вулканов, хозяйственной деятельностью человека и т.д. Вызываемые этими явлениями изменения силы тяжести могут быть сравнительно велики. Например, вариации скорости вращения Земли вызывают изменения силы тяжести на 2 - 3 мкГал в месяц. Строительство котлована глубиной 1 м (например, при открытом способе добычи полезных ископаемых) вызовет изменение силы тяжести на границе этого котлована примерно на 0,05 мГал. Колебания уровня воды в водохранилище ГЭС на 25 м вызывают вариации силы тяжести в прибрежной зоне порядка 1,5 - 2,0 мГал. Ясно, что факт изменения силы тяжести во времени необходимо учитывать в геодезических измерениях 3. Аномальное гравитационное поле Земли. Аномалии Буге, аномалии Фая Аномальное гравитационное поле Земли (АГП) характеризует отклонение действительного гравитационного поля Земли (ДГП) от нормального гравитационного поля Земли (НГП). Как известно из предыдущего материала, характеристиками действительного гравитационного поля являются действительная сила тяжести g, действительный потенциал силы тяжести W и вторые производные действительного потенциала силы тяжести W", а характеристиками нормального гравитационного поля, соответственно, - нормальная сила тяжести у, нормальный потенциал силы тяжести U и вторые производные нормального потенциала силы тяжести U” (рис. 9). Указанные характеристики каждого из полей, конечно же, отличаются между собой. В соответствии с этим возникают характеристики аномального гравитационного поля, которые являются ничем иным как различием между соответствующими характеристиками действительного и нормального гравитационных полей.  Разберем эти различия, чтобы четко уяснить характеристики аномального гравитационного поля (ДТП). При этом заметим, что указанные различия обусловлены возмущающими массами, под которыми понимают отступления распределения масс реальной Земли от теоретического распределения масс принятой нормальной Земли. Действительная сила тяжести g отличается от нормальной силы тяжести у по величине и по направлению. Разность величин действительной силы тяжести и нормальной силы тяжести в точке наблюдения называется аномалией силы тяжести. Отклонение направления действительной силы тяжести от направления нормальной силы тяжести приводит к понятию уклонения отвеса. Согласно приведенному определению выражение для аномалии силы тяжести в общем случае имеет вид В зависимости от того, какие возмущающие массы вызвали отклонения g от у, различают несколько видов аномалий силы тяжести, которые могут быть: аномалиями в свободном воздухе; топографическими аномалиями; аномалиями Буге; аномалиями Фая; аномалиями Прея. Математически это выражается различными поправками за конкретные возмущающие массы, введенными в формуле (2.49) в действительную силу тяжести, и поправкой за высоту в нормальную силу тяжести. Кроме того, все перечисленные аномалии силы тяжести могут быть смешанными и чистыми. Чистые аномалии силы тяжести образуются в том случае, если g и у относятся к одной точке пространства. Если же g и у отнесены к разным точкам пространства, то возникают смешанные аномалии силы тяжести, с которыми чаще всего мы и имеем дело на практике. Приступим к рассмотрению основных видов аномалий силы тяжести. Аномалии в свободном воздухе учитывают все возмущающие массы, которые расположены как на поверхности Земли, так и внутри нее, то есть в этом случае никакой поправки в измеренное значение действительной силы тяжести не вводится, а учитывается только поправка за редуцирование нормальной силы тяжести с поверхности эллипсоида на поверхность Земли (поправка за высоту). 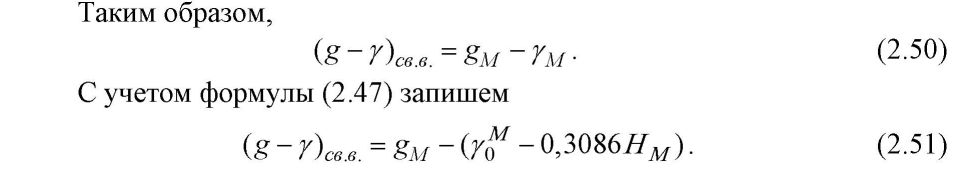 Формулы (2.50) и (2.51) определяют чистую аномалию в свободном воздухе. Обозначения для этих формул даны на рис. 10. Однако на практике обычно работают в системе нормальных высот. Нормальная высота дает расстояние от поверхности геоида (квазигеоида) до земной поверхности (рис. 10). Поэтому нормальные высоты всегда несколько меньше геодезических. Если мы нормальную высоту отложим от поверхности эллипсоида, то получим точку N. Подставив в формулу (2.51) вместо геодезической нормальную высоту, получим смешанную аномалию силы тяжести в свободном воздухе  Топографическая аномалия силы тяжести возникает в том случае, когда из аномалии в свободном воздухе убирается эффект возмущающих масс топографического слоя, то есть масс, расположенных между уровнем моря и физической поверхностью Земли (рис. 11).    Так как вычисление поправки за топографический слой производится по сложной формуле (2.55), то на практике вместо топографической аномалии часто используют более простую для вычислений аномалию Буге. При вычислении аномалии Буге топографический слой принимают за плоский слой бесконечного простирания, проведенный на высоте точки наблюдения (рис. 12). 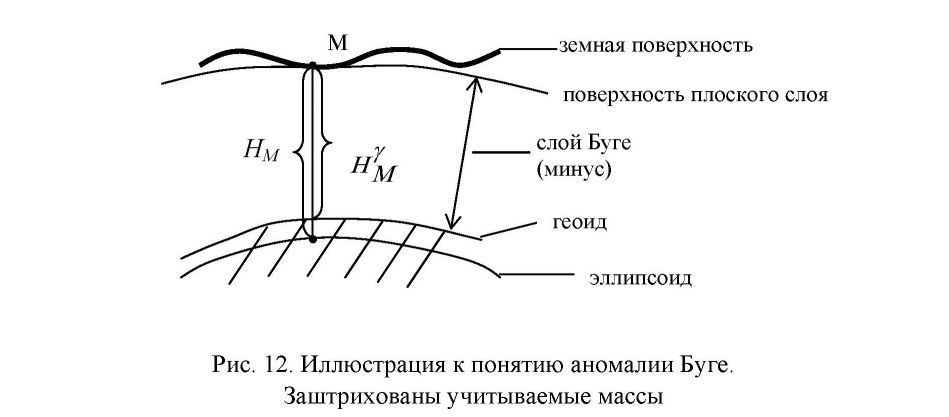 В этом случае в значение действительной силы тяжести вводится поправка Буге, и выражение для вычисления аномалии Буге получится следующим:  Если в формуле (2.56) Н- геодезическая высота, то получаем чистую аномалию Буге, если нормальная - смешанную аномалию Буге. Отметим, что выражение (2.56) справедливо только для равнинных районов. В горных районах при вычислении аномалии Буге учитывают еще поправку за рельеф на высоте точки наблюдения, то есть на уровне этой высоты рельеф как бы выравнивают (рис. 13).   Рассмотренные виды аномалии силы тяжести применяются в зависимости от поставленных задач. Так геодезистов чаще всего интересуют аномалии в свободном воздухе, геологов - аномалии Буге. Геодезисты используют также аномалии Буге и топографические аномалии для косвенного интерполирования аномалий силы тяжести. Вопрос косвенного интерно- лирования мы разберем несколько позднее, а сейчас рассмотрим оставшиеся характеристики аномального гравитационного поля, показанные на рис. 9.  Уклонения отвеса характеризуют отличия направления действительной силы тяжести от направления нормальной силы тяжести и от направления нормали к эллипсоиду (рис. 15). Существует два вида уклонения отвеса: гравиметрическое (абсолютное) и астрономо-геодезическое (относительное). Угол между направлением нормальной силы тяжести и направлением действительной силы тяжести есть гравиметрическое уклонение отвеса:  Угол между направлением действительной силы тяжести и направлением нормали к эллипсоиду есть астрономо-геодезическое уклонение отвеса: На практике чаще всего используют не полные значения уклонений отвеса и, а их составляющие в меридиане и в первом вертикале, то есть проекции угла и на плоскость меридиана и на плоскость первого вертикала г]. Эти проекции связаны с полными уклонениями отвеса следующим образом: 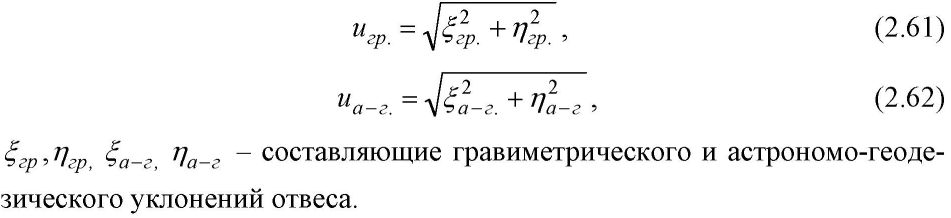 Формулы перехода от составляющих гравиметрических уклонений отвеса к составляющим астрономо-геодезических уклонений отвеса имеют вид   Из рис. 16 также следует второе определение аномалии высоты как высоты поверхности квазигеоида над поверхностью эллипсоида. Понятие квазигеоид (почти геоид) введено Молоденским. Поверхность квазигеоида получается путем отложения нормальной высоты вниз от земной поверхности. Геодезические и нормальные высоты связаны с потенциалами силы тяжести выражениями 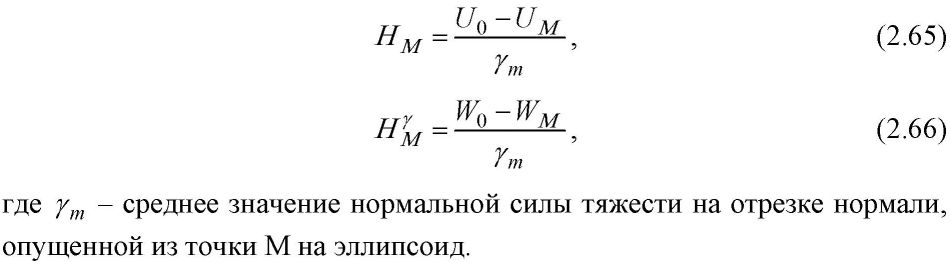 Возмущающий потенциал Т определяется как разность между действительным потенциалом силы тяжести W и нормальным потенциалом силы тяжести U: Возмущающий потенциал является важнейшей характеристикой аномального гравитационного поля. К его определению сводится задача определения гравитационного поля Земли (задача Стокса и задача Моло- денского). |
