|
|
ИДЗ_0a43. Группа оа4
Тема – Механика
Вариант 7
Две дороги пересекаются под углом 60 . От перекрестка по ним удаляются машины. Одна – со скоростью 60 км/ч. Другая 80 км/ч. Определить скорости удаления одной машины относительно другой. Перекресток машины прошли одновременно.
Поезд движется по закруглению радиусом 500 м. Ширина железнодорожной колеи 152,4 см. Наружный рельс расположен на 12 см выше внутреннего. При какой скорости движения поезда на закруглении колеса не оказывают давления на рельсы?
Гладкая упругая нить длины lи жесткости k подвешена одним концом к точке О. На нижнем конце имеется невесомый упор. Из точки О начала падать небольшая муфта массы m. Найти: а) максимальное растяжение нити; б) убыль механической энергии системы к моменту установления равновесия (из-за сопротивления воздуха).
Космонавт массой m1 приближается к космическому кораблю массой m2 с помощью легкого троса. Первоначально корабль и космонавт неподвижны, а расстояние между ними равно l. Какое расстояние пройдут корабль и космонавт до встречи?
Космический корабль движется по круговой орбите радиусом R вокруг Земли со скоростью v, вдвое большей скорости свободного движения по той же орбите. Какую силу тяги развивают двигатели корабля, если его масса m?
Имеются две одинаковые шайбы А и Б. Шайба А лежит неподвижно на абсолютно гладкой поверхности, а шайба Б движется поступательно и вращается с угловой скоростью Б = 2 рад/с. Определить угловую скорость вращения системы из двух шайб после соударения, если удар был центральным и абсолютно неупругим.
Горизонтально расположенный гладкий стержень АВ вращают с угловой скоростью = 2 рад/с вокруг вертикальной оси, проходящей через его конец А. По стержню свободно скользит муфточка массой m = 0,5 кг, движущаяся из точки А с некоторой начальной скоростью. В тот момент, когда муфточка находится на расстоянии r = 50 см от оси вращения, на нее действует сила Кориолиса, равная 3 Н. Найти начальную скорость муфточки.
В К-системе отсчета мю-мезон, движущийся со скоростью v = 0,99 с, пролетел от места рождения до точки распада расстояние l = 3 км. Определить: 1) собственное время жизни мезона; 2) расстояние, которое пролетел мезон в К-системе с «его точки зрения».
Тема – Механика
Вариант 8
Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени дается уравнением S = Ct3. Здесь: С = 0,1 см/с3. Найти нормальное и тангенциальное ускорения точки в момент времени, когда её линейная скорость равна 0,3 м/с.
С какой скоростью движется конькобежец по закруглению ледяной дорожки радиусом 10 м, если, проходя этот поворот, он наклоняется к горизонту под углом 76 ?
Потенциальная энергия частицы в некотором поле имеет вид U = a/r2 – b/r, где а и b – положительные постоянные; r – расстояние от центра поля. Найти: а) значение r0, соответствующее равновесному положению частицы; выяснить, устойчиво ли это положение; б) максимальное значение силы притяжения; изобразить примерные графики зависимостей U(r) и Fr(r)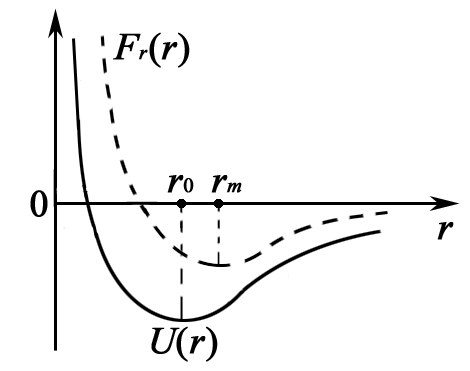
Водомерный двигатель катера забирает воду из реки и выбрасывает ее со скоростью u = 10,0 м/с относительно катера назад. Масса катера М = 1000 кг. Масса ежесекундно выбрасываемой воды постоянна и равна m = 10,0 кг/с. Пренебрегая сопротивлением движению катера, определить: а) скорость катера vспустя время t= 1,00 мин после начала движения; б) какой предельной скорости vmax может достичь катер.
Для осуществления всемирной телевизионной связи достаточно иметь три спутника Земли, вращающихся по круговой орбите в плоскости экватора с запада на восток и расположенных друг относительно друга под углом 120 . Период обращения каждого спутника Т = 24ч. Определить радиус орбиты и линейную скорость такого спутника.
Сплошной однородный диск радиусом R = 10 см, имеющий начальную угловую скорость 0 = 50 рад/с (относительно оси, перпендикулярной к плоскости диска и проходящей через центр масс), кладут на горизонтальную поверхность. Сколько оборотов сделает диск до остановки, если коэффициент трения между поверхностью и диском = 101 и не зависит от угловой скорости вращения диска? Рекомендации. Примите метод дифференцирования и интегрирования.
Самолет летает на постоянной высоте по окружности радиуса R с постоянной скоростью v. В кабине самолета установлены пружинные и маятниковые часы. Какое время полета t покажут маятниковые часы, если это время, измеренное пружинными часами, равно t. Силу Кориолиса, ввиду ее малости, не учитывать.
Пара протон – антипротон может образоваться при соударении протона с кинетической энергией К 6 ГэВ с неподвижным протоном. Найти, каковы должны быть наименьшие одинаковые энергии встречных протонных пучков для осуществления этой реакции.
Тема – Механика
Вариант 9
Два тела движутся взаимно перпендикулярными курсами соответственно со скоростями v1 = 6 м/с и v2 = 8 м/с. Чему равна величина скорости первого тела относительно второго? 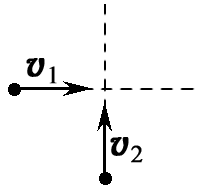
Определите силы натяжения нитей, связывающих грузы в системе, изображенной на рисунке. Массы тел соответственно m1 = 1 кг; m2 = 2 кг; m3 = 4 кг. Коэффициент трения первого тела о наклонную плоскость 1 = 0,1, коэффициент трения второго тела о наклонную плоскость 2 = 0,2. Угол наклона плоскости к горизонту = 30 . (Трением в блоке пренебрегаем).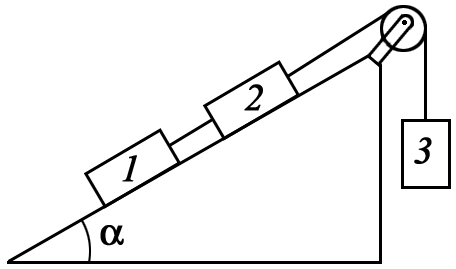
Боек автоматического молота массой 100 кг падает на заготовку детали, масса которой вместе с наковальней 2000 кг. Скорость молота в момент удара 2 м/с. Считая удар абсолютно неупругим, определить энергию, идущую на деформацию заготовки.
Частица массой m испытала столкновение с покоившейся частицей массой M, в результате которого частица m отклонилась на угол /2, а частица М отскочила под углом = 30 к первоначальному направлению частицы m. На сколько процентов и как изменилась кинетическая энергия этой системы после столкновения, если М/m = 5,0?
Двойная звезда – это система из двух звезд, движущихся вокруг общего центра масс. Расстояние l между компонентами двойной звезды и период Т ее вращения известны. Считая, чтоlне меняется, определите суммарную массу двойной звезды.
В лаборатории для исследования магнитных полей используют магнитную стрелку на подставке. Муха, летящая на запад, села на конец стрелки. Определить начальную угловую скорость, приобретенную стрелкой после посадки. Принять: массу стрелки М = 20 г; длину стрелки l = 7 см; массу мухи m = 5 г; скорость полета v = 5 м/с.
Горизонтально расположенный стержень вращается вокруг вертикальной оси, проходящей через его конец, с угловой скоростью = 1,00 рад/с. Расстояние от оси до конца стержня l = 1 м. На стержень надета муфта массой m = 0,1 кг. Муфта закреплена с помощью нити на расстоянии l0 = 0,1 м от оси вращения. В момент t = 0 нить пережигают, и муфта начинает скользить по стержню практически без трения. Найти: а) время , спустя которое муфта слетит со стержня; б) силу F, с которой стержень действует на муфту в момент ; в) работу А, которая совершается над муфтой за время в неподвижной системе отсчета.
Мощность излучения Солнца 41026 Вт. На сколько уменьшается ежесекундно масса Солнца? С каким ускорением двигалось бы Солнце и какую скорость оно приобрело бы за 1 год ( 3107 с), если бы весь свет испускался только в одном направлении (фотонный двигатель)?
Тема – Механика
Вариант 10
Мяч, брошенный со скоростью 10 м/с под углом 60 к горизонту, ударяется о стену, находящуюся на расстоянии 3 м от места бросания. Определите модуль скорости мяча после удара о стенку. Удары считайте абсолютно упругими.
Тело массой m = 3 кг брошено под углом = 60 к горизонту с начальной скоростью v = 20 м/с. Определите, на сколько изменился импульс тела в верхней точке траектории по сравнению с начальным импульсом Р0 = mv0.
Легкий пластмассовый шарик для игры в настольный теннис роняют с высоты h. В нижней точке его траектории по нему ударяют ракеткой снизу вверх, после чего шарик подпрыгивает на высоту, в n раз большую первоначальной. Определить скорость ракетки в момент удара. Считать удар упругим, сопротивлением воздуха пренебречь. Масса ракетки много больше массы шарика.
Веревка привязана к санкам и переброшена через перекладину ворот высотой h. Мальчик, сидящий на санках, начинает выбирать веревку, натягивая ее с силой Т. Какую скорость он приобретет, проезжая под перекладиной? Начальная длина веревки 2l, масса мальчика с санками m. Трением пренебречь.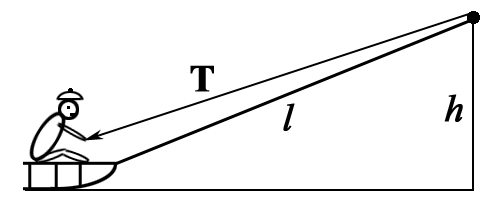
Какую минимальную работу нужно совершить, чтобы переместить тело массой m с поверхности Луны на Землю? Считать, что в процессе движения взаимное расстояние Н между Луной и Землей не меняется.
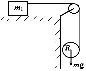 Система состоит из груза m1 = 1 кг, невесомого блока и сплошного цилиндра массой m2 = 10 кг и радиусом R = 10 см (см. рисунок). Груз m1 движется по горизонтальной плоскости без трения. Одновременно с цилиндра сматывается шнур. Определите: а) ускорение центра масс цилиндра; б) ускорение груза m1; в) силу натяжения нити; г) угловое ускорение цилиндра. Система состоит из груза m1 = 1 кг, невесомого блока и сплошного цилиндра массой m2 = 10 кг и радиусом R = 10 см (см. рисунок). Груз m1 движется по горизонтальной плоскости без трения. Одновременно с цилиндра сматывается шнур. Определите: а) ускорение центра масс цилиндра; б) ускорение груза m1; в) силу натяжения нити; г) угловое ускорение цилиндра.
Через невесомый блок перекинута веревка с грузами массой m и М. Блок движется вверх с ускорением а. Пренебрегая трением на блоке, найти давление блока на ось, силу натяжения веревки и ускорения грузов.
Какую работу необходимо совершить, чтобы увеличить скорость частицы с массой покоя m0 от 0,6 до 0,8 с? Сравним полученный результат со значением, вычисленным по нерелятивистской формуле.
Тема – Механика
Вариант 11
Двое играют в мяч. От одного к другому мяч летит 2 с. Определить максимальную высоту подъема мяча.
Определите силу натяжения нити в системе тел, изображенной на рисунке, где m1 = 2 кг; m2 = 3 кг; m3 = 5 кг. Коэффициент трения между телами 1 и 2 = 0,2. Угол наклона плоскости к горизонту = 45. (Трением между телом 2 и наклонной плоскостью, а также трением в блоке пренебрегаем).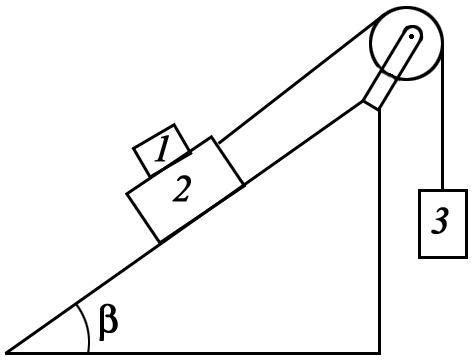
Брусок массы m = 1,00 кг находится на горизонтальной плоскости с коэффициентом трения = 0,27. В некоторый момент ему сообщили начальную скорость v0 = 1,50 м/с. Найти среднюю мощность силы трения за все время движения бруска.
Замкнутая система состоит из двух одинаковых частиц, которые движутся со скоростями v1 и v2 так, что угол между направлениями их движения равен . После упругого столкновения скорости частиц оказались равными v1 и v2. Найти угол между направлениями их разлета.
Два однородных шара радиусами R1 и R2 соприкасаются друг с другом. Как изменится потенциальная энергия гравитационного взаимодействия этих шаров, если радиус каждого шара увеличить в 2 раза, не нарушая при этом соприкосновение шаров?
Флюгер в виде однородного стержня может вращаться вокруг вертикальной оси, проходящей через центр симметрии. Масса флюгера М = 100 г, а длина l = 20 см. Мальчик выстрелил в него из рогатки кусочком жвачки массой m = 30 г. Жвачка летела под углом = 30 к линии флюгера в плоскости вращения последнего, и, попав в его конец, прилипла. При этом флюгер приобрел начальную угловую скорость = 2 рад/с. Определить жесткость резины рогатки, если мальчик растянул ее на х = 10 см. (Учесть, что у рогатки две резинки).
Стержень ОА вращается относительно вертикальной оси ОВ с угловой скоростью . Угол между осью и стержнем . По стержню без трения скользит муфта массой М, связанная с точкой О пружиной жесткостью k. В недеформированном состоянии диска длина пружины l0. Определить положение муфты при вращении.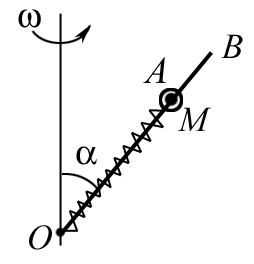
Стержень, собственная длина которого равна l0, покоится в системе отсчета К: он расположен так, что составляет с осью х угол . Какой угол составляет этот стержень с осью х другой системы отсчета К? Чему равна длина этого стержня в системе К?
Тема – Механика
Вариант 12
С высоты 2 м вниз под углом к горизонту 60 брошен мяч с начальной скоростью 8,7 м/с. Определите расстояние между двумя последовательными ударами мяча о землю. Удары считать абсолютно упругими.
Мотоциклист на мотоцикле участвует в гонках по вертикали и едет по внутренней поверхности вертикального цилиндра радиусом R= 15 м, при этом центр тяжести мотоцикла с человеком расположен на расстоянии d = 75 см от поверхности цилиндра. Угол наклона мотоциклиста к плоскости горизонта составляет 30 . Чему равен коэффициент трения покрышек колес мотоцикла о поверхность цилиндра? С какой минимальной скоростью vmin должен ехать мотоциклист, чтобы не сорваться со стены?
Небольшому телу массой m, находящемуся на горизонтальной плоскости, сообщили скорость v0. Коэффициент трения зависит от пройденного пути s по закону = s, где постоянная. Найти максимальную мгновенную мощность силы.
К небольшому бруску массой m = 50 г, лежащему на горизонтальной плоскости, приложили постоянную горизонтальную силу F = 0,10 Н. Найти работу сил трения за время движения бруска, если коэффициент трения зависит от пройденного пути х как = х, где постоянная.
Найти выражение для напряженности поля и силы гравитационного взаимодействия между тонким однородным кольцом радиусом Rи массой М и материальной точкой массой т,лежащей на высоте hна перпендикуляре, восставленном из центра кольца к его плоскости.
Два горизонтально расположенных диска вращаются вокруг общей оси. Ось проходит через их центры. Моменты инерции дисков относительно этой оси равны: J1 = 5 кгм2, J1 = 10 кгм2, а угловые скорости: 1 = 2 с1 и 2 = с1. После падения верхнего диска на нижний, благодаря трению между ними, оба диска через некоторое время начинают вращаться как одно целое. Найти общую угловую скорость системы из двух дисков и работу, которую совершили силы трения.
В системе отсчета, вращающейся вокруг неподвижной оси с = 5,0 рад/с, движется небольшое тело массой m = 100 г. Какую работу совершила центробежная сила инерции при перемещении этого тела по произвольному пути из точки 1 в точку 2, которые расположены на расстояниях r1 = 30 см и r2 = 50 см от оси вращения?
Показать, что выражение релятивистского импульса через кинетическую энергию  при v << с переходит в соответствующее выражение классической механики. при v << с переходит в соответствующее выражение классической механики.
Тема – Механика
Вариант 13
Тело брошено со скоростью v под углом к горизонту. Максимальная высота подъема тела h = 3 м и радиус кривизны траектории в верхней точке траектории R = 3 м. Найти v и .
На наклонной плоскости, угол наклона которой к горизонту составляет 30, лежит тело массой 1 кг. Коэффициент трения тела о плоскость = 0,5. Определите силу трения, действующую на тело. Определите зависимость силы трения, действующей на тело, от угла наклона плоскости к горизонту.
Пуля, летевшая горизонтально со скоростью v = 400 м/с, попадет в брусок, подвешенный на нити длиной l = 4 м, и застревает в нем. Определить угол , на который отклонится брусок, если масса пули m1 = 20 г и масса бруска m2 = 5 кг.
С какой по величине и направлению скоростью должен прыгнуть человек массой m, стоящий на краю тележки массой М и длиной l, чтобы попасть на другой конец к моменту остановки тележки. Коэффициент трения тележки о землю равен .
Два одинаковых однородных шара, изготовленных из одинакового материала, соприкасаются друг с другом. Как изменится сила гравитационного притяжения этих шаров, если массу каждого шара увеличить в 5 раз за счет увеличения их размеров, не нарушая при этом соприкосновение шаров?
Обруч и сплошной цилиндр поднимаются вверх по наклонной плоскости и достигают одинаковой высоты подъема. Определить отношение их линейных скоростей в начале подъема.
Через блок, укрепленный на краю гладкого стола, перекинута веревка, соединяющая грузы с массой m и М. Стол движется вниз с ускорением а. Найти ускорение груза m. Трением и массой блока пренебречь. 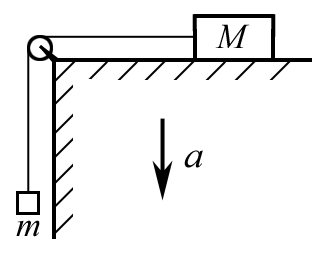
Две нестабильные частицы движутся в К-системе отсчета по некоторой прямой в одном направлении с одинаковой скоростью v = 0,99 с. Расстояние между частицами в этой системе отсчета l = 12 м. В некоторый момент обе частицы распались одновременно в К-системе отсчета, связанной с ним. Найти: 1) промежуток времени между моментами распада обеих частиц в исходной К-системе; 2) какая частица распалась позже в К-системе.
|
|
|
 Скачать 434.58 Kb.
Скачать 434.58 Kb.