Х1 и x3, на которую не накладываются ограничения по знаку, разностью неотрицательных переменных x3
 Скачать 173.99 Kb. Скачать 173.99 Kb.
|
1 2 Три завода А, В и С экспортируют в некоторые страны бесшовные трубы. Из-за низких цен на свою продукцию эти заводы обвиняются в демпинге. Поэтому утверждены объёмы квот в год для каждого завода на производство бесшовных труб на экспорт. Основная часть квоты выделена заводу А – 19500 т. Экспортные квоты на поставку 7500 т и 3000 т труб получили также заводы В и С соответственно. Следовательно, каждый завод не должен экспортировать большее количество труб, чем утверждено, для избежания антидемпинговых процедур. Стоимость перевозки 1 т бесшовных труб и объём потребностей в этих трубах каждой страной, куда экспортируются последние, представлены в таблице: 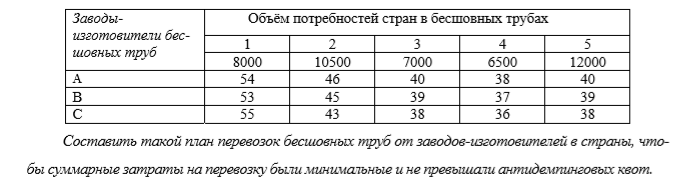 1. Преобразовать следующие задачи линейного программирования в каноническую форму 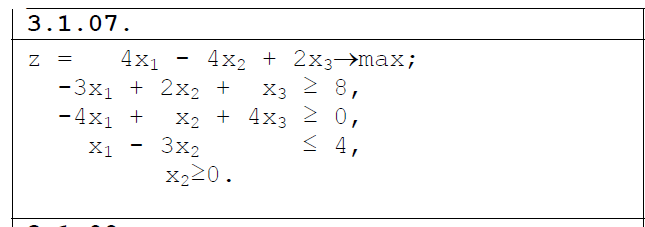 Заменяем переменную х1 и x3, на которую не накладываются ограничения по знаку, разностью неотрицательных переменных x3′ и x3′′, то есть x1 = x4 - x5, x3 = x6 - x7 -3(x4 - x5)+2x2+(x6 - x7)≥8 -4(x4 - x5)+x2+4(x6 - x7)≥0 (x4 - x5)-3x2≤4 z= -4x2+4x4-4x5+2x6-2x7 → max при ограничениях: 2x2-3x4+3x5+x6-x7≥8 x2-4x4+4x5+4x6-4x7≥0 -3x2+x4-x5≤4 Упростим выражение 2x1-3x2+3x3+x4-x5≥8 x1-4x2+4x3+4x4-4x5≥0 -3x1+x2-x3≤4 z= -4x1+4x2-4x3+2x4-2x5 → max В 1-м неравенстве смысла вводим базисную переменную x6 со знаком минус. В 2-м неравенстве смысла вводим базисную переменную x7 со знаком минус. В 3-м неравенстве смысла вводим базисную переменную x8. 2x1-3x2+3x3+x4-x5-x6 = 8 x1-4x2+4x3+4x4-4x5-x7 = 0 -3x1+x2-x3+x8 = 4 2. Преобразовать следующие задачи линейного программирования в стандартную форму. 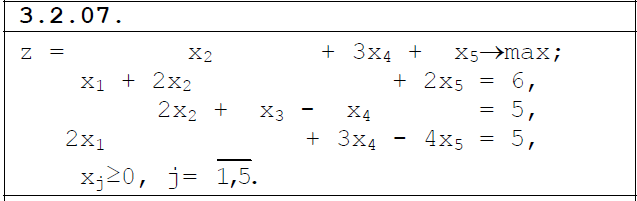 Данное преобразование будем проводить с помощью метода Жордана- Гаусса, выделяя в каждом уравнении базисную переменную. Исходную систему линейных уравнений перед преобразованием удобно записать в виде матрицы или таблицы: 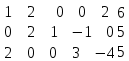 вычитаем из строчки 3 строчку , которая умноженная на 2 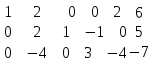 строку 2 делим на 2 строку 2 делим на 2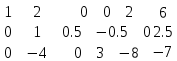 вычитаем из строчки 3 строчку 2, которая умноженная на -4 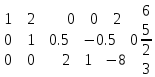 строку 3 делим на строчку 2 строку 3 делим на строчку 2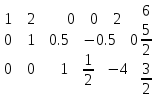 вычитаем из строчки 2 строчку 3, которая умноженная на 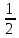 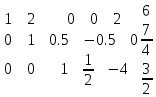 вычитаем из строчки 1 строчку 2, которая умноженная на 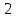 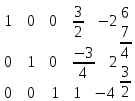 Вернёмся к первоначальной форме записи. 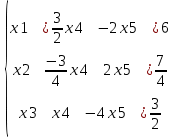 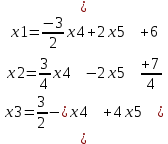 Учитывая, что х1 ≥ 0, х2 ≥ 0, х3 ≥ 0 из (3.10) получаем: 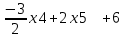 ≥ 0 ≥ 0 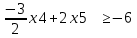 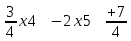 ≥ 0 ≥ 0 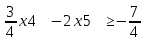 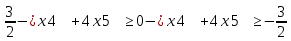 Далее в целевую функцию z подставляем выражения х1,х2 и x3 из , получаем Z = 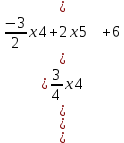 + + 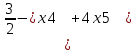 - x4 + 4x5 = - x4 + 4x5 = 1 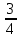 x4 + 8x5 + 9 x4 + 8x5 + 9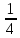 Таким образом, получаем следующую задачу линейного программирования в стандартной форме Z= 1 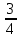 x4 + 8x5 + 9 x4 + 8x5 + 9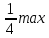 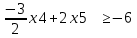 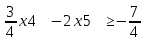 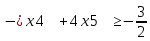 1. Решить следующие задачи линейного программирования графическим методом. 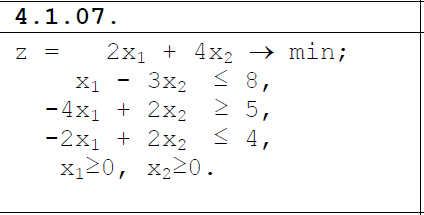 Задача находится в стандартной форме и имеет две переменные и, следовательно, может быть решена графическим методом. Строим ОДЗ для переменных задачи. x1- 3x2 = 8 x1=0 - x1= 0 x2= -8 - x2 = -8/3 По этим двум точкам строим прямую. Определяем, какая из полуплоскостей является решением данного неравенства. Для этого подставляем координаты любой точки, не принадлежащей прямой, в первое неравенство. Для простоты вычислений возьмём точку (0;0). Получим 0 *0 -3 ≤ 8 Такое неравенство является истинным и, следовательно, полуплоскость, на которой расположена точка (0;0), является искомой. 2. Решить следующие задачи линейного программирования графическим методом, предварительно преобразовав их к стандартному виду. 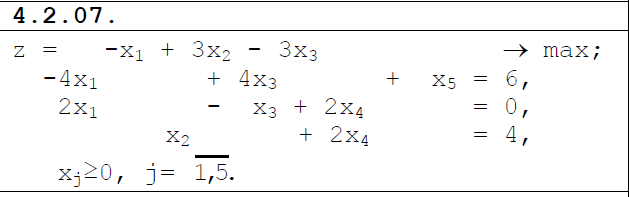 Данное преобразование будем проводить с помощью метода Жордана- Гаусса, выделяя в каждом уравнении базисную переменную. Исходную систему линейных уравнений перед преобразованием удобно записать в виде матрицы или таблицы: Матричный вид записи: Ax=b, где Первый этап. Прямой ход Гаусса. Исключим элементы 1-го столбца матрицы ниже элемента a1,1. Для этого сложим строку 2 со строкой 1, умноженной на 1/2:
Ведущий элемент a2 2=0. Следовательно, для продолжения процедуры нужно выбирать ненулевой ведущий элемент посредством перестановки строк . Для этого выбираем самый большой по модулю ведущий элемент столбца 2 ниже элемента a2 2 и меняем местами строки 2 и 3.
Второй этап. Обратный ход Гаусса. Исключим элементы 3-го столбца матрицы выше элемента a3,3. Для этого сложим строку 1 со строкой 3, умноженной на -4/4:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Из расширенной матрицы восстановим систему линейных уравнений:
1 2 |
