Х1 и x3, на которую не накладываются ограничения по знаку, разностью неотрицательных переменных x3

Название	Х1 и x3, на которую не накладываются ограничения по знаку, разностью неотрицательных переменных x3
Дата	13.01.2021
Размер	173.99 Kb.
Формат файла
Имя файла	matemt_programm.docx
Тип	Документы #167807
страница	2 из 2

1 2

x₁

x₂

x₃

x₄

−

x₅

−

x₁

x₂

x₃

x₄

x₅

x₁

x₂

x₃

x₄

x₅

Базисные переменные x1, x2, x3, свободные переменные x4, x5.

Выразив базисные переменные x1, x2, x3 через свободные, получим решение:

x₁=

−

x₅

x₂=

−2

x₄

x₃=

−

x₅

5.1. Решить следующие задачи линейного программирования симплекс-методом.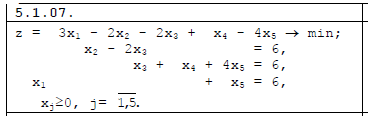

Приведём исходную задачу к канонической форме.

Преобразуем неравенства в равенства добавлением неотрицательных переменных:

3 x1−2 x2−2 x3+1 x4−4 x5+0 x6+0 x7+0 x8→ min

x1,x2,x3,x4,x5,x6,x7,x8 ≥0

Матрица коэффициентов A=ǁaijǁ системы уравнений имеет вид:

0	1	-2	0	0	1	0	0
0	0	1	1	4	0	1	0
1	0	0	0	1	0	0	1

Правая часть ограничений системы уравнений B имеет вид:

Целевая функция C имеет вид:

-2

-4

Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка - это целевая функция

1 Таб.

Б	Ао	А1	А2	A3	A4	A5	A6	A7	A8
A2	6	0	1	-2	0	0	1	0	0
A4	6	0	1	1	1	4	0	1	0
A1	6	1	0	0	0	1	0	0	1
Z’j-сj	0	3	-2	-2	1	-4	0	0	0

Базисные векторы x₂, x₄, x₁, следовательно, все элементы в столбцах x₂, x₄, x₁, ниже горизонтальной линии должны быть нулевыми.

Обнулим все элементы столбца x2, кроме ведущего элемента. Для этого сложим строку 4 со строкой 1, умноженной на 2. Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 4 со строкой 2, умноженной на -1. Обнулим все элементы столбца x1, кроме ведущего элемента. Для этого сложим строку 4 со строкой 3, умноженной на -3.

Симплекс таблица примет вид:

Б	Ао	А1	А2	A3	A4	A5	A6	A7	A8
A2	6	0	1	-2	0	0	1	0	0
A4	6	0	0	1	1	4	0	1	0
A1	6	1	0	0	0	1	0	0	1
Z’j-сj	6	0	0	-7	0	-3	2	-1	-3

Шаг 1

Запишем текущий опорный план:

X=( 0 6 0 6 0 0 0 0)

Значение целевой функции в данной точке:

Z=3⋅0−2⋅6−2⋅0+1⋅6+4⋅0+0⋅0+0⋅0+0⋅0=−6

Данный опорный план не является оптимальным, так как на пересечении строки 4 и столбцов x1, x2, x3, x4, x5, x6, x7, x8 есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-7), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем min (ai,0 /ai,3), при ai,3>0, i=1,...3. min(6:1)=6 соответствует строке 2. Из базиса выходит вектор x4. Сделаем исключение Гаусса для столбца x3, учитывая, что ведущий элемент соответствует строке 2. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки 1, 4 со строкой 2, умноженной на 2, 7, соответственно.

Симплекс таблица примет следующий вид:

Б	Ао	А1	А2	A3	A4	A5	A6	A7	A8
A2	18	0	1	0	2	8	1	2	0
A3	6	0	0	1	1	4	0	1	0
A1	0	1	0	0	0	1	0	0	1
Z’j-сj	48	0	0	0	7	25	2	6	-3

Шаг 2

Запишем текущий опорный план:

X=(0 1 8 6 0 0 0 0 0)

Значение целевой функции в данной точке:

Z=3⋅0−2⋅18−2⋅6+1⋅0+4⋅0+0⋅0+0⋅0+0⋅0=−48 Z=C⋅X=3⋅0−2⋅18−2⋅6+1⋅0+4⋅0+0⋅0+0⋅0+0⋅0=−48

Данный опорный план не является оптимальным, так как на пересечении строки 4 и столбцов x1, x2, x3, x4, x5, x6, x7, x8 есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор x8. Определяем, какой вектор выходит из базиса. Для этого вычисляем min(ai,0 /ai,8), при ai,8>0, i=1,...3. min(0:1)=0 соответствует строке 3. Из базиса выходит вектор x1. Сделаем исключение Гаусса для столбца x8, учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строку 4 со строкой 3, умноженной на 3

Симплекс таблица примет следующий вид:

Б	Ао	А1	А2	A3	A4	A5	A6	A7	A8
A2	18	0	1	0	2	8	1	2	0
A3	6	0	0	1	1	4	0	1	0
A8	0	1	0	0	0	1	0	0	1
Z’j-сj	48	3	0	0	7	28	2	6	0

Шаг 3

Запишем текущий опорный план:

X=(0 1 8 6 0 0 0 0 0)

Значение целевой функции в данной точке:

F=C⋅X=3⋅0−2⋅18−2⋅6+1⋅0+4⋅0+0⋅0+0⋅0+0⋅0=−48 Z=C⋅X=3⋅0−2⋅18−2⋅6+1⋅0+4⋅0+0⋅0+0⋅0+0⋅0=−48

Текущий опорный план является оптимальным, так как в последней строке нет отрицательных элементов.

Решение канонической задачи можно записать так:

X∗0=(0 1 8 6 0 0 0 0 0)

Решение исходной задачи:

Xmax=(0 1 8 6 0 0)

или

x1=0,x2=18,x3=6,x4=0,x5=0x1=0,x2=18,x3=6,x4=0,x5=0

Значение целевой функции в оптимальной точке:

Zmax=3⋅0−2⋅18−2⋅6+1⋅0+4⋅0=−48

Ответ: Xmax=(0 1 8 6 0 0) Zmax −48

5.2. Решить следующие задачи линейного программирования симплекс-

методом.

Нахождение оптимального плана задачи линейного программирования симплекс методом:

4 x1+3 x2→ min

x1− x2≤30

x1+3 x2≥0

x1,x2 ≥0

Преобразуем неравенства в равенства добавлением неотрицательных переменных:

4 x1+3 x2+0 x3+0 x4→ min

x1−x2+ x3 =30

3 x2- x4=0

x1,x2,x3,x4 ≥0

Так как количество базисных векторов должен быть 2, то добавляем искусственные переменные, а в целевую функцию добавляем эти переменные, умноженные на M, где M, очень большое число:

4x1+3x2+0+M x5→ min

{x1− x2+x3=30

{3 x2-x4+x5=0

x1,x2,x3,x4,x5 ≥0

Матрица коэффициентов A=ǁaijǁ системы уравнений имеет вид:

1	-1	1	0	0
0	3	0	-1	1

Правая часть ограничений системы уравнений B имеет вид:

Целевая функция C имеет вид

Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, разделенная на две части. Последняя строка − строка с исскуственными переменными:

Базис	X0	X1	x2	x3	x4	x5
x1	3	1	-1	1	0	0
x2	0	0	3	0	-1	1
Z’j-сj	0	4	3	0	0	0
Z’j-сj	0	0	0	0	0	1

Базисные векторы x1, x5, следовательно, все элементы в столбцах x1, x5, ниже горизонтальной линии должны быть нулевыми.

Обнулим все элементы столбца x1, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на -4. Обнулим все элементы столбца x5, кроме ведущего элемента. Для этого сложим строку 4 со строкой 2, умноженной на -1.

Симплекс таблица примет вид:

Базис	X0	X1	x2	x3	x4	x5
x1	3	1	-1	1	0	0
X2	0	0	3	0	-1	1
Z’j-сj	-12	0	7	-4	0	0
Z’j-сj	0	0	-3	0	1	0

Шаг 1

Запишем текущий опорный план:

X=(30000)X=(30000)

Значение целевой функции в данной точке:

Z=C⋅X=4⋅3+3⋅0+0⋅0+0⋅0+M⋅0=12

Данный опорный план не является оптимальным, так как на пересечении строки 4 и столбцов x1, x2, x3, x4 есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем min(ai,0 /ai,2), при ai,2>0, i=1,...2. min(0:3)=0 соответствует строке 2. Из базиса выходит вектор x5. Сделаем исключение Гаусса для столбца x2, учитывая, что ведущий элемент соответствует строке 2. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки 1, 3, 4 со строкой 2, умноженной на 1/3, -7/3, 1, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.

Симплекс таблица примет следующий вид:

Базис	X0	X1	x2	x3	x4	x5
x1	3	1	0	1
X2	0	0	1	0
Z’j-сj	-12	0	0	-4
Z’j-сj	0	0	0	0	0	1

Шаг 2

Запишем текущий опорный план:

X=(30000)X=(30000)

Значение целевой функции в данной точке:

Z=C⋅X=4⋅3+3⋅0+0⋅0+0⋅0+M⋅0=12

Данный опорный план не является оптимальным, так как на пересечении строки 3 и столбцов x1, x2, x3, x4 есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-4), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем min(ai,0 /ai,3), при ai,3>0, i=1,...2. min(3:1)=3 соответствует строке 1. Из базиса выходит вектор x1. Сделаем исключение Гаусса для столбца x3, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на 4

Симплекс таблица примет следующий вид:

Базис	X0	X1	x2	x3	x4	x5
x3	3	1	0	1
X2	0	0	1	0
Z’j-сj	0	4	0	0
Z’j-сj	0	0	0	0	0	1

Шаг 3

Запишем текущий опорный план:

X=(0 0 3 0 0)

Значение целевой функции в данной точке:

Z=C⋅X=4⋅0+3⋅0+0⋅3+0⋅0+M⋅0=0

Текущий опорный план является оптимальным, так как в строке 4 под переменными x1, x2, x3, x4 нет отрицательных элементов. Встроке 3 нет отрицательных элементов, а если такие есть и в данном столбце в строке 4 находится положительное число, то данный столбец не учавствует в итерации.

Решение канонической задачи без искусственных переменных можно записать так:

X∗0=(0 0 3 0 )

Решение исходной задачи:

Xmax=(0 0)

или

x1=0,x2=0x1=0,x2=0

Значение целевой функции в оптимальной точке:

Z min=Cисх⋅X∗=4⋅0+3⋅0=0

Xmax=(0 0) Zmax −48

7.1. В следующих транспортных задачах найти такие объёмы перевозок

однородной продукции от поставщиков к потребителям при которых общие з-траты на перевозку продукции будут минимальными. В таблицах заданы объёмы запасов продукции у поставщиков (Ai), объемы потребности в продукциипотребителей (Bj) и удельные затраты на перевозку единицы продукции от поставщиков к потребителям (пересечение соответствующих строк и столбцовтаблицы).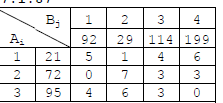

1 2