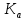Расчет константы равновесия методами статистической и классической термодинамики. Расчет константы равновесия методами статистической и классическ. "Химическая и статистическая термодинамика"
 Скачать 90 Kb. Скачать 90 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский государственный технологический институт (технический университет)» (СПбГТИ(ТУ)) Курсовая работа бакалавра 2-го курса Санкт-Петербургского государственного технологического института (технического университета) Исаджаняна Дереника Ашотовича по теме “Химическая и статистическая термодинамика” кафедра Физической химии Число___________________ Оценка__________________ Проверил_________________ (проф. Н.А.Чарыков) Санкт-Петербург 2020 Задание на курсовую работу бакалаврам 2-го курса по теме “Химическая и статистическая термодинамика” Методом статистической термодинамики (используя статистические суммы по состояниям для различных видов движения участников реакции) рассчитать константу равновесия химической реакции, протекающей в идеальной газовой фазе при температуре Т и давлении Р. Рассчитать константу равновесия этой же реакции методом классической термодинамики, используя истинные изобарные теплоемкости с помощью полиномов Темкина-Шварцмана. Сравнить полученные результаты. Вид реакции, значения Т и Р взять из Учебного пособия Ю.П.Акуловой и соавт. “Физическая химия”, СПб, СПбГТИ(ТУ), 2016, С.27 (Задание N1 “Расчет степени превращения…проведения процесса”). Номер варианта Ваш бывший + 3, номер подварианта – 2-й. Правила оформления Титульный лист. Курсовая работа бакалавра 2-го курса Санкт-Петербургского государственного технологического института (технического университета) ФИО - полностью по теме “Химическая и статистическая термодинамика” кафедра Физической химии Число___________________ Оценка__________________ Проверил_________________ (проф. Н.А.Чарыков) Санкт –Петербург -2020- Содержание Задание на курсовую работу, подписанное преподавателем на отдельном листе. Список обозначений, наименование используемых величин и констант с размерностью (на отдельном листе). Основные формулы для расчета статистических сумм и константы равновесия методом статистической термодинамики. Таблица используемый данных для расчета статистических сумм по состояниям для различных видов движения участников реакции (Молекулярные веса, давление, межатомные расстояния, валентные углы, моменты инерции, волновые числа колебаний, факторы электронного вырождения или термы молекул, стандартные теплоты образования при 0К). Приводится со ссылками на источник со страницами в источнике. Таблица рассчитанные статистических сумм разных видов движения, полных статистических сумм, стандартных теплот реакции при 0К и константы равновесия. Основные формулы для расчета константы равновесия методом классической термодинамики, используя истинные изобарные теплоемкости с помощью полиномов Темкина-Шварцмана. Таблица используемый данных для расчета констант равновесия (стандартные энтальпии, энтропии образования, коэффициенты полиномов Темкина-Шварцмана). Таблица рассчитанных изменений стандартных теплоты, энтропии, свободной энергии Гиббса, константы равновесия реакции. Сравнение константы равновесия, вычисленной 2-мя методами и объяснение расхождений, если таковые имеются. Краткие выводы по курсовой. Список литературы (отдельная страница). Правила оформления. 12 шрифт, 1.5 интервал, Times New Roman, Сквозная нумерация страниц, сквозная (по мере появления) нумерация источников – ссылок, сквозная нумерация таблиц, Наименование таблиц вверху таблицы,  Оформление ссылок по ГОСТу. СодержаниеСокращения и условные обозначения параметров, их единицы измерения 4 Основные формулы для расчета статистических сумм и константы равновесия методом статистической термодинамики 5 Основные формулы для расчета константы равновесия методом классической термодинамики 15 Выводы 18 Список литературы 19 Сокращения и условные обозначения параметров, их единицы измеренияQ – Статистическая сумма по состояниям M – Молекулярный вес [г·моль-1] T – Температура [К] P – Давление [атм] p – Парциальное давление [атм] r – Межатомное расстояние [м] ∠ – Валентный угол [град] I – Момент инерции [кг·м2] ῶe – Волновое число колебаний [м-1] θ – Характеристическая температура i-го компонента [К] gi – фактор вырождения i-го колебания g0 – Фактор вырождения основного электронного состояния σ – Коэффициент симметрии молекулы 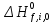 – стандартная теплота образования i-го участника реакции при 0К [кДж·моль-1] – стандартная теплота образования i-го участника реакции при 0К [кДж·моль-1]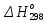 – Стандартная энтальпия образования при 298 K [кДж·моль-1] – Стандартная энтальпия образования при 298 K [кДж·моль-1]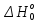 – Стандартный тепловой эффект реакции при 0 K [кДж·моль-1] – Стандартный тепловой эффект реакции при 0 K [кДж·моль-1]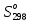 – Стандартная энтропия образования при 298 K [Дж·моль-1·K-1] – Стандартная энтропия образования при 298 K [Дж·моль-1·K-1]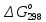 – Стандартная энергия Гиббса образования при 298 K [кДж·моль‑1] – Стандартная энергия Гиббса образования при 298 K [кДж·моль‑1]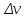 – Изменение числа молей молекул газа в реакции [моль] – Изменение числа молей молекул газа в реакции [моль]a, b, c – Коэффициенты полиномов Темкина-Шварцмана Ka – Константа равновесия реакции h = 6.62·10-34 [Дж·с] – постоянная Планка c = 3·108 [м·с-1] – скорость света в вакууме k = 1.38·10-23 [Дж·К-1] – постоянная Больцмана Энергия [Дж]/ Статистическая сумма: Eпост. /Qпост.– Энергия/статистическая сумма поступательного движения Eвращ. /Qвращ.– Энергия/статистическая сумма вращательного движения Eколеб. /Qколеб.– Энергия/статистическая сумма колебательного движения Eē /Qē– Энергия/статистическая сумма движения электронов Eяд./спин. /Qяд./спин.– Энергия/статистическая сумма ядерно-спинового движения (нуклонов) Основные формулы для расчета статистических сумм и константы равновесия методом статистической термодинамики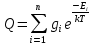 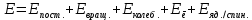 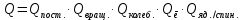 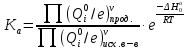 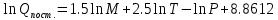 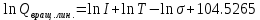 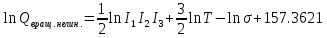 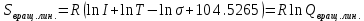 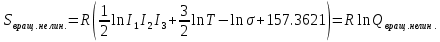 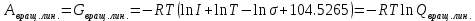 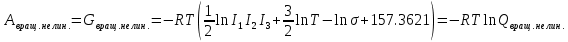 Всего независимых нормальных колебаний в молекуле (n), состоящей из N атомов: n=3N-5 для линейной молекулы, n=3N-6 – для нелинейной молекулы. 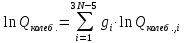 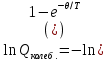 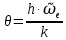 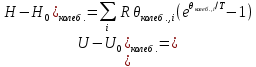 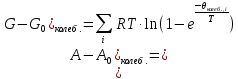 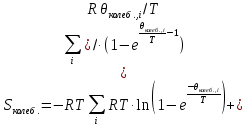 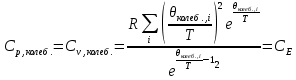 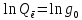 приT <2000 К приT <2000 К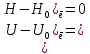 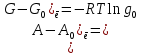 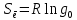 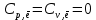 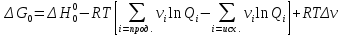 Таблица 1. Данные для расчета статистических сумм по состояниям для различных видов движения участников реакции [1, С. 178]
Поступательное движение Расчет значений поступательной составляющей суммы по состояниям для данных веществ при Р = 1 атм. и Т = 700 К.  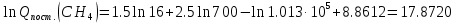 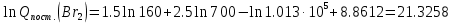 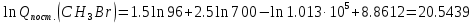 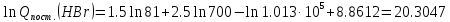 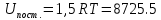 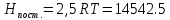 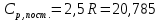 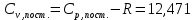 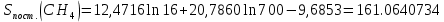 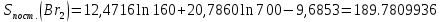 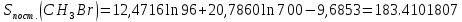 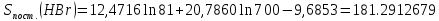 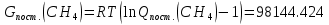 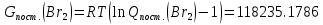 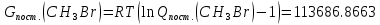 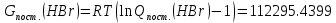 Вращательное движение Расчет значений вращательной составляющей суммы по состояниям для данных веществ. 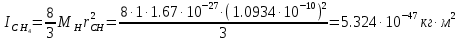 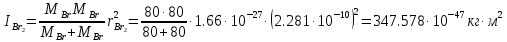 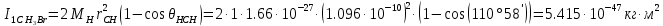 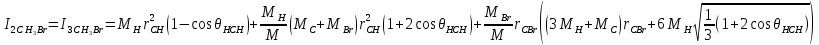 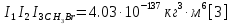 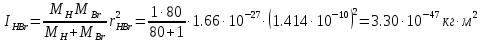 Коэффициенты симметрии 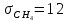 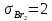 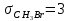 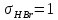 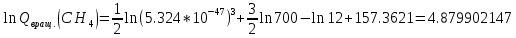 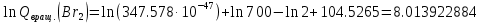 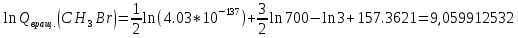 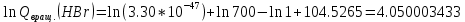 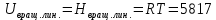 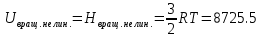 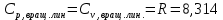 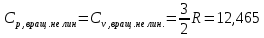 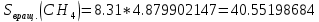 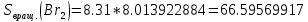 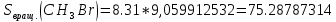 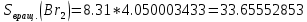 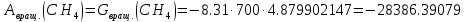 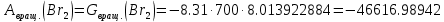 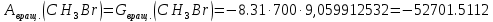 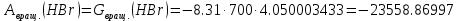 Колебательное движение Расчет независимых характеристических колебаний: 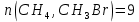 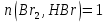 Расчет значений вращательной составляющей суммы по состояниям для данных веществ 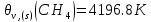 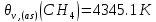 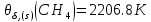 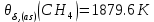 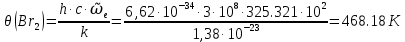 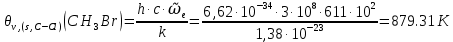 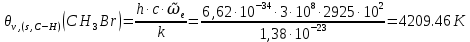 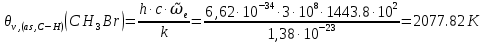 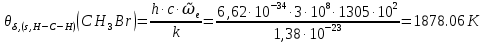 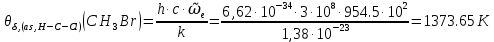 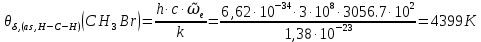 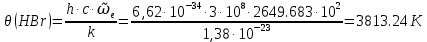 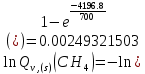 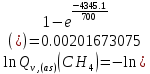 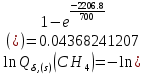 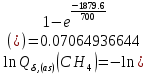 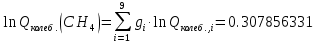  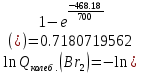 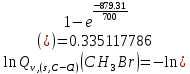 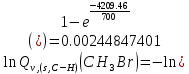 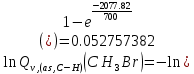 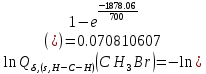 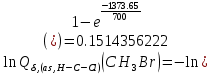 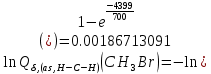 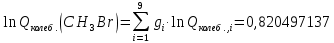 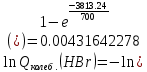 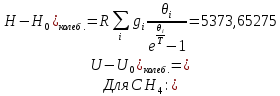 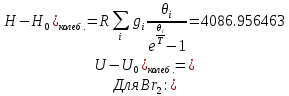 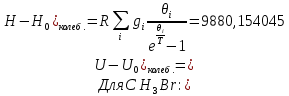 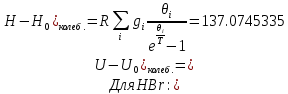 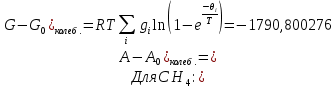 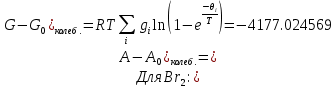 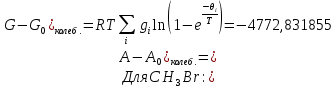 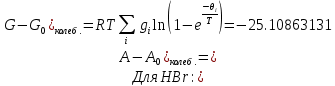 Колебательная энтропия Эйнштейна: 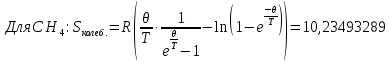 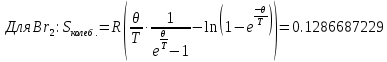 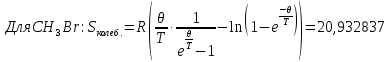 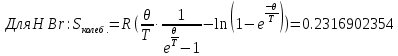 Колебательная теплоемкость Эйнштейна: 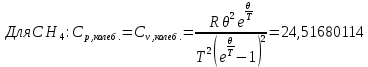 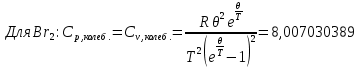 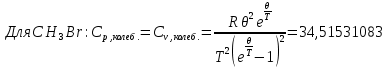 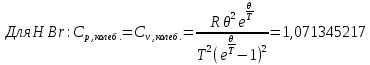 Движение электронов Расчет значений составляющей движения электронов суммы по состояниям для данных веществ. Так как T <2000 К 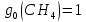 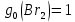 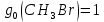 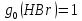 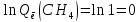 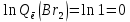 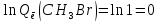 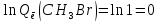 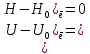 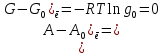 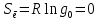 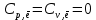 Расчет константы равновесия через статистические суммы по состоянию молекул идеального газа. 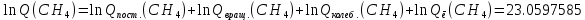 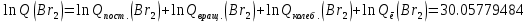 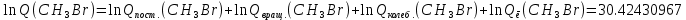 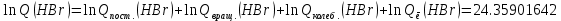 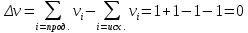 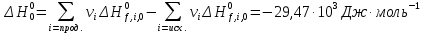 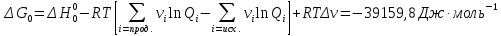 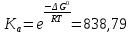 Таблица 2. Рассчитанные статистические суммы разных видов движения, полные статистические сумм, стандартные теплоты реакции при 0К и константа равновесия.
Основные формулы для расчета константы равновесия методом классической термодинамики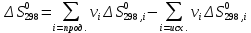 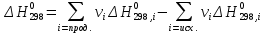 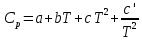 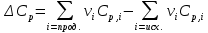 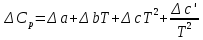 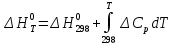 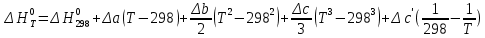 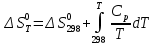 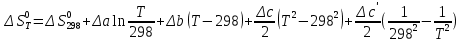 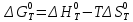 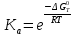 Реакция: 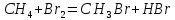 Таблица 3. Данные для расчета констант равновесия методом классической термодинамики [1, С. 72-89]
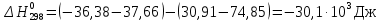 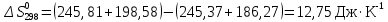 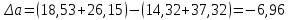 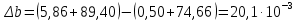 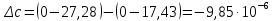 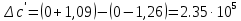 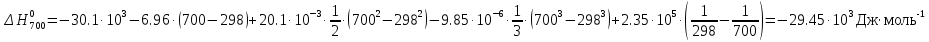 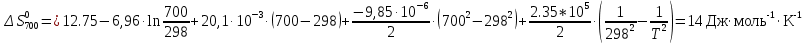 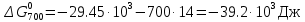 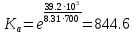 Таблица 2. Рассчитанные изменения стандартных теплоты, энтропии, свободной энергии Гиббса, константа равновесия реакции.
ВыводыВ рамках данной курсовой работы при помощи методов статистической и классической (используя истинные изобарные теплоемкости с помощью полиномов Темкина-Шварцмана) термодинамики была рассчитана константа равновесия гомогенной реакции CH4(г) + Br2(г)= CH3Br(г) + НBr(г) при температуре T = 600 К и давлении P = 1 атм. Константа равновесия, полученная при помощи методов классической термодинамики, оказалась равна 844,6. Константа равновесия, полученная при помощи методов статистической термодинамики, оказалась равна 838,79 Результаты хорошо коррелируют между собой, что подтверждает одинаковую работоспособность двух различных методов. Список литературыКраткий справочник физико-химических величин / Н.М. Барон и [и др.]; под ред. А.А. Равделя и А.М. Пономаревой. – 11-е изд. испр. и доп. – М.: ООО «ТИД «Аз-book», 2009. – 240 с. Физическая химия [Текст]: учебное пособие / Ю. П. Акулова, С. Г. Изотова, О. В. Проскурина, И. А. Черепкова. – СПб.: СПбГТИ (ТУ). – 2016. – 192 c. Рассчитано с помощью программы Gaussian 09 Термические константы веществ. Справочник в 10 выпусках/Отв. ред. Глушко В. П. М.: Изд-во ВИНИТИ АН СССР, 1965-1982 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

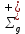
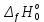 , Дж·моль-1
, Дж·моль-1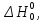 Дж·моль-1
Дж·моль-1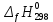
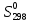
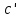 ·10-5
·10-5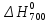 , Дж
, Дж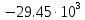
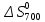 , Дж·K-1
, Дж·K-1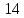
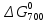 , Дж
, Дж