ФТТ. Краткие определения. Симметрия и свойства кристаллов
 Скачать 61.43 Kb. Скачать 61.43 Kb.
|
|
Симметрия и свойства кристаллов. Конденсированное состояние вещества – совокупность сильновзаимодействующих части (межатомные расстояния такие, что сохраняется баланс сил притяжения и отталкивания) Кристаллы всегда растут в форме правильных, симметричных многогранников. Симметрия - свойство кристаллов идеальных по форме, структуре и физическим свойствам повторять в себе свои части и особенности. Симметрия – свойство объекта совмещаться с самим собой при определенных перемещениях, в нашем случае при перемещениях в пространстве. Спайность - особенность кристаллов с большей или меньшей легкостью раскалываться по некоторым определённым направлениям (плоскостям). Свойства кристаллов: Атомарное строение Однородность свойств Трансляционно-упорядоченное строение Инвариантность Анизотропия – зависимость равновесных физических свойств от направления. Полный набор операции симметрии, присущих данному объекту, составляет его группу симметрии. Анизотропия и симметрия физических свойств кристаллов является характерной особенностью кристаллов и обуславливается закономерностью и симметрией их внутреннего строения. Идеальный кристалл Идеальный кристалл – однородная, анизотропная симметричная конденсированная среда, обладающая трансляционно-упорядоченным атомным строением и способную самоограняться в процессе роста. В идеальном кристалле нет дефектов, тепловых колебаний и частицы в нем расположены идеальными параллельными рядами (порядок А) Примитивной элементарной ячейкой называем ячейку, в которой нет узлов. Условия примитивных ячеек: Наилучшим образом отражают симметрию По возможности имеют прямые углы Обладают минимальной площадью Площадь каждой элементарной ячейки постоянная и одинаковая. Регулярная плотность сетки – число узлов на единицу площади. Пространственная решетка Пространственная решетка – трехмерная система эквивалентных узлов. Трансляционная группа – основная тройка трансляций (выбирается аналогично плоской сетке) Элементарная ячейка – параллелепипед, построенный на трехмерных элементарных трансляциях. Характеристиками являются длины отрезков a, b, c и углами α, β, γ. Кристаллическая решетка – совокупность всех трансляций кристаллического пространства. Ячейка Вигнера-Зейтца Самая симметричная из примитивных. Она полностью определяет трансляционную структуру кристалла и имеет точечную симметрию. Символы рядов Символ ряда характеризует семейство параллельных рядов и ребер многогранника. Направление определяется двумя точками: началом координат и любым узлом ряда. Символ второго узла принимают за символ ряда. Общее направление называют осью зоны ( они не зависят от углов между осями и осевых отрезков) Индексы Миллера характеризуют наклон плоскости к осям координат (направляющие косинусы) Замечание: чем проще символ плоскости, т.е. чем меньше значение индексов, тем больше ретикулярная плотность этой плоскости (т.е. число узлов) и тем больше межплоскостные расстояния. Они чаще всего встречаются – закон Бравэ. Элементы симметрии Симметричной фигурой называется такая, которая может совместится сама с собой в результате симметричных преобразований. Отражение и вращения, приводящие многогранник в совмещение с самим собой, называются преобразованиями симметрии или симметричными операциями. Воображаемые плоскости, линии и точки, с помощью которых определяются эти отражения и вращения, называются элементами симметрии. 1 рода – плоскости симметрии, оси симметрии, центр симметрии. Симметричное преобразование в центре симметрии – это зеркальное отражение в точке. Ось симметрии – прямая линия при повороте вокруг которой на некоторый определённый угол фигура совмещается сама с собой. 2 рода – инверсионная ось симметрии. Зеркально-поворотная ось представляет собой совместное действие поворота вокруг оси симметрии и отражения в плоскости симметрии, перпендикулярной этой оси. Сингония – подразделение кристаллов по конфигурации их элементарной ячейки. Кристаллические сингонии – это подразделение кристаллов по симметрии формы их элементарной ячейки или, что то же самое, по точечной симметрии узлов кристаллической решетки. Сингонии характеризуется соотношениями между длинами рёбер элементарные ячейки и углами между ними. Виды сингоний: Триклинная Моноклинная Ромбическая Тригональная Тетрагональная Гексагональная Кубическая Нужно учесть центрированность – решетки Бравэ. Виды решеток Бравэ: Примитивные Объемноцентрированные Гранецентрированные Базоцентрированные Решётки Браве образуются действием только операций трансляций на любую точку кристалла и из неё выводят систему узлов. Обратная решетка Строится на векторах, найденных через векторное произведение: 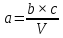 Зона Бриллюэна Имеет границы 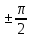 Протяженность 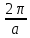 Тензоры Вызванные обобщенными силами обобщенные потоки в первом, линейном приближении пропорциональны внешним силам. При этом свойства среды описываются тензорами. Физическое свойство – характеристика вещества или способность тела реагировать на внешнее воздействие (часто описывается тензорами) Скаляры – одно число Векторы – определены только по отношению к направлению Тензор – момент инерции Главные оси Важным свойством поверхностей второго порядка является то, что они обладают главными осями – тремя лежащими под прямыми углами друг к другу направлениями, по отношению к которым, взятых за оси координат, общее уравнение приводится к виду 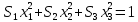 Симметричный тензор второго ранга, также как и любая поверхность второго порядка, при приведении к главным осям принимает простейшую форму: 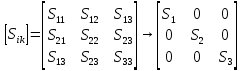 Числа на главной диагонали – главные компоненты тензора. Основное свойство тензора – это закон преобразования его компонент при вращении системы координат. Компоненты тензора второго ранга при вращении системы координат преобразуются подобно парным произведениям координат точки. Определение главных значений и осей тензора второго ранга подобно задачам, которые решаются в квантовой механике. Инварианты – это величины, сохраняющие неизменное значение при переходе к новым координатам. Феноменологические коэффициенты образуют тензор второго ранга, поскольку они связывают вектора сил и потоков. Соотношение Онзагера: 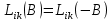 Различия между материальными и полевыми тензорами связаны с их разной природой. Так тензоры описывающие различные физические свойства кристаллов имеют определённую ориентацию в кристалле и имеют симметрию точечной группы кристалла. Они называются материальными тензорами. Примером полевого тензора является тензор напряжений. Тензоры напряжений и тензоры деформаций могут иметь любую ориентацию в кристалле и имеют смысл как для изотропных тел (стекла), так и анизотропных кристаллов. Они не описывают каких-либо свойств кристалла, они близки по смыслу к термину «сила», приложенной к кристаллу, и подобно электрическому полю могут иметь произвольное направление в кристалле. Такие тензоры называются полевыми. Диа и парамагнетики Магнитная восприимчивость диамагнитных и парамагнитных кристаллов является типичным анизотропным свойством, описываемым тензором второго ранга. Диа и парамагнитные эффекты почти не зависят от формы кристалла. Электрическая поляризация Описывается тензором второго ранга. Аналогично намагниченности. Диэлектрические свойства кристалла могут быть охарактеризованы значениями и направлениями трёх главных диэлектрических проницаемостей или диэлектрических восприимчивостей, которые в общем случае зависят от частоты электрического поля. Различия между намагниченностью и поляризацией: Нет магнитных зарядов – магнитные поля создаются за счет движения электрических зарядов, а магнитные моменты – орбитальным и спиновым моментами электронов. Эффект деполяризации – при поляризации в электрическом поле возникает деполяризующее поля (противодействующее) Утечка заряда - в реальных диэлектриках существуют микротрещины, дислокации, области скопления примесей, на которых могут быть заряды, эти заряды мигрируют и со временем уменьшают электрическое поле поляризационных зарядов. Пироэлектричество Пироэлектрический эффект – приобретают или изменяют поляризацию при изменении температуры (он не сохраняется). Пироэлектрический эффект является первым физическим свойством кристалла, которой описывается коэффициентом, являющимся вектором. По принципу Неймана этот эффект должен иметь симметрию не ниже точечной группы кристалла. Он не может существовать в кристаллах с центром инверсии. Вектор p должен быть параллелен особенному направлению в кристалле, неповторяемому никакими элементами точечной группы Полярный вектор – направление, два конца которого не могут быть совмещены никаким элементом симметрии точечный группы (Не все они особенные) Динамика кристаллической решетки Подсистемы в кристаллах: электронная и решеточная. В кристаллической решетке атомы всегда колеблются около узлов (даже при 0К – нулевые колебания). Смещение из равновесия аналогично сдвигу из потенциальной ямы, но нельзя считать частицы осцилляторами, потому что важно учитывать частицы вокруг. Если рассмотреть цепочку одноатомных атомов, то для нее получится, что закон дисперсии будет иметь вид: 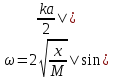 Закон дисперсии – периодическая функция волнового вектора. Все физически неэквивалентные колебательные состоянии кристалла, которые характеризуются волновым вектором к, лежат в пределах 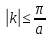 (Зона Бриллюэна) (Зона Бриллюэна)А все другие колебательные состояния кристаллической решетки физически эквивалентны этим. Если рассмотреть область малых к (больших длин волн), то можно получить, что колебания аналогичны звуковым. Если рассмотреть двухатомную цепочку, то мы получим аналогичное решение, но в два раза меньший линейный период. Каждому значению к соответствуют два решения – две ветви колебаний: оптическая и акустическая. 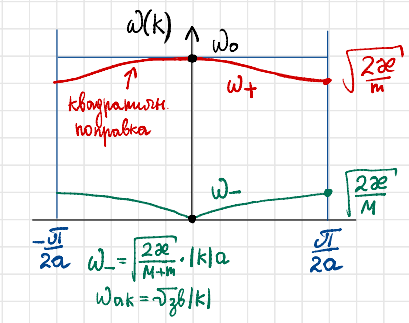 Почему эти колебания называются оптическими? Пусть кристалл обладает некой долей ионности. Тогда атомам присущ некий эффективный положительный и отрицательный заряд. Эти атомы колеблются в противофазе, то есть движутся навстречу друг другу. Возникает переменный электрический диполь. Колеблющийся диполь может либо поглощать, либо изучать электромагнитные волны. Оказывается, что это излучение попадает в оптический диапазон (реально в дальний ИК диапазон). Интересно, атомы разные, массы разные, а колеблются они с одинаковой амплитудой, то есть элементарная ячейка колеблется как единое целое. Это свойство звуковых колебаний. Близкорасположенные точки среды колеблются с одной и той же амплитудой. И нижняя ветвь называются акустической. Теорема: Подходящим выбором системы координат движение любой системы частиц, совершающих малые колебания, может быть сведено к движению независимых осцилляторов. Для этого введём так называемые нормальные координаты. Полная энергия колебаний атомов всей цепочки равна сумме кинетической и потенциальной энергии всех осцилляторов + потенциальная энергия в состоянии равновесия. Полная тепловая энергия колебаний атомов в цепочке складывается из энергии нормальных колебаний, ведущих себя подобно линейным гармоническим осцилляторам с собственной частотой Количество таких осцилляторов равно количеству степеней свободы у всех атомов, если в одномерной цепочке N атомов, то и осцилляторов будет N штук. Квантово-механические обобщения Энергия гармонических колебаний осциллятора квантована. Даже при 0 К атомы не могут находиться в положениях равновесия, то есть совершают колебания. Точная локализация атомов невозможно в силу соотношения неопределённости Гейзенберга. Фонон – квазичастица, которая сопоставляется каждому нормальному коллективному колебанию с фиксированной частотой и длиной волны. Мы не можем говорить о независимых колебаниях каких-либо атомов. Движение всех атомов взаимозависимо. Но мы можем говорить о распространении по кристаллу волн смещений атомов с фиксированной частотой – эти волны есть фононы. Поэтому возбуждение какого-либо нормального колебания есть на языке квазичастиц рождение фонона с такой-то частотой и волновым вектором. Фонон несёт наименьшую энергию, его рассматривают как элементарное возбуждение. «Сложное» возбуждение есть просто возбуждение, содержащие много фононов. Таким образом, коллективные движения атомов в кристалле представляют собой звуковые волны, а соответствующие им возбуждения – кванты звука или фононы. Фонон – это квант колебательной энергии кристалла. Статистика фононов Являются бозонами, так как для них принцип Паули не существует. 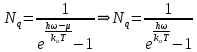 В трехмерном пространстве все аналогично. Акустические колебания – элементарная ячейка колеблется в целом – три степени свободы, три типа акустических колебаний, фононов. Оптические колебания – элементарная ячейка покоится, атомы колеблются навстречу друг другу. В трёхмерном кристалле 3s типов колебаний. Из них три акустические ветви, а остальные (3s-3) – оптический ветви. Температура Эйнштейна – температура, при которой начинается быстрый спад теплоемкости. Температура Дебая – температура максимальных акустических колебаний. Циклические условия Условие цикличности 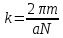 Элементы зонной теории Если потенциал периодичен, то волновые функции и допустимые энергии обладают целым рядом уникальных свойств. Потенциал периодичен, а они вовсе не обязательно должны быть периодичными. А что должно быть периодичным так это электронная плотность. Однородное дифференциальное уравнение при заданных граничных условиях имеет единственное решение. Такое возможно только если эти две волновые функции отличаются максимум на константу Теорема Блоха: 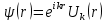 Где 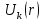 – блоховская амплитуда, которая имеет тот же период, что и потенциал (2а) – блоховская амплитуда, которая имеет тот же период, что и потенциал (2а) |
