Методичка_ФФ-106. Методические указания Челябинск 2015 Тема I. Индексные обозначения тензоров
 Скачать 2.72 Mb. Скачать 2.72 Mb.
|
|
Министерство образования и науки Российской Федерации Челябинский государственный университет Математический факультет Кафедра вычислительной механики и информационных технологий ВЕКТОРНЫЙ И ТЕНЗОРНЫЙ АНАЛИЗ Методические указания Тема I. Индексные обозначения тензоров. Развитие науки привело к необходимости введения более сложного понятия, чем скалярная величина или вектор. Новый математический объект тензор объединяет такие понятия как скаляр и вектор. Скалярная величина – это тензор нулевого ранга, вектор – это тензор первого ранга. Индексная запись тензора – это компактная и наиболее удобная форма его записи. Сформулируем правило суммирования для индексной формы записи тензора. Один и тот же индекс у тензора может встретиться один раз или дважды. Неповторяющийся индекс называется свободным, число свободных индексов определяет ранг тензора. Индекс, встречающийся дважды (повторяющийся индекс), является индексом суммирования, знак суммы не пишется, а подразумевается. Каждый буквенный индекс тензора может принимать значения 1, 2, … , N, где N – размерность индекса. Не теряя общности, будем в дальнейшем считать, что N=3. Примеры записи тензоров в индексной форме: 1) 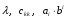 – тензоры нулевого ранга не имеют свободных индексов и определяются одним числом; – тензоры нулевого ранга не имеют свободных индексов и определяются одним числом;2) 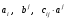 – тензоры первого ранга имеют один свободный индекс, и определяются упорядоченным набором из трех чисел (размерность индекса равна трем); – тензоры первого ранга имеют один свободный индекс, и определяются упорядоченным набором из трех чисел (размерность индекса равна трем);3) 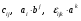 – тензоры второго ранга имеет два свободных индекса, и определяются девятью числами; – тензоры второго ранга имеет два свободных индекса, и определяются девятью числами;4) 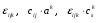 – тензоры третьего ранга, имеет три свободных индекса, и определяется 27-ю числами; – тензоры третьего ранга, имеет три свободных индекса, и определяется 27-ю числами;5) и т.д. Задача 1. В трехмерном евклидовом пространстве раскройте индексное выражение: 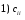 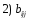 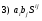 Решение. 1) Это тензор нулевого ранга, т.е. скалярная величина, ее определяет одно число: 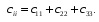 2) Это тензор первого ранга. Один свободный индекс i определяет ранг этого тензора. Повторяющийся индекс j является индексом суммирования. Распишем тензор первого ранга как вектор: 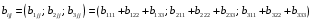 3) Это тензор нулевого ранга, т.е. скалярная величина. Повторяющиеся индексы i и j являются индексами суммирования. Раскроем последовательно сумму сначала по индексу i, а затем по индексу j: 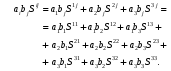 Задача 2. В трехмерном евклидовом пространстве раскройте индексное выражение: 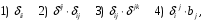 где 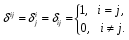 – символ Кронекера. – символ Кронекера.Решение. 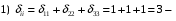 это тензор нулевого ранга. это тензор нулевого ранга.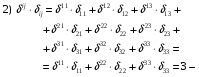 это тензор нулевого ранга. это тензор нулевого ранга.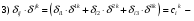 это тензор второго ранга, состоит из 9-ти компонент. это тензор второго ранга, состоит из 9-ти компонент.Раскрывая индексное выражение, получим 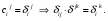 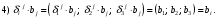 Это тензор первого ранга, окончательно запишем результат, которым будем пользоваться в дальнейшем 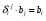 Задача 3. В трехмерном евклидовом пространстве раскройте индексное выражение: 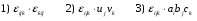  То есть имеем 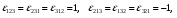 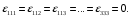 Решение. 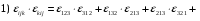 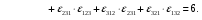 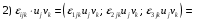 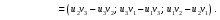 Можно показать, что это индексная запись векторного произведения векторов в декартовой системе координат, где 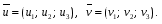 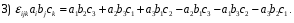 Эта индексная запись соответствует смешанному произведению векторов: 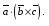 Тема II. Локальный базис криволинейной системы координат. Пусть М х1х2х3 – некоторая криволинейная система координат, а 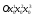 – вспомогательная декартова прямоугольная система координат. Известны функции – вспомогательная декартова прямоугольная система координат. Известны функции 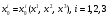 , которые связывают, декартовы и криволинейные координаты, тогда локальный базис криволинейной системы координат определим как частные производные радиус-вектора точки по криволинейной координате. Мы получим тройку векторов, зависящих от выбора точки, в которой строится базис. Векторы локального базиса меняют направление и величину при переходе от одной точки к другой. , которые связывают, декартовы и криволинейные координаты, тогда локальный базис криволинейной системы координат определим как частные производные радиус-вектора точки по криволинейной координате. Мы получим тройку векторов, зависящих от выбора точки, в которой строится базис. Векторы локального базиса меняют направление и величину при переходе от одной точки к другой.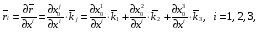 где 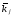 – ортонормированный базис декартовой системы координат, т.е. – ортонормированный базис декартовой системы координат, т.е.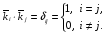 Рассмотрим различные криволинейные системы координат. I. Полярная система координат 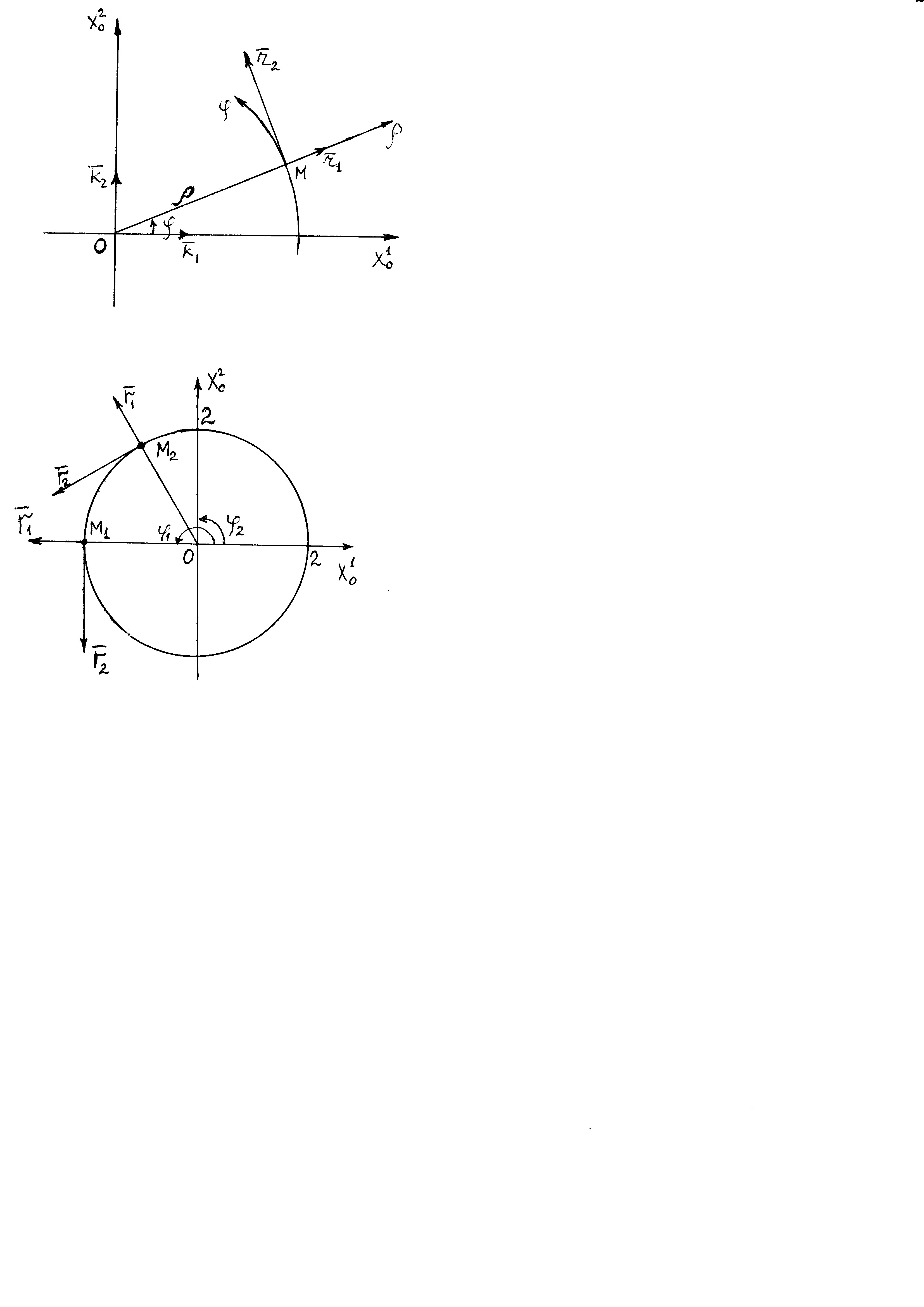 1) Введем полярные координаты: 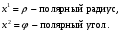 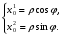 2) Определим векторы локального базиса в точке 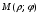 : :Рис. 1 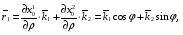 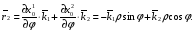 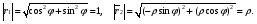 3) Построим локальный базис в точке М (рис. 1), для этого проведем через эту точку координатные линии полярной системы координат. Вдоль координатной линии изменяется только одна координата. Поэтому фиксируем каждую из координат и проводим координатную линию другой координаты. В точке М строим векторы локального базиса, которые являются касательными векторами, направленными в сторону возрастания соответствующей координаты. Длины векторов локального базиса, определяются их модулями. Построим локальные базисы в точках М1(2; 2π/3), М2(2; π), рис. 2. 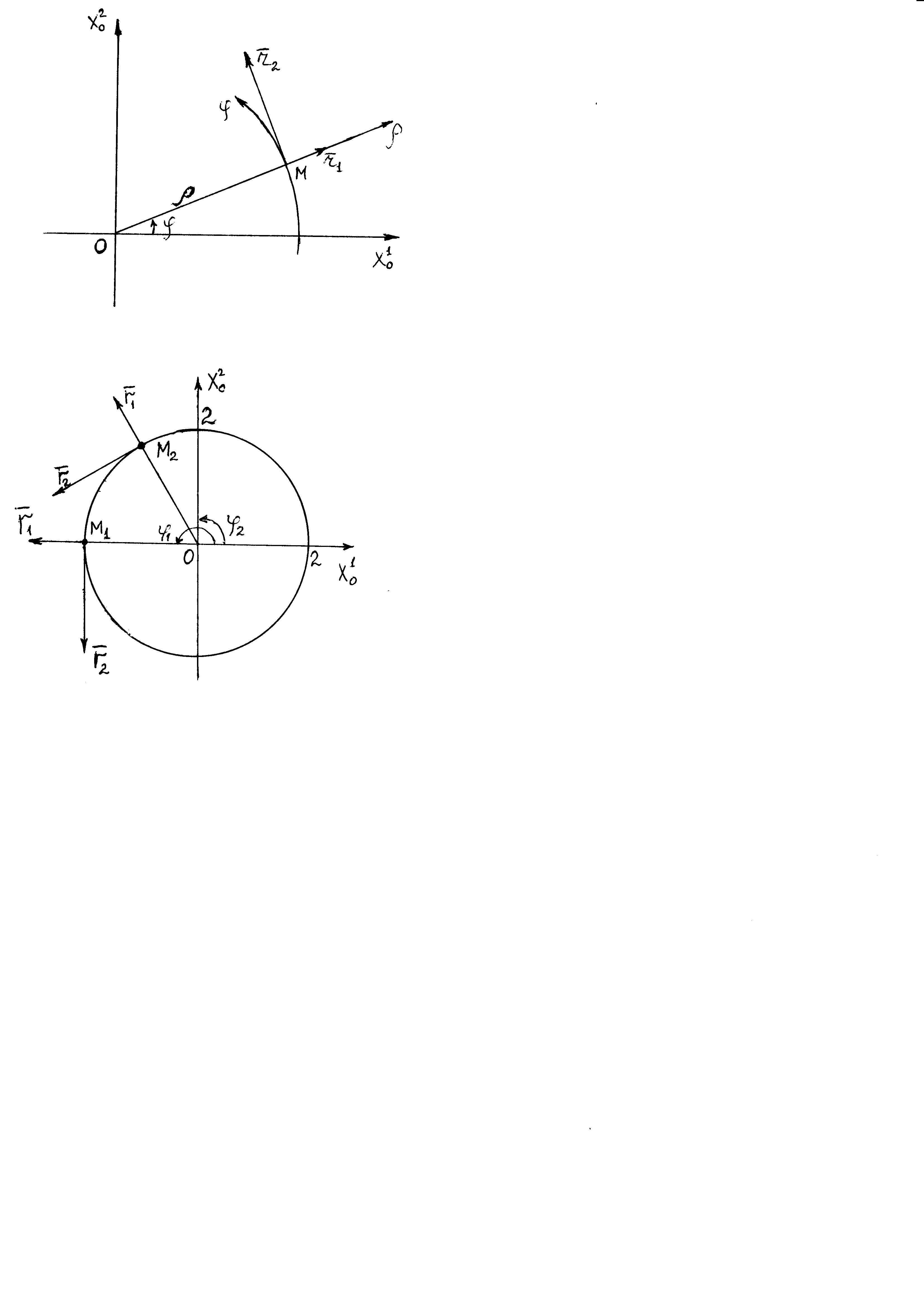 Рис. 2 II. Цилиндрическая система координат 1) Введем цилиндрические координаты: 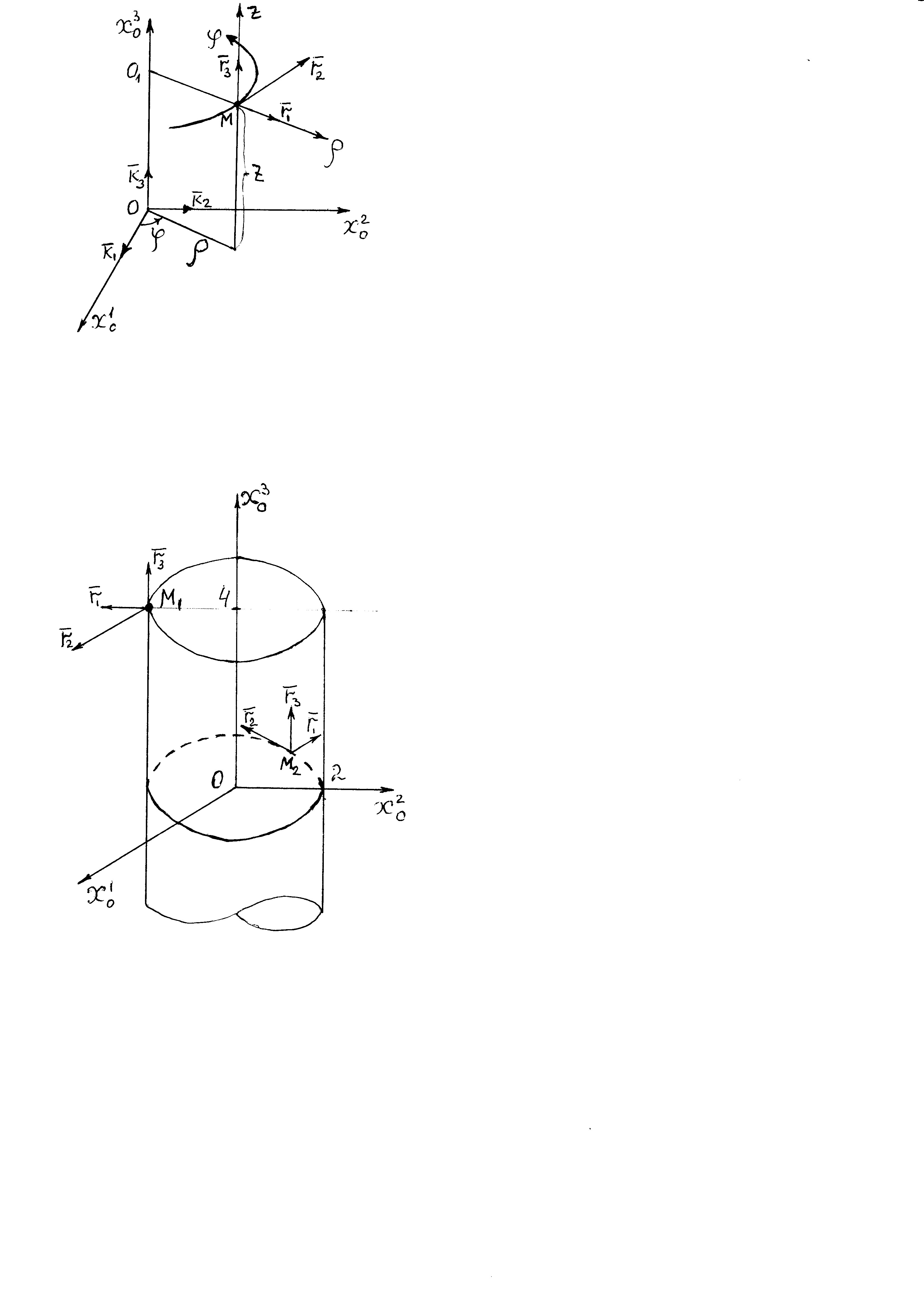 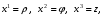 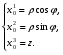 2) Определим векторы локального базиса в точке 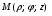 : :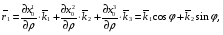 Рис. 3. 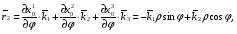 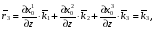 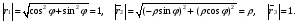 3) Построим локальный базис в точке М (Рис. 3), для этого проведем через эту точку координатные линии цилиндрической системы координат. Вдоль координатной линии изменяется только одна координата. Поэтому фиксируем две координаты и проводим координатную линию третьей координаты. В точке М строим векторы локального базиса, которые являются касательными векторами к координатным линиям. Базисные векторы направлены в сторону возрастания соответствующей координаты. Длины векторов локального базиса, определяются их модулями. Построим локальные базисы в точках М1(2; 3π/2; 4), М2(2; π; 0), рис. 4. 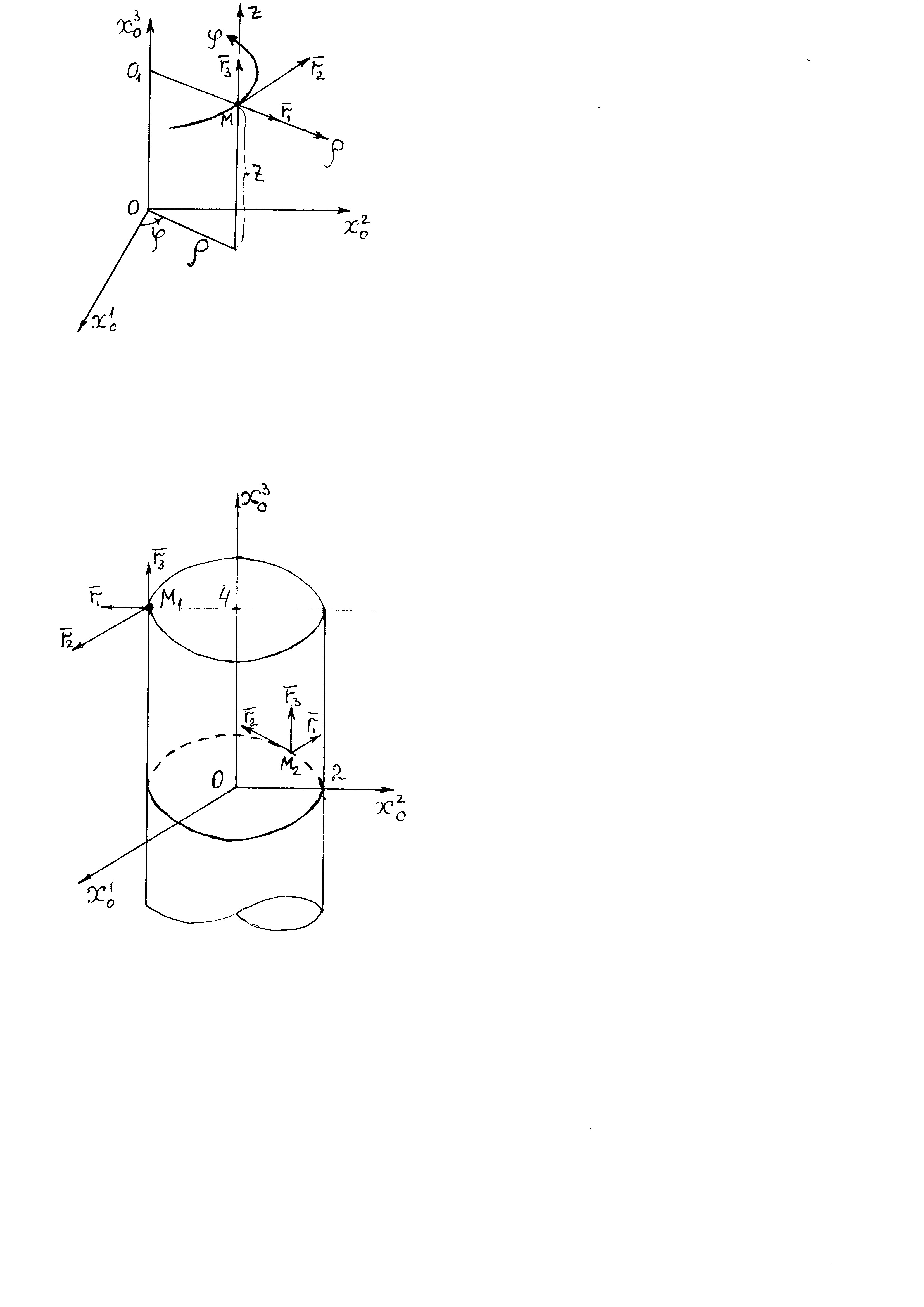 Рис. 4 III. Сферическая система координат 1) Введем сферические координаты: 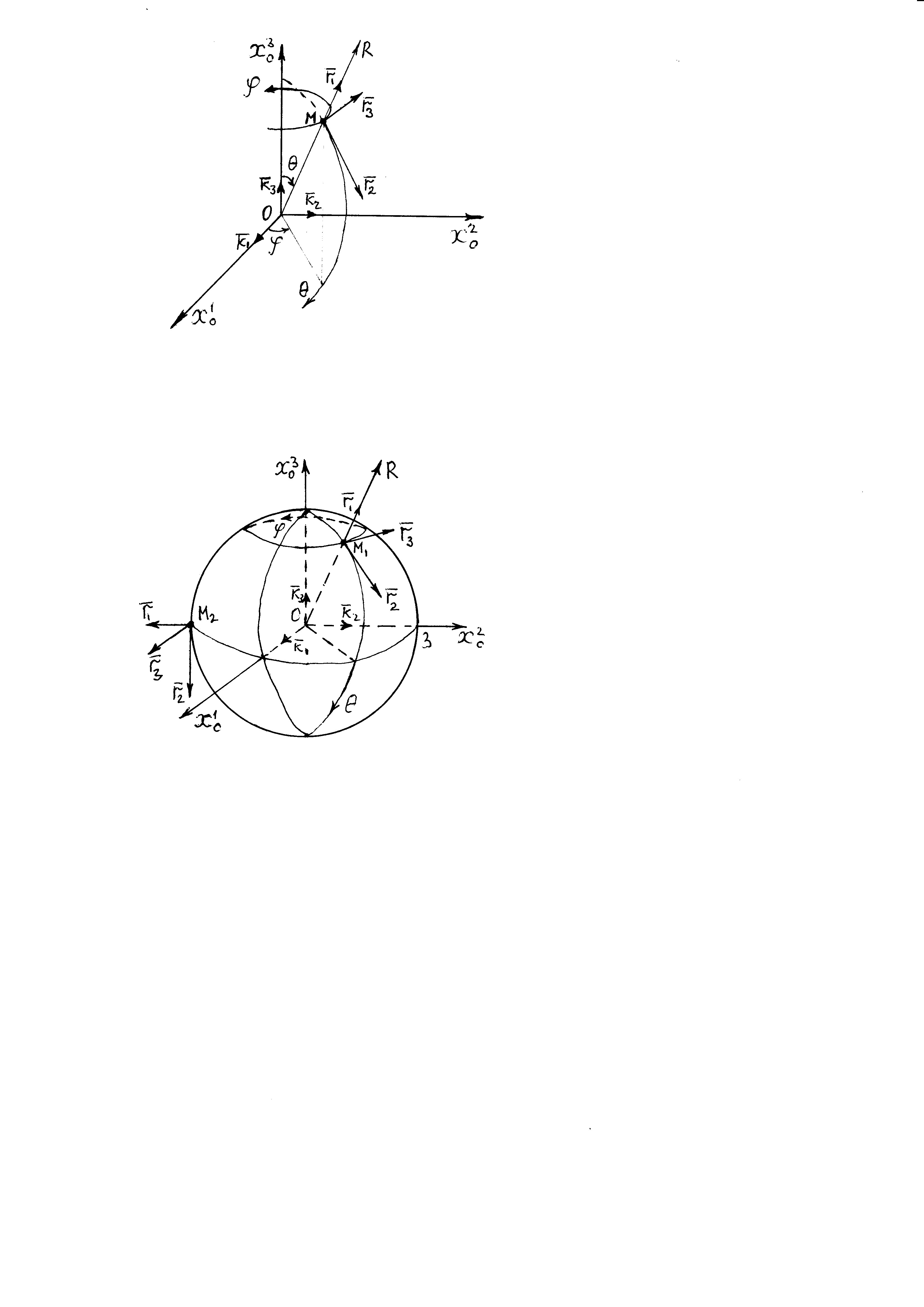 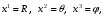 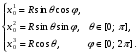 Рис. 5 2) Определим векторы локального базиса в точке 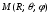 : :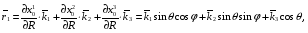 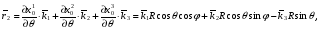 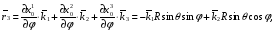 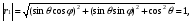 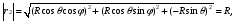 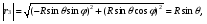 т.к. 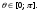 3) Построим локальный базис в точке М, для этого проведем через эту точку координатные линии сферической системы координат. Вдоль координатной линии изменяется только одна координата. Поэтому фиксируем две координаты и проводим координатную линию третьей координаты. В точке М строим векторы локального базиса, которые являются касательными векторами к координатным линиям. Базисные векторы направлены в сторону возрастания соответствующей координаты. Длины векторов локального базиса, определяются их модулями. Построим локальные базисы в точках М1(3; π/6; π/4), М2(3; π/2; 3π/2). Рис. 6. 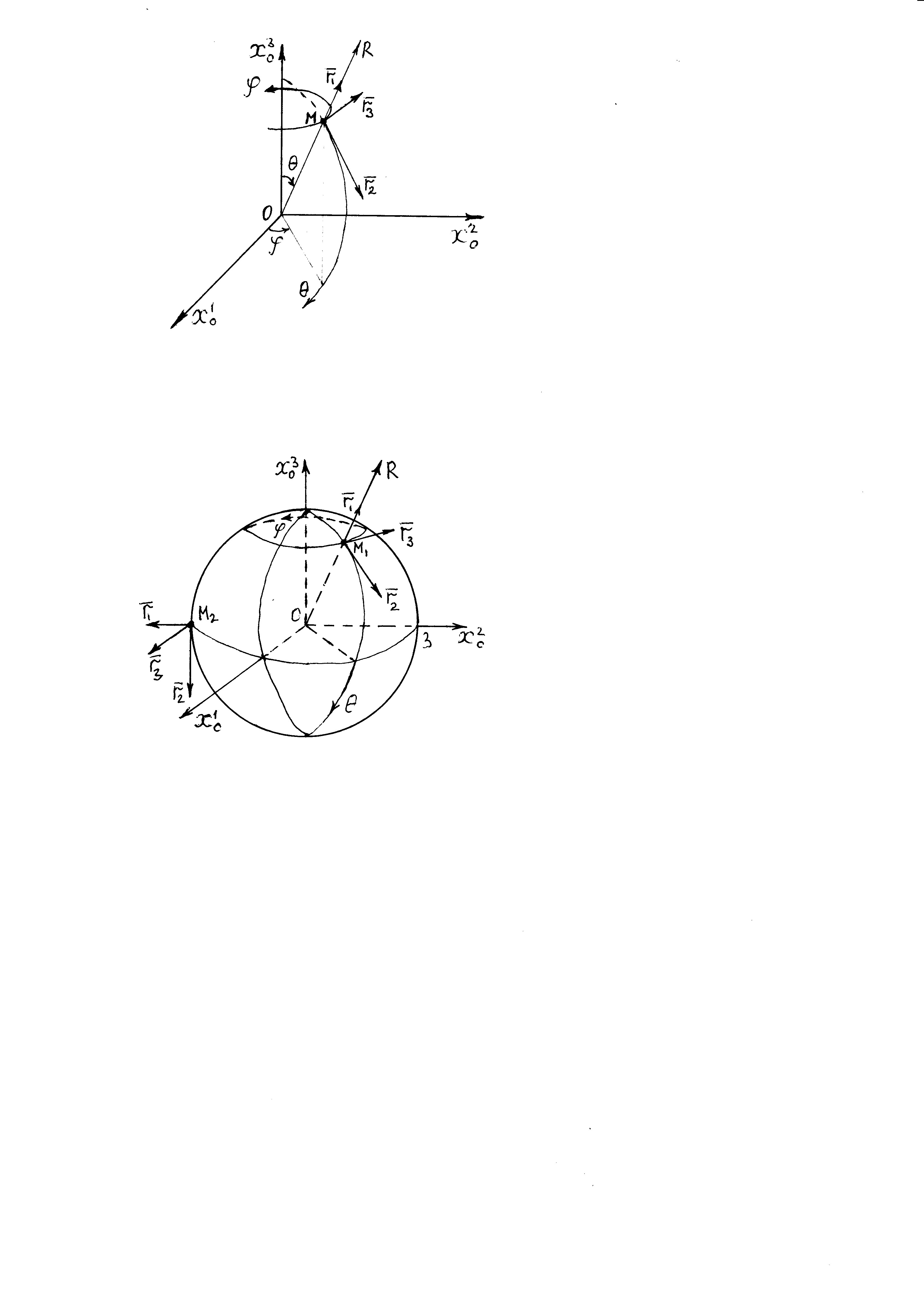 Рис. 7 IV. Тороидальная система координат. Эту систему координат изучите самостоятельно. Тема III: Взаимный базис, ковариантные и контравариантные компоненты вектора. Основные формулы: 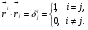 – определение взаимного базиса ri – определение взаимного базиса ri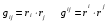 – фундаментальная матрица. – фундаментальная матрица.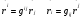 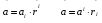  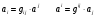 I. Цилиндрическая система координат Определим элементы фундаментальной матрицы, для этого составим скалярные произведения векторов локального базиса. 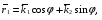 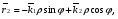 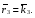 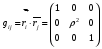 и и 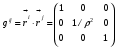 Матрица gij определена как обратная к матрице gij. Это было доказано в лекции. Матрица диагонального вида, следовательно, цилиндрическая система координат это ортогональная криволинейная система координат. Найдем векторы взаимного базиса для этой системы координат. 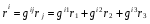 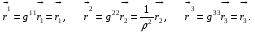 II. Сферическая система координат Определим элементы фундаментальной матрицы, для этого составим скалярные произведения векторов локального базиса. 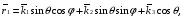 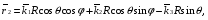 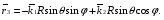 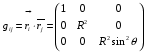 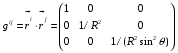 Матрица gij определена как обратная к матрице gij. Фундаментальная матрица диагонального вида, следовательно, сферическая система координат это ортогональная криволинейная система координат. Найдем векторы взаимного базиса для этой системы координат. 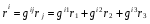 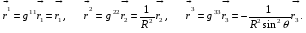 Задача 1. Известны контравариантные компоненты вектора 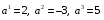 в точке в точке 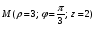 цилиндрической системы координат. Найдите ковариантные компоненты этого вектора в точке М. цилиндрической системы координат. Найдите ковариантные компоненты этого вектора в точке М.Решение. Для нахождения ковариантных компонент вектора воспользуемся формулой 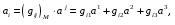 тогда получим 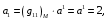 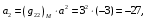 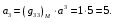 Ответ: 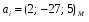 Задача 2. Известны координаты вектора а в декартовой прямоугольной системе координат 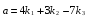 . Найдите ковариантные и контравариантные компоненты этого вектора в точке . Найдите ковариантные и контравариантные компоненты этого вектора в точке 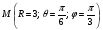 сферической системы координат. сферической системы координат.Решение. Определим векторы локального базиса в точке М сферической системы координат 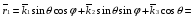 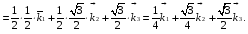 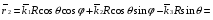 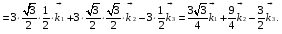 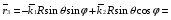 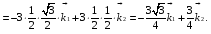 Найдем ковариантные компоненты вектора в точке М, как скалярные произведения данного вектора на базисные векторы. 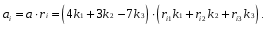 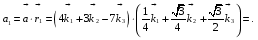 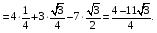 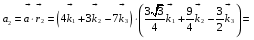 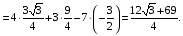 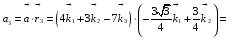 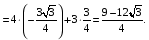 Найдем контравариантные компоненты вектора в точке М с помощью фундаментальной матрицы и найденных ковариантных компонент вектора. 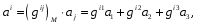 где 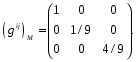 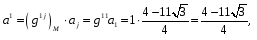 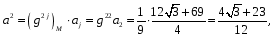 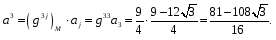 Ответ: 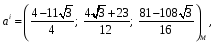 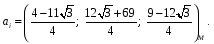 Тема IV. Определение тензора Определение. Экстенсив Q называется m-раз ковариантным и n-раз контравариантным тензором ранга m+n, если его компоненты преобразуются по закону 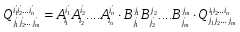 где 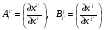 – матрицы Якоби преобразования криволинейных координат. – матрицы Якоби преобразования криволинейных координат.Задача 1. Задан смешанный тензор второго ранга 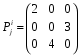 и матрица прямого преобразования криволинейных координат 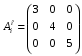 . Найдите тензор в новых осях. . Найдите тензор в новых осях.Решение. Запишем определение смешанного тензора второго ранга, т.е. закон преобразования его компонент при переходе к новой системе координат 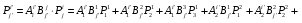 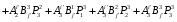 Подставим компоненты тензора в «старых» осях из условия задачи, тогда получим 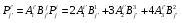 Найдем матрицу обратного преобразования координат, как матрицу обратную к матрице прямого преобразования координат 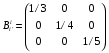 Определим компоненты тензора в «новых» осях 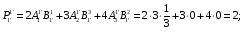 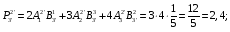 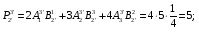 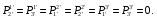 Ответ: 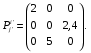 Замечание. Для дважды ковариантного тензора второго ранга и дважды контравариантного тензора второго ранга используются следующие законы преобразования 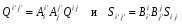 Задача 2. Задан декартов тензор второго ранга 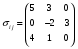 Найдите тензор в новых осях, полученных путем поворота старых на угол 450 относительно оси Найдите тензор в новых осях, полученных путем поворота старых на угол 450 относительно оси 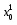 . .Решение. Определим матрицу преобразования декартовых координат – это матрица косинусов углов межу новыми и старыми осями 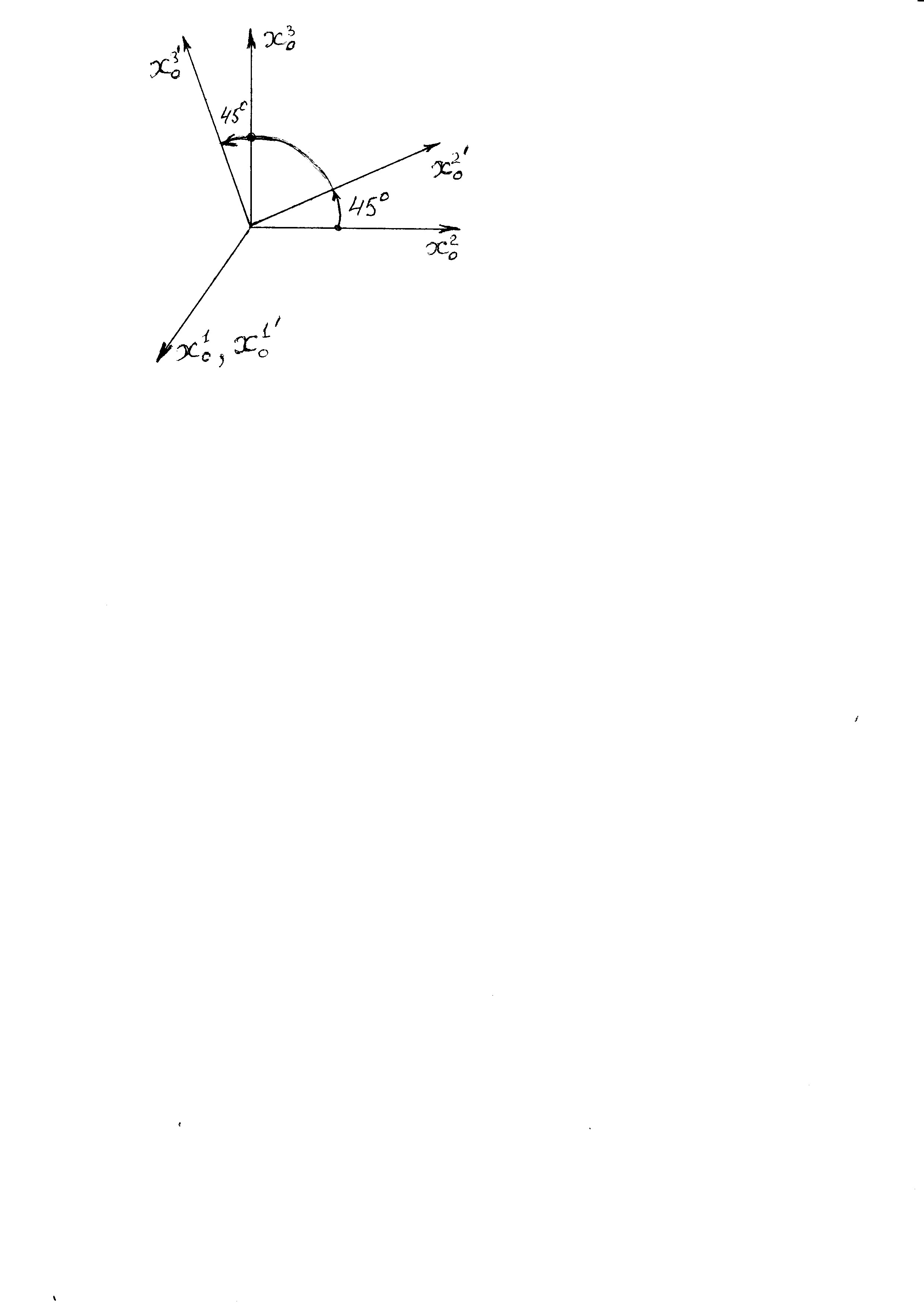 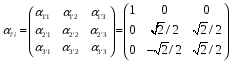 Запишем определение декартового тензора второго ранга 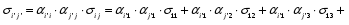 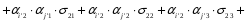 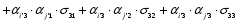 Подставим компоненты тензора в «старых» осях из условия задачи, тогда получим 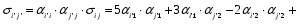 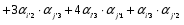 Определим компоненты тензора в «новых» осях 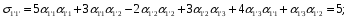 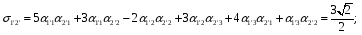 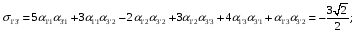 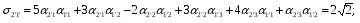 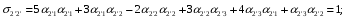 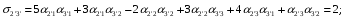 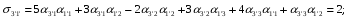 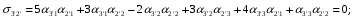 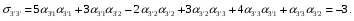 Ответ: 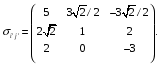 Замечание. В этой задаче важно правильно составить матрицу преобразования декартовых координат при одном повороте относительно других осей  . Следует рассмотреть отдельно углы поворота осей 900 и 1800. . Следует рассмотреть отдельно углы поворота осей 900 и 1800.Тема V. Операции тензорной алгебры Повторим операции, которые можно выполнять над тензорами. 1) Сложение тензоров. В этой операции могут участвовать тензоры одинакового ранга и строения, то есть тензоры с одинаковым числом и чередованием верхних и нижних индексов. В результате мы получаем тензор того же ранга и строения. Тензоры складываются покомпонентно. Например 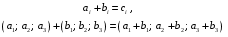 2) Умножение тензора на число. Каждая компонента тензора умножается на это число, в результате получается тензор того же ранга и строения. Например 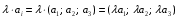 Операция вычитания тензоров выполняется с помощью этих двух операций, т.е. уменьшаемый тензор складывают с вычитаемым умноженным на минус единицу. 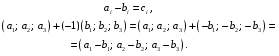 3) Умножение тензоров (внешнее). В этой операции могут участвовать тензоры любого ранга и строения. Каждая компонента одного тензора умножается на каждую компоненту другого тензора, в результате получается тензор, ранг которого равен сумме рангов сомножителей. 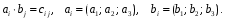 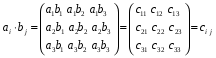 Операция умножения тензоров некоммутативна, т.к. 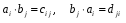 4) Свертка тензора. В этой операции участвуют тензоры, ранг которых не менее двух. Операция заключается в том, что два свободных индекса тензора обозначаются одной буквой, в результате чего становятся индексом суммирования. Ранг тензора уменьшается на две единицы. Тензор нечетного ранга можно последовательно свернуть до тензора первого ранга. Тензор четного ранга можно последовательно свернуть до тензора нулевого ранга. Свертку тензора можно применять к произведению тензоров, тогда это произведение называют внутренним. 5) Перестановка индексов. Если два свободных индекса поменять местами, то мы получим тензор того же ранга, с теми же компонентами, но занумерованными в другом порядке. Например 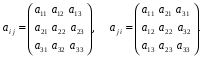 6) Симметрирование тензора. Симметрирование тензора по двум индексам выполняется по формуле 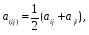 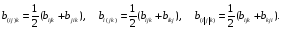 Симметрирование тензора по трем индексам выполняется по формуле 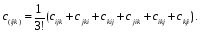 Симметрирование тензора по ‘n’ индексам выполняется по формуле 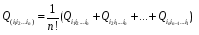 7) Альтернирование тензора (кососимметрирование) Альтернирование тензора по двум индексам выполняется по формуле 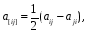 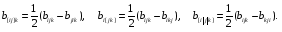 Альтернирование тензора по трем индексам выполняется по формуле 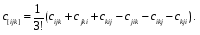 “+” – четная перестановка ijk, “–” – нечетная перестановка ijk. Альтернирование тензора по ‘n’ индексам выполняется по формуле 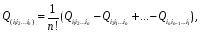 “+” – четная перестановка i1, i2, …,in; “–” – нечетная перестановка i1, i2, …,in. Задача 1. Известен тензор второго ранга 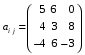 и введены обозначения bij = a(ij), cij = a[ij] Определите следующие выражения: 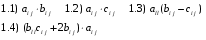 Решение. Определим симметричный и кососимметричный тензоры bij и cij , используя приведенные выше формулы 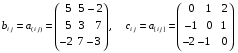 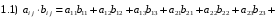 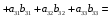 25 + 30 + 20 + 9 + 56 + 8 + 42 + 9 = 199. 25 + 30 + 20 + 9 + 56 + 8 + 42 + 9 = 199.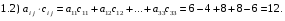 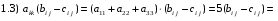 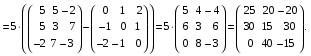 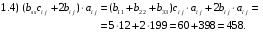 Задача 2. Докажите, что для любого тензора второго ранга aij справедливо равенство 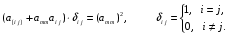 Решение. Предварительно определим следующие тензоры нулевого ранга 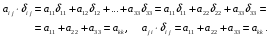 Тогда получим 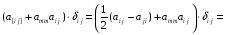 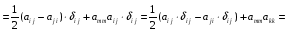 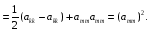 Задача 3. Докажите, что для любого тензора третьего ранга Сijk справедливо равенство 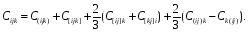 Задача 4. Определите компоненты тензора третьего ранга C[ijk], если известно, что 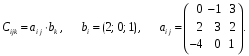 Тема VI. Элементы векторного анализа (дифференциальные операции градиент, дивергенция и ротор в декартовых координатах) Рассмотрим декартову прямоугольную систему координат с ортонорми рованным базисом  Пусть в некоторой области трехмерного евклидова пространства заданы дважды непрерывно дифференцируемое скалярное поле u(M) и векторное поле 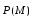 . Тогда grad u и . Тогда grad u и 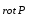 образуют векторные поля, а образуют векторные поля, а 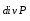 образует скалярное поле. В этом случае возможны пять повторных операций: образует скалярное поле. В этом случае возможны пять повторных операций: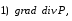  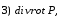 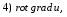 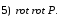 где 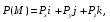 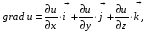 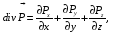 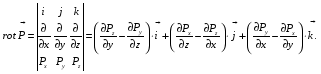 Раскроем повторные операции в общем виде, используя представленные определения. 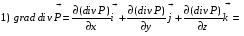 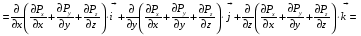 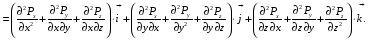 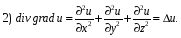 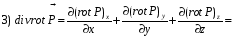 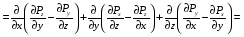 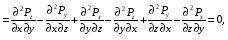 так как смешенные производные не зависят от порядка дифференци рования. 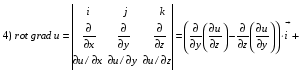 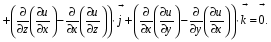 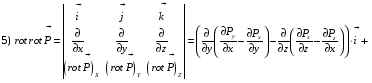 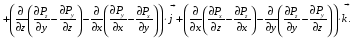 Задача 1. Известно дифференцируемое скалярное поле 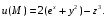 Найдите: 1) grad u, 2) div grad u. Решение. 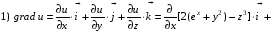 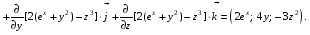 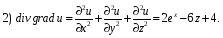 Задача 2. Известны дифференцируемые векторные поля 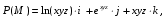 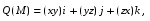 и скалярное поле φ 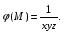 Найдите:  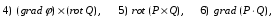  Используйте определение скалярного и векторного произведений 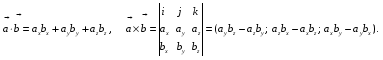 Задачи для домашней контрольной работы ВАРИАНТ 1(контрольное задание к зачету) 1. Определите векторы локального и взаимного базисов сферической системы координат в точке 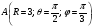 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Даны тензоры первого ранга bi = (1; 2; 3) и di = (–2; 3; –1). Определите: 1.1. [ij]kbidk 1.2. fks = bkds 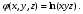 3. Дано векторное поле 3. Дано векторное поле 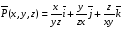 и скалярное поле и скалярное поле Определите  ВАРИАНТ 2 1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 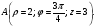 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Докажите, что для произвольного вектора 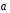 выполняется равенство выполняется равенство 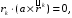 если 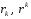 – локальный и взаимный базисы криволинейной системы координат. – локальный и взаимный базисы криволинейной системы координат.3. Составьте выражение 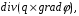 если известно, что если известно, что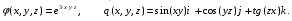 ВАРИАНТ 3 1. Определите векторы локального и взаимного базисов сферической системы координат в точке 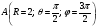 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Составьте выражение d[ij]xj + d(ij)yj , если известно, что xi = (1; -3; 2); yi = (-2; 1; 2) и dij = xiyj 3. По заданному векторному полю 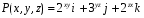 составьте выражение 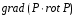 ВАРИАНТ 4 1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 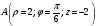 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Определить компоненты тензорных выражений 1.1. a[ij]b(ij) 1.2. amnbns если 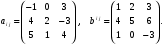 3. Показать, что 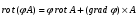 и составить выражение для и составить выражение для 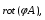 если 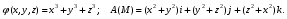 ВАРИАНТ 5 1. Определите векторы локального и взаимного базисов сферической системы координат в точке 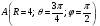 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Определить компоненты тензора d[ij]aj + d(ij)bj , если известно, что ai = (1; 3; –2); bi = (–2; 1; 2) и dij = aibj 3. Составить выражение 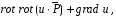 если если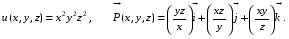 ВАРИАНТ 6 1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 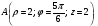 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Определить компоненты тензоров 1.1. ij d(ij) 1.2. ijk d[ij], если dij = xiyj xi = (–1; 2; 4) yi = (3; 2; –3). 3. Составить выражения 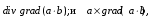 если известно, что если известно, что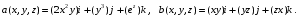 ВАРИАНТ 7 1. Определите векторы локального и взаимного базисов сферической системы координат в точке 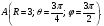 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. В декартовой системе координат задан вектор 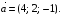 Найдите его ковариантные и контравариантные компоненты в точке М(3; /2; 2) цилиндрической системы координат. Найдите его ковариантные и контравариантные компоненты в точке М(3; /2; 2) цилиндрической системы координат.3. Показать, что 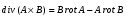 и составить выражение для и составить выражение для 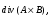 если 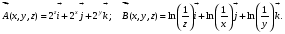 ВАРИАНТ 8 1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 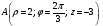 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Определите компоненты тензорных выражений 1.1. d(ij) xiyj1.2.dijij1.3. d[ij] xi Если 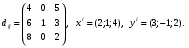 3. По заданным векторным полям 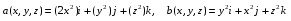 составить выражение для 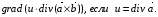 ВАРИАНТ 9 1. Определите векторы локального и взаимного базисов сферической системы координат в точке 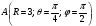 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2.Докажите, что выполняется равенство 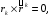 если если 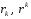 – локальный и взаимный базисы криволинейной системы координат. – локальный и взаимный базисы криволинейной системы координат.3. Покажите, что для любой функции (x, y, z) справедливо равенство rot(grad ) = 0 и составьте выражение Div (grad ), если (x, y, z) = sin(x y z). ВАРИАНТ 10 1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 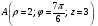 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Разложите тензор 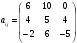 на симметричный (bij) и кососимметричный (dij) и найдите 2.1. aijbij 2.2. ass(bij – dij) 2.3. (brrdij + bij)aij на симметричный (bij) и кососимметричный (dij) и найдите 2.1. aijbij 2.2. ass(bij – dij) 2.3. (brrdij + bij)aij3. Составить выражение 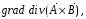 если если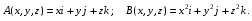 ВАРИАНТ 11 1. Определите векторы локального и взаимного базисов сферической системы координат в точке 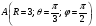 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. В декартовой системе координат задан вектор 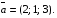 Найдите его ковариантные и контравариантные компоненты в точке А(3; /2; /2) сферической системы координат. Найдите его ковариантные и контравариантные компоненты в точке А(3; /2; /2) сферической системы координат.3. Показать, что 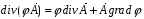 и составить выражение для и составить выражение для 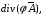 если если 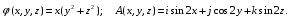 ВАРИАНТ 12 1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 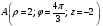 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Определите компоненты тензорных выражений 1.1.d(ij) xiyj1.2.dijij1.3.d[ij] xi Если 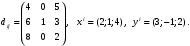 3. По заданным векторным полям 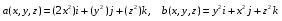 составить выражение для 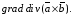 ВАРИАНТ 13 1. Определите векторы локального и взаимного базисов сферической системы координат в точке 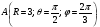 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Даны тензоры первого ранга bi = (3; 2; 1) и di = (–2; 3; –1). Определите: 1.1. i[jk]bidk 1.2. fks = bkds 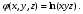 3. Дано векторное поле 3. Дано векторное поле 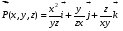 и скалярное поле и скалярное поле Определите  ВАРИАНТ 14 1. Определите векторы локального и взаимного базисов цилиндрической системы координат в точке 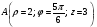 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Докажите, что для произвольного вектора 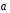 выполняется равенство выполняется равенство 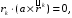 если 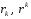 – локальный и взаимный базисы криволинейной системы координат. – локальный и взаимный базисы криволинейной системы координат.3. Составьте выражение 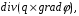 если известно, что если известно, что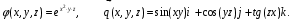 ВАРИАНТ 15 1. Определите векторы локального и взаимного базисов сферической системы координат в точке 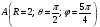 Сделайте рисунок локального базиса. Сделайте рисунок локального базиса.2. Составьте выражение d[ij]xj + d(ij)yj , если известно, что xi = (1; -3; 2); yi = (-2; 1; 2) и dij = xiyj 3. По заданному векторному полю 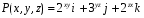 составьте выражение 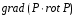 ВОПРОСЫ К ЗАЧЕТУ ОСНОВЫ ВЕКТОРНОГО И ТЕНЗОРНОГО АНАЛИЗА
|
