Скалярное произведение двух векторов и его свойства
 Скачать 73.71 Kb.
|
Скалярное произведение двух векторов и его свойства.Скалярным произведением (или внутренним произведением) 2 векторов есть операция с двумя векторами, итогом чего является число (скаляр), которое не зависит от системы координат и которое характеризует длины векторов-сомножителей и угол между векторами.
Этой операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция зачастую рассматривается как коммутативная и линейная по каждому из сомножителей. Скалярное произведение векторов  , , обозначается так: (порядок записи сомножителей не имеет значения, т.е.  ).Еще используются такие обозначения:  ,  ,  . В основном имеется ввиду, что скалярное произведение определено положительно, т.е.  при каждом  . Если этого не иметь ввиду, то произведение зовется индефинитным (неопределенным).Если хотя бы один из 2 векторов или равен нулевому вектору (равен нулю), то  .Свойства скалярного произведения векторов. 1.  - симметричность.2.  обозначается  и зовется скалярный квадрат.3. Если  , то  4. Если и и  и , то  . Обратное утверждение тоже соответствует действительности.5.  6.  7.  Если же векторы и заданы своими координатами:  ,  , то: скалярное произведение векторов, формула: Формула для определения длины вектора: Длина (модуль) вектора, с известными координатами, равен квадратному корню из суммы квадратов координат. Длина вектора , заданного своими координатами, равна:  Как определить угол между 2 векторами: Как найти угол между двумя векторами 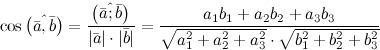, , формула: Ежели угол меж двумя векторами острый, то их скалярное произведение имеет положительный знак; если же угол между двумя векторами тупой, то их скалярное произведение имеет отрицательный знак. Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда эти векторы ортогональны. Альтернативное определение скалярного произведения векторов (вычисление скалярного произведения двух векторов, заданных своими координатами). Вычислить координаты вектора, если заданы координаты его начала и его конца очень просто. Давайте рассмотрим этот вопрос: Пусть есть вектор AB, точка А – это начало вектора, а В - конец, и координаты этих точек приведены ниже: А=(a1,a2,a3), В=(b1,b2,b3) где a1, a2, a3 – координаты точки A b1, b2, b3 – координаты точки B Исходя из этого, координаты вектора АВ: АВ={b1-a1, b2-a2, b3-a3}. Точно так же и в двухмерном пространстве – разница в отсутствии третьих координат. Итак, предположим, даны два вектора, которые заданы набором координат своих точек: а) В двухмерном пространстве (плоскость): 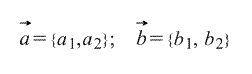 Значит, скалярное произведение этих векторов вычислим по формуле:  б) В трехмерном пространстве: 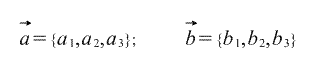 Как и в двухмерном случае, скалярное произведение двух векторов вычисляем по формуле:  Смешанное произведение трех векторов и его свойства Смешанным произведением трех векторов а, b, с называется число, равное скалярному произведению вектора [а; b] на вектор с. Смешанное произведение векторов a, b и с обозначается (а; b; с). Следовательно, (а; b;с) = | [а; b] | • |с| • cos ψ, (1) где ψ - угол между векторами [а; b] и с. Теорема 1. Модуль смешанного произведения трех некомпланарных векторов а, b и с равен объему параллелепипеда, построенного на векторах-множителях. Как известно, площадь S параллелограмма, построенного на векторах а и b, равна | [а; b] |. Поэтому из формулы (1) следует, что (а; b;с) = S • |с | • cos ψ.  С другой стороны, объем V параллелепипеда, построенного на векторах а, b, с (рис. 58), равен произведению площади его основания S на высоту h, причем h = |AA2|, где А2 - проекция вершины А1 на ось, определяемую вектором [а; b]. Так как |AA2| = |с | • cos ψ, то V = S • h = S • | c | • | cos ψ| = | (а; b; с) |. Из формулы (1) видно, что если смешанное произведение трех векторов не равно кулю, то его знак совпадает со знаком cos ψ. Поэтому смешанное произведение положительно, если вектор с направлен в ту же сторону от плоскости векторов а и b, что и вектор [а; b], т. е. если тройка векторов а, b, с правая. Смешанное произведение отрицательно, когда вектор с и вектор [а; b] направлены в противоположные стороны от плоскости векторов а и b, т. е. когда тройка векторов а, b, с левая. Итак, если векторы а, b, с образуют правую тройку, то (а; b;с) > 0, если левую, то (а; b;с) < 0. Теорема 2. Смешанное произведение трех векторов равно нулю тогда и только тогда, когда векторы компланарны. Необходимость. Пусть (а; b, с) = 0. Предположим, что векторы а, b и с некомпланарны. Построим на этих векторах параллелепипед. Его объем V > 0, но по теореме 1 | (а; b;с) | = V, что противоречит предположению. Достаточность. Пусть векторы а, b и с компланарны. Тогда вектор [а; b] перпендикулярен вектору с, но скалярное произведение перпендикулярных векторов равно нулю, т. е. [а; b] • c = (а; b;с) = 0. Рассмотрим некоторые свойства смешанного произведения. 1. Для любых векторов а, b и с справедливы равенства (а; b;с) = (b; с, а) = (с; а; b), т. е. при циклической перестановке множителей смешанное произведение не изменяется. Достаточно доказать первое равенство, так как второе следует из первого. Если векторы а, b и с компланарны, то равенство (а; b;с) = (b; с, а) очевидно; обе части равенства равны нулю. Пусть векторы а, b и с некомпланарны. Тогда в силу теоремы 1 | (a;b;c) | = V и | (b;c;a) | = V, где V - объем параллелепипеда, построенного на данных трех векторах. Но тройки векторов а, b, с и b, с, а являются одновременно либо правыми, либо левыми, поэтому знаки чисел (a;b;c) и (b;c;a) совпадают. 2. Для любых векторов а, b и с справедливы равенства (a;b;c) = - (b; а;с) = - (а; с; b), т. е. при перестановке двух соседних множителей знак смешанного произведения изменяется на противоположный. Первое из равенств следует из свойства векторного произведения: (a;b;c) = [а; b] • с = - [b; а] • с = - (b; а;с). Второе равенство очевидно в силу свойства 1 смешанного произведения. |
