Вопросы по ту.(экзамен) Нагрузки и напряжения. Перемещения и деформации. Тензоры напряжений и деформаций
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
Вопросы по ту.(экзамен) Нагрузки и напряжения. Перемещения и деформации. Тензоры напряжений и деформаций. Виды нагрузок: - временные - постоянные По принципу приложения: - сосредоточенные - распределенные(линейно, поверхностно, объёмно) По характеру воздействия: - статические(величина и место не изменяются или изменяются медленно) - динамические(-//- изменяются быстро) Объемными нагрузками могут быть, например, собственный вес, инерционные силы, силы электромагнитного происхождения и т. д. Поверхностные и массовые нагрузки характеризуются интенсивностями, которые в общем случае зависят от координат х, у, z и выражаются соответственно в Н/м2 (или Па) и Н/м3. Сосредоточенные внешние силы, приложенные в точках поверхности тела, можно рассматривать как предельный случай поверхностных нагрузок, распределенных на малой части поверхности тела. Проекции интенсивности поверхностной нагрузки на координатные оси обозначим рх, ру, рz, а проекции интенсивности массовой нагрузки – X, Y, Z. Проекция интенсивности внешней нагрузки считается положительной, если ее направление совпадает с направлением соответствующей координатной оси. Под действием заданных нагрузок в теле появляются напряжения. Вырежем из рассматриваемого тела элементарный параллелепипед, ребра которого параллельны координатным осям, а их длина равна dx, dy, dz (см. рис. 1.1). На гранях этого параллелепипеда действуют напряжения, которые можно разложить на нормальную составляющую к грани (нормальное напряжение) и касательную (касательное напряжение). В свою очередь, касательное напряжение можно разложить на двесоставляющие, параллельные координатным осям (рис. 1.2). В результате на каждой грани параллелепипеда действуют три напряжения, которые обозначим σxx, τxy, τxz. Примем следующее правило знаков для напряжений: положительные нормальные напряжения являются растягивающими, а отрицательные сжимающими. Нагрузки и напряжения. Перемещения и деформации. Интенсивности напряжений и деформаций. Направляющие косинусы напряжений и деформаций. Виды нагрузок: - временные - постоянные По принципу приложения: - сосредоточенные - распределенные(линейно, поверхностно, объёмно) По характеру воздействия: - статические(величина и место не изменяются или изменяются медленно) - динамические(-//- изменяются быстро) Объемными нагрузками могут быть, например, собственный вес, инерционные силы, силы электромагнитного происхождения и т. д. Поверхностные и массовые нагрузки характеризуются интенсивностями, которые в общем случае зависят от координат х, у, z и выражаются соответственно в Н/м2 (или Па) и Н/м3. Сосредоточенные внешние силы, приложенные в точках поверхности тела, можно рассматривать как предельный случай поверхностных нагрузок, распределенных на малой части поверхности тела. Проекции интенсивности поверхностной нагрузки на координатные оси обозначим рх, ру, рz, а проекции интенсивности массовой нагрузки – X, Y, Z. Проекция интенсивности внешней нагрузки считается положительной, если ее направление совпадает с направлением соответствующей координатной оси. Под действием заданных нагрузок в теле появляются напряжения. Вырежем из рассматриваемого тела элементарный параллелепипед, ребра которого параллельны координатным осям, а их длина равна dx, dy, dz (см. рис. 1.1). На гранях этого параллелепипеда действуют напряжения, которые можно разложить на нормальную составляющую к грани (нормальное напряжение) и касательную (касательное напряжение). В свою очередь, касательное напряжение можно разложить на двесоставляющие, параллельные координатным осям (рис. 1.2). В результате на каждой грани параллелепипеда действуют три напряжения, которые обозначим σxx, τxy, τxz. Примем следующее правило знаков для напряжений: положительные нормальные напряжения являются растягивающими, а отрицательные сжимающими. Интенсивности: Ti=(1/√6)* √(Gx-Gy)2+(Gz-Gy)2+(Gx-Gz)2+6(T2xy+T2zy+T2xz ) Gi=√3*Ti Для главных напряжений Ti =(1/√6)* √(G1-G2)2+(G2-G3)2+(G3-G1)2 Gi=G γi=√2/3((εx-εy)2+(εz-εy)2+(εx-εz)2)+3/2(γ2xy+γ2zy+γ2xz) εi= γi/√3 DG= DG/Ti Dε=2*Dε/γi 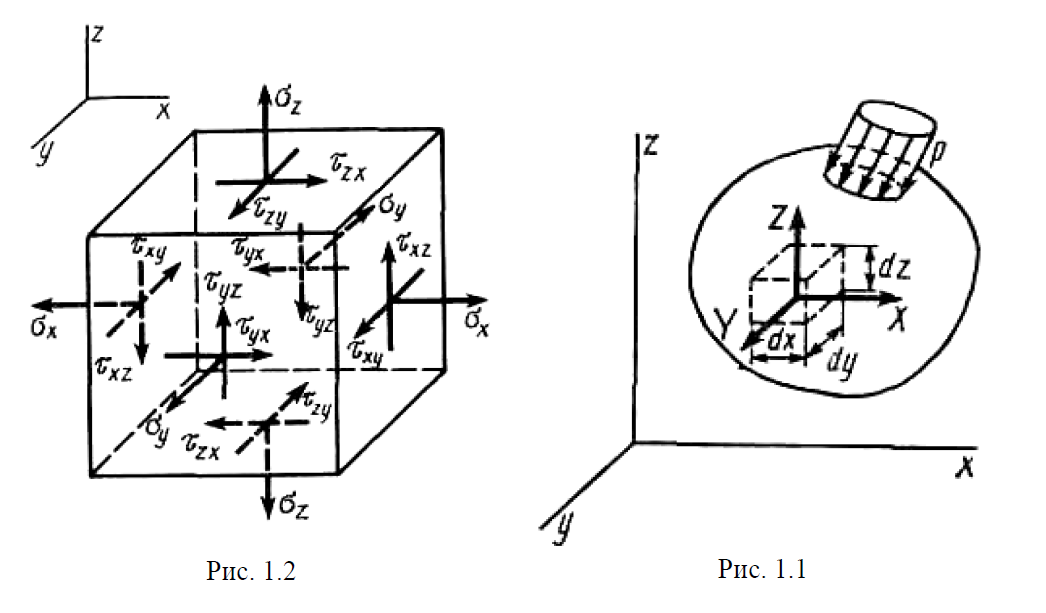 Простое и сложное напряженное состояние. Направляющие косинусы. Главные напряжения и деформации в плоском напряженном состоянии. Экстремальные касательные напряжения. Главные напряжения и деформации в пространственном напряженном состоянии. Экстремальные касательные напряжения. в простр напр сост главными сечениями наз три взаимноперпендикулярных сечения в которых касательные напряжения равны нулю, и действуют только нормальные напряжения. 123- главные напряжения. I1I2I3 0, (1.10) I1 x y z , I2 xy yz zx xy yz zx , x yx zx I3= xy y zy xz yz z Эти коэффициенты являются инвариантными(не зависят от выбора нач. сис. координат) Главным напр соот-ют главные деформации. Они связаны законом Гука. Главное сечение соот- ет главному напряжению сигма i(i=1-3) и находится путем определения направляющих косинусов(li,mi,ni) |(с х – с i)*li+Tyx*mi+Tzx*ni=0 |Txy*li+(c y – c i)+Tzy*ni=0 |li2+mi2+ni2=1 – условие нормировки В сечениях распложенных под углом 45 градусов по отн к главным к напряж действуют экстрем касат напряж T=+-(c i – c j)/2 Постановка задачи теории упругости. Уравнения равновесия (статики) элемента тела. Cx=Mz*y/Jz Постановка задачи т.у. заключается в составлении некоторой системы уравнений описывающей деформирование твердого упругого тела(силовых, кинематических, температурных) Эти уравнения связывают м/у собой объёмные силы и напряж, действ вблизи заданной точки тела. Равновесие бесконечно малого прямоугольного элемента вдоль оси х: Д 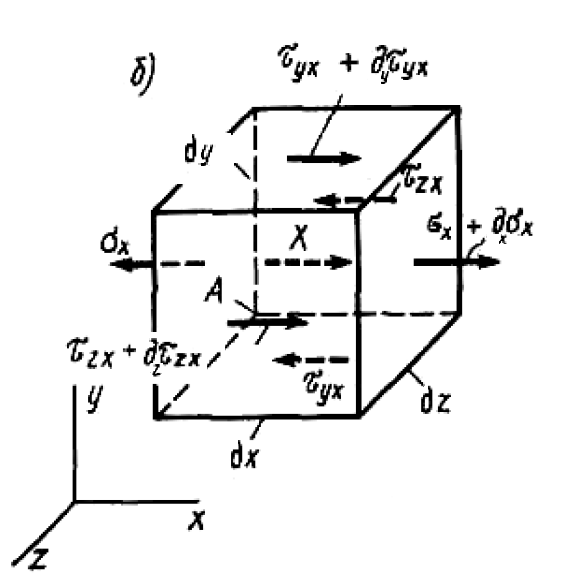 ля этого на гранях элемента будем показывать только напряжения дающие проекции вдоль оси х. Обозначим через X,Y,Z составляющие объёмной нагрузки, действующей на единицу объёма вдоль осей x,y,z соот-но. Примерами объёмной нагрузки является собственный вес и силы инерции. ∑х=0: ∂хGx*dy*dz +∂yTyx*dx*dz +∂zTzx*dy*dx+X*dx*dy*dz=0 Делим ур-е на dx*dy*dz ∂хGx/dх +∂yTyx/dy +∂zTzx/dz+X=0 Постановка задачи теории упругости. Уравнение на поверхности тела. эти уравнения связывают м/у собой поверхностые силы и напряж, действ вблизи заданной точки тела. Вырезается бесконечно малый прямоугольный тетраэдр, при этом наклонная грань его должна быть касательной к поверхности заданной точки. Тс*(l,m,n)=(px,py,pz) П 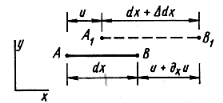 остановка задачи теории упругости. Геометрические уравнения. Эти уравнения связывают между собой перемещения и деформации вблизи заданной точки тела.(уравнения Коши) U+A1B1=AB+U+dxUA1B1-AB=dxUdxU/dx=A1B1-AB/AB => Ex=dU/dx Шесть геометрических уравнений Коши. С помощью них можно решить прямую задачу, т.е. по известным перемещениям найти неизвестные деформации.(обратную решать намного сложнее или невозможно)это связано с тем, что при интегрировании уравнений появляются постоянные функции интегрирования в виде с(х,у) с(у,z) c(z,x) эти постоянные определяются из условия непрерывности перемещений внутри тела и заданных перемещений на поверхности тела. Вывод: таким образом исходные деформации Ех…немогут быть любыми, так как они должны обеспечивать непрерывность перемещений в теле. Постановка задачи теории упругости. Совместные и несовместные деформации. Уравнение совместности деформаций. Деформации, которые позволяют получить непрерывное поле перемещений в теле, называются совместными. В связи с общим требованием к совместности деформаций часто при постановки задачи в т.у. вместо ур-ий Коши исп уравнения совместности деформаций. Эти уравнения получают из уравнений Коши путем исключения из них перемещений. 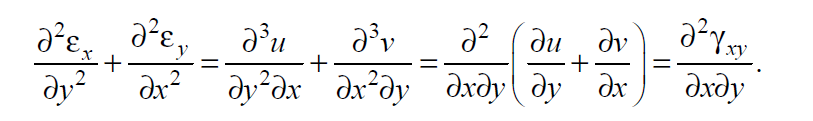 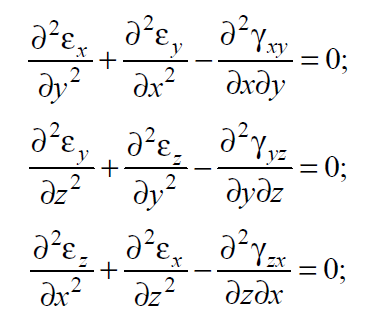 П 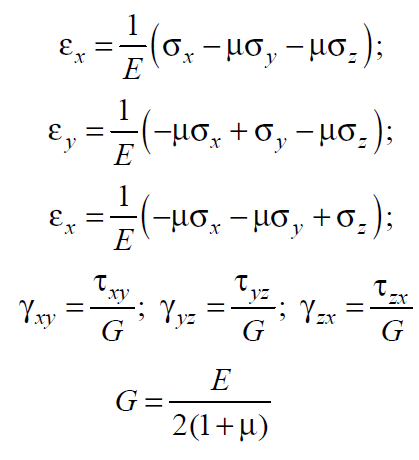 остановка задачи теории упругости. Физические уравнения в прямой форме. Эти уравнения связывают между собой напряжения и деформации вблизи заданной точки тела. Понятие о дифференциале функиции: дифференциалом функции называется линейная часть от полного приращения функции. Если приращение аргумента сделать бесконечно малым, то есть вместо Ах взять dx df=f’(x)dx при этом df будет практически совпадать с полным приращением функции. Дхf=дf*dx/дх Плоское напряженное состояние. Основные уравнения плоской задачи. 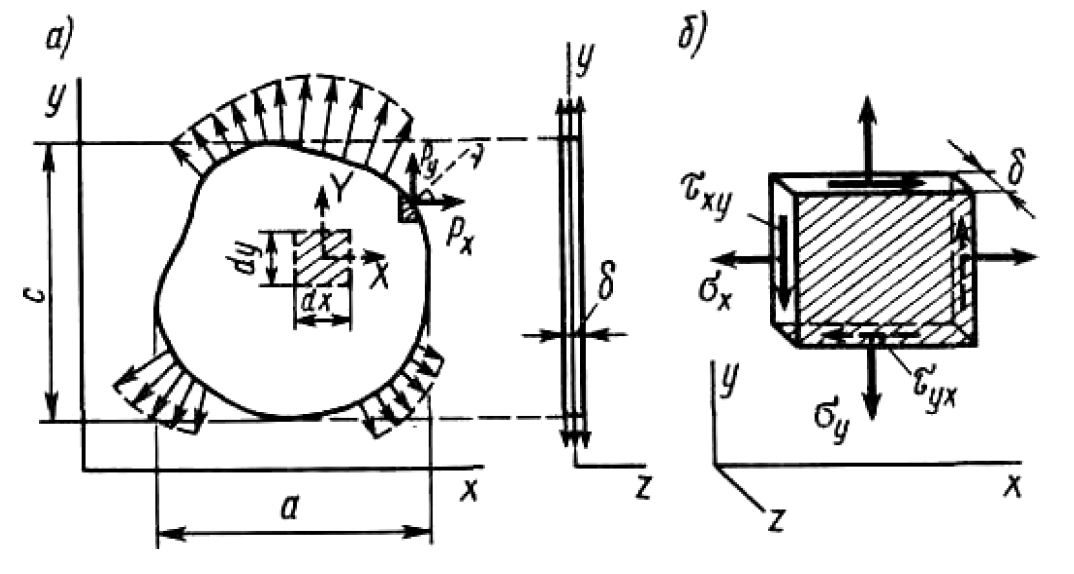 Gx,Gy,Txy,Ex,Ey,Ez,jxy; Gz=Tzy=Tyz=jzx=jyz=0 Уравнения равновесия: ∂хGx/dх +∂yTyx/dy +X=0 ∂хGy/dy +∂yTyx/dx +Y=0 Уравнения на поаерхности: Gх*l +Tyx*m=Px Gy*m +Txy*l=Py Уравнения геометрические: Ех=∂U/∂x Еy=∂V/∂y jxy=∂U/∂y+∂V/∂x Уравнения физические: Ex=1/E(Gx-µGy) E 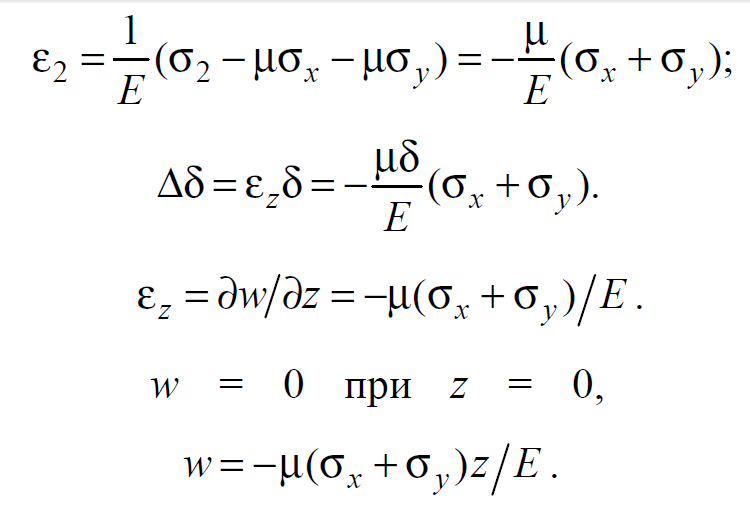 y=1/E(Gy-µGx) jxy=Txy/G И уравнение совместности деформаций Плоская деформация. Основные уравнения плоской задачи. 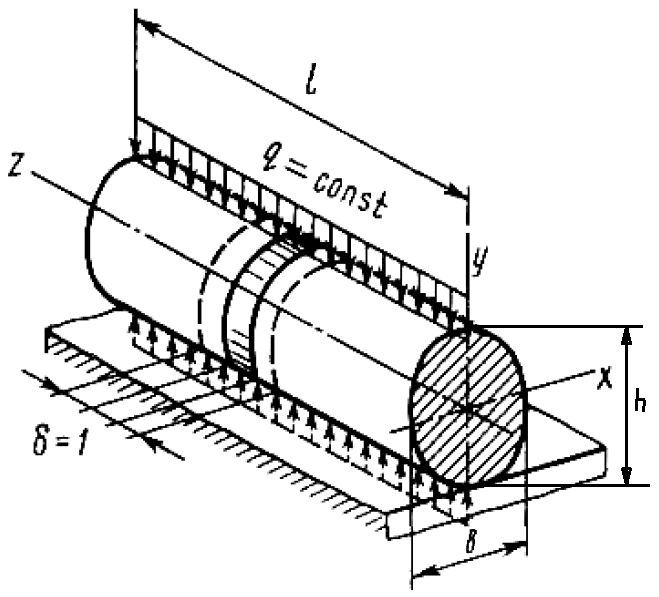 Gx,Gy,Txy,Ex,Ey,Gz,jxy; Ez=Tzy=Tyz=jzx=jyz=0 Все то же самое что и в плоском: статические, геометрические, на поверхности, совмест-деф Физические: Ex=1/E(Gx-µ(Gy+Gz)) Ey=1/E(Gy-µ(Gx+Gz)) 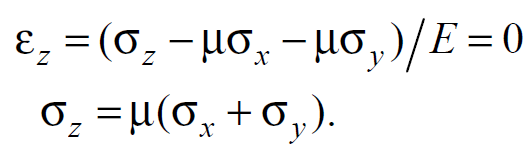 Решение плоской задачи теории упругости с помощью функций напряжений. Rx=S X*dx*δ Rx=S Y*dx*δ М=S (-Y)*x*dx*δ Геометрические уравнения Коши…и интегрирование 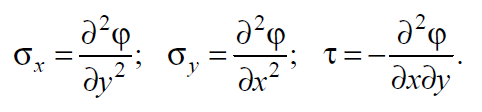 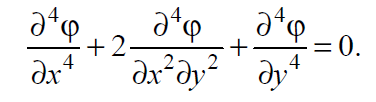 Линейно-упругий, нелинейно-упругий и упругопластичный материалы. Физическая нелинейность. При нагружении выше предела пропорциональности напряжения нелинейно зависят от деформаций. Материал для которого соблюдается закон Гука называется физически линейным, иначе физически нелинейным. Сущ два вида поведения за пределом пропорциональности: - нелинейно-упругий - упруго-пластический НЕЛИНЕЙНО-УПРУГИЙ упруго-пластический 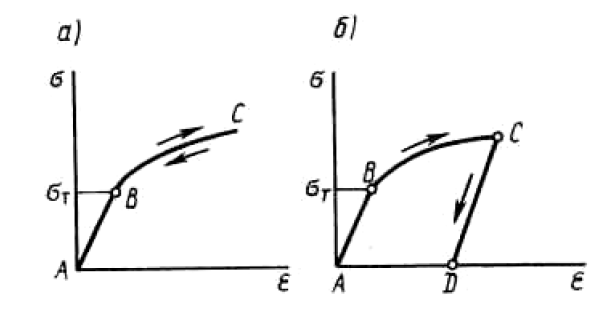 После удаления нагрузки в образце появляются остаточные деформации, подобные материалы называются упругопластическими. А)-разгрузка происходит по линии, кот совпадает с линией первоначального нагружения, это означает, что после полной разрузки полная деформация Ех=0, значит в нелинейно-упругом материале возникают только упругие деформации, которые исчезают после снятия нагрузки. Б)-Еобщ=Еупр+Епл Линия разгрузки не совпадает с первоначальной линией нагружения, разгрузка происходит приблизительно по прямому отрезку, почти параллельному первоначальному линейно-упругому участку. Таким образом в упруго-пластическом материале возникают не только упругие, но и пластические(остаточные) деформации. Для нелинейно-упругого материала всегда сущ однозначная зависимость м/у деформацией и напряжением, т.е. по известной деформации всегда можно единственным способом найти соот-ее напряжение. Для упругопластичного материала нет взаимно однозначной зависимости, если кроме активного нагружения еще имеется разгрузка. Для определения по неизвестной Е* соот-его напряжения G* требуется обязательно знать предысторию деформации материала. Деформирование упругопластического стержня при центральном растяжении-сжатии и плоском изгибе. При этом на испытательном оборудовании записываются диаграммы деформирования образца P-ΔL, или сразу диаграмма деформирования материала G-E (G=P/A0; E=ΔL/L) Постановка задачи и уравнения теории пластичности. Общее и различие с постановкой задачи теории упругости. Теорией пластичности называется раздел механики твердого деформированного тела, в котором изучается определение усилий, перемещений, деформаций, напряжений в пластических телах. В постановку задачи входит составлении некоторой системы уравнений описывающей деформирование твердого деформированного тела(силовых, кинематических, температурных) - статические ур-я - геометрические ур-я Коши - геометрические ур-я совместности деформации - НО ФИЗИЧЕСКИЕ ПРИНЦИПИАЛЬНО ДРУГИЕ НЕЖЕЛИ В Т.У. Механические свойства пластического материала. Физический и условный пределы текучести. Сущ два основных вида пластичного материала: - материал имеющий физическую площадку и предел текучести - материал не имеющий площадку текучести и предела текучести 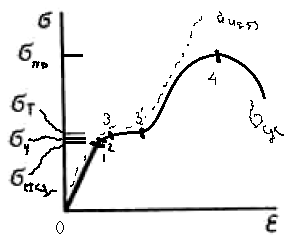 1 – предел пропорциональности(наибольшее условное напряжение, до которого справедлив закон Гука) Gпц=Pпц/А0 2 – предел упругости(условное напряжение, при превышении которого в материале появляются пластические деформации) Gу=Pу/А0 3 – предел текучести(условное напряжение, после которого происходит рост деформации без увеличения нагрузки – начинает течь) Gу=Pу/А0 3’-4 участок упрочнения 4 – предел прочности(наибольшее условное напряжение, которое испытывает образец при испытании до разрушения) Gпч=Pпч/А0 Gисп=P/А0 Gусл=P/А0 Для мат не имеющих физического Gт, исп понятие условного предела текучести. Обычно за условный Gт принимают G0,2 при котором возникают пластические деформации Е=0,2% Активное нагружение и разгрузка. Повторное-попеременное и знакопеременное нагружение. Эффект Баушингера. Если образец сначала нагружают, например растягивают, а затем разгружают, но без перехода в стадию сжатия, а затем опять загружают, то нагружение называется повторно-переменным. Е 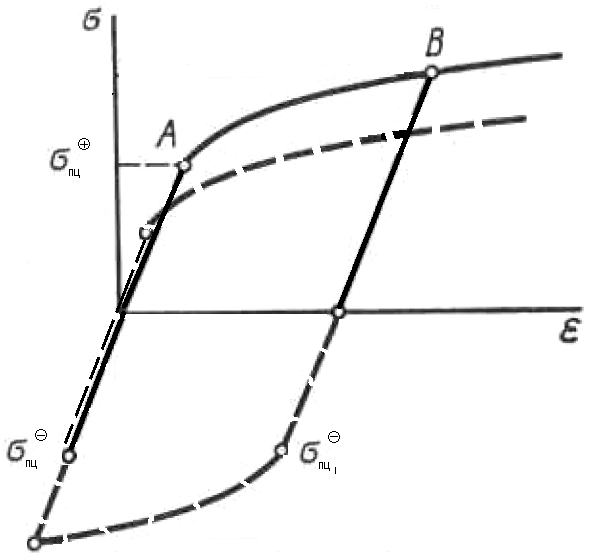 сли образец сначала нагружают, например растягивают, затем полностью разгружают и после этого нагружают нагрузкой обратного знака, т.е. сгружают, то нагружение называется законопеременным. После предварительной пласт деф одного знака, например растяжение, при нагружении обратным знаком например сжатие происходит уменьшение величины предела пропорциональности по сравнению с не деформированным. Этот эффект вызывает мало цикловую усталость материала, при котором за несколько десятков циклов даже при напряжении заметно меньших предела прочности возникает разрушение. Апроксимация диаграмм деформирования материалов и требования к ней. Упругопластическая и жесткопластическая задачи. Апроксимация(приближение): целью является замена реальной, т.е. фактической диаграммы деформации материала G-E на более простую математическую функцию. При этом учитываются основные свойства материала, и в тоже время значительно упрощается решение задачи. При решении задачи-расчета пластического тела обычно рассматривают две модели материала: упругопластический и жесткопластический. Упругопластический материал - это материал, в котором величина упругой деформации сравнима(<10-15 раз)с величиной пласт деформации, поэтому в расчете учитывают не только упругую, но и пластическую деформацию. И 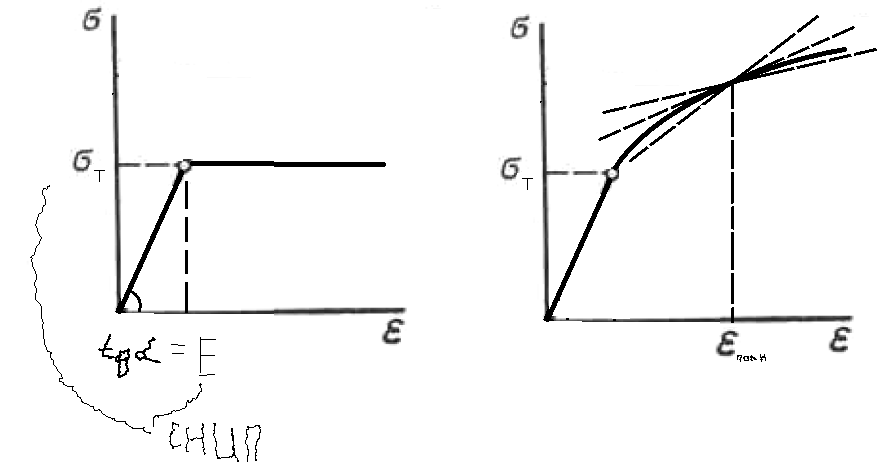 деальная упругопластичная диаграмма Прандтля Упругопластическая диаграмма с линейным упрочнением 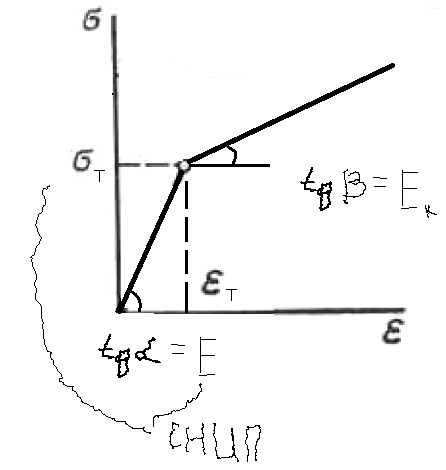 Упругопластическая диаграмма с нелинейным упрочнением Аналог 2 но с упругой площадкой текучести Аналог 3 с площадкой текучести Диаграммы без выраженного линейно-упругого участка(нелинейные): Без выраженного нисходящего участка Нелинейная диаграмма с нисходящим участком(для бетона) Жесткопластичный материал – это материал, в котором величина упругой деф намного меньше пластической, поэтому упругая деф в расчетах не учитывается: Идеальная жесткопластическая диаграмма без упрочнения 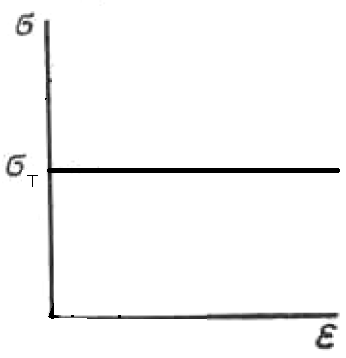 жесткопластическая диаграмма с линейным упрочнением жесткопластическая диаграмма с нелинейным упрочнением Назначение критериев (условий) пластичности. Критерий Треска-Сен-Венана-Леви. Необходимость и достаточность условий пластичности. Причина течения материала считается Tmax вблизи заданной точки. Формулировка: течение материала в сложном напряженном сост наступит тогда, когда Tmax в сложном случае достигнет значения Tmax в простом случае, в момент наступления течения Tmax(слож)=(G1-G3)/2 Tmax(прост)=(Gт-0)/2=Gт/2 Tmax(слож)= Tmax(прост) => (G1-G3)/2=Gт/2 G1-G3= Gт τmaxчист сд=τт, τmaxод.р-с= 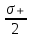 →σт=2τт →σт=2τтНазначение критериев (условий) пластичности. Критерий Губера-Мизеса-Генки. Необходимость и достаточность условий пластичности. Причиной течения материала считается удельная энергия формоизменения. Формулировка: течение материала в СНС наступает тогда, когда удельная энергия формоизменения в СНС станет равной уд.эн. формообразования в ПНС в момент наступления течения. Uф= 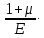 τi2 → Uфпр= τi2 → Uфпр=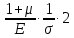 σтi , Uфсл= Uфпр → σтi , Uфсл= Uфпр →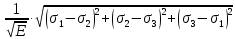 = =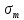 Критерий Мизеса немного лучше подтверждается экспериментами, чем критерий Сен-Венана. Однако в целом считается что они оба занимают равноправное положение. При решении конкретных задач обычно пользуются тем из них, который упрощает решение. Критериев пластичности достаточно для решения задач ТП,если материал не имеет упрочнения (т.е. применяются идеальные упруго-пластичные диаграммы Прендтеля). При наличии упрочнения для решения задач ТП требуется знать соотношение напряжения-деформации при упруго-пластическом деформировании материала. В общем случае эти соотношения зависят не только от текущих значений компонент тензоров напряжений и деформаций, но и от путей их достижений. Простое и сложное нагружение. Теорема А.А.Ильюшина о простом нагружении. Основные типы теорий пластичности и их назначение. В ТП различают два вида нагружения тел: простое и сложное. Нагружение называется простым,если все компоненты тензора напряжений(2 вариант компонент девиатора напряжений) возрастает пропорционально одному параметру. В противном случае нагружение называется сложным. рисПример. Одновременное растяжение и кручение тонкостенной трубы P=λ∙P0,Mx=λ∙Mx0 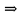 σx,τxy – тоже возрастают пропорционально λ. σx,τxy – тоже возрастают пропорционально λ.При простом нагружении компоненты нагружающего тензора напряжений не зависят от λ,т.е. не меняются.рис Все теории пластичности разделяют на два типа : 1.деформации теории пластичности и 2. Теории пластического течения. Деформационная теория применима только для простого нагружения и для нагружения близкого к простому. В котором устанавливается связь между напряжениями и деформациями(конечные соотношения). Теория пластического течения применима как для простого, так и для сложного нагружения. В ней используются соотношения между напряжениями и бесконечно малыми приращениями пластических деформаций (дифференциальные соотношения). Понятие о теории малых упругопластических деформаций А.А.Ильюшина. Гипотезы. Одной из самых распространенных и известных деформационных теорий является теория малых упругопластических деформаций А.А.Ильюшина для изотропного тела. В ее основе лежат следующие гипотезы, вытекающие из обобщения экспериментальных данных. Гипотеза изменения объема. При упругопластическом деформировании объемная деформация считается упругой и подчиняется закону Гука. 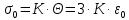 , , 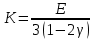 - модуль упругости при изменении объема. - модуль упругости при изменении объема.Гипотеза изменения формы. При упругопластическом деформировании направляющие тензоры напряжений и деформаций равны. 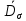 = =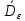 Получим отсюда соотношения между напряжениями и деформациями 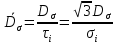 ; ; 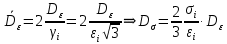 Или покомпонентно: 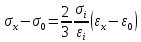 , , 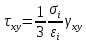 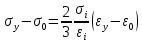 , , 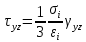 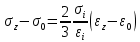 , , 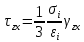 Отсюда используя 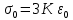 можно выразить напряжения можно выразить напряжения 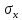 , ,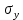 , ,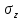 через деформации через деформации 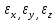 и наоборот. и наоборот.В частном случае при линейно-упругом деформировании из соотношений получатся обобщенный закон Гука Интенсивность напряжений 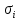 при активном упругопластическом деформировании является вполне определенной функцией интенсивности деформаций при активном упругопластическом деформировании является вполне определенной функцией интенсивности деформаций 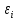 для данного материала и не зависит от вида напряженного состояния для данного материала и не зависит от вида напряженного состояния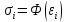 |
