Контрольная работа «Векторная алгебра». Контрольная работа Векторная алгебра
 Скачать 52.3 Kb. Скачать 52.3 Kb.
|
|
Контрольная работа «Векторная алгебра» 1. Даны точки А, В и С. Разложить вектор a по ортам 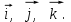 Найти длину, направляющие косинусы и орт вектора a. Найти длину, направляющие косинусы и орт вектора a.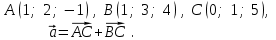 Найдем координаты векторов: 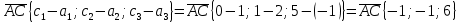 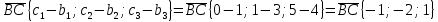 Тогда вектор a по ортам 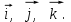 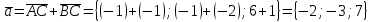 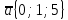 Длина вектора находится по формуле 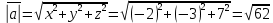 направляющие косинусы равны 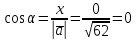 ; ; 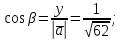 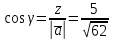 Орт вектора 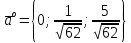 2. Найти косинус угла, образованного вектором 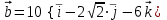 и осью OZ. и осью OZ.Угол между векторами вычисляется по формуле: 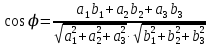 Направляющий вектор оси OZ: (0,0,1) Тогда 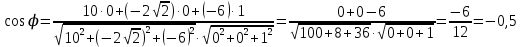 Значение косинуса -0,5 соответствует углу -60 или 120 градусов. 3. Определить, при каком значении m векторы 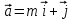 и и 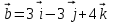 перпендикулярны. перпендикулярны.Найдем скалярное произведение векторов а и b: 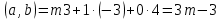 Векторы перпендикулярны, если их скалярное произведение равно нулю. Приравниваем к нулю произведение (а, b): 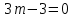 ; ; 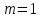 Ответ: При m=1 векторы перпендикулярны 4. Найти вектор х, коллинеарный вектору 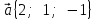 и удовлетворяющий условию х*а=3 и удовлетворяющий условию х*а=3Скалярное произведение двух векторов определяется как произведение длин этих векторов на косинус угла между ними. 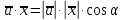 Поскольку векторы коллинеарные, то угол α между ними 0 градусов, т. е 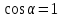 , а вектор , а вектор 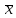 имеет координаты (2k; 1k; (-1)k), где k - коэффициент пропорциональности. имеет координаты (2k; 1k; (-1)k), где k - коэффициент пропорциональности.Тогда 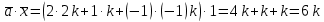 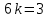 ; ; 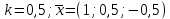 5. Найти площадь треугольника с вершинами 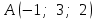 , , 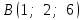 , ,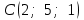 (средствами векторной алгебры). Площадь треугольника, построенного на двух векторах равна половине модуля векторного произведения этих векторов: 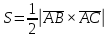 Найдем вектора по координатам точек: 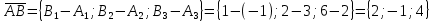 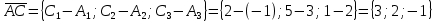 Найдем векторное произведение векторов: 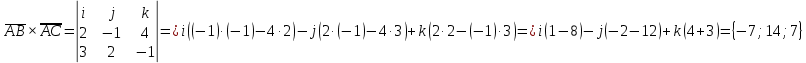 Найдем длину (модуль) вектора: 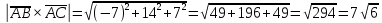 Найдем площадь треугольника: 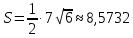 6. Найти объем треугольной пирамиды, построенной на векторах 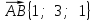 , ,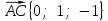 и и 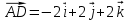 . .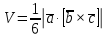 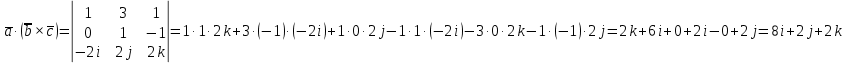 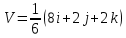 7. Даны координаты вершин пирамиды ABCD. Требуется найти: 1) длины векторов 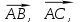 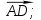 2) угол между векторами 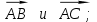 3) площадь грани АВС ; 4) объем пирамиды ABCD.
1) длины векторов 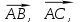 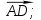 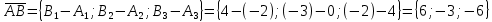 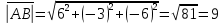 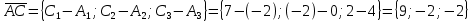 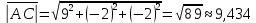 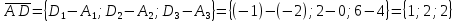 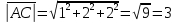 2) угол между векторами 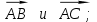 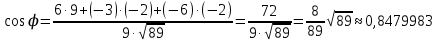 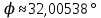 3) площадь грани АВС ; 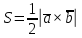 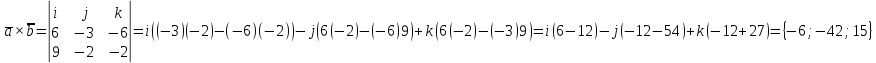 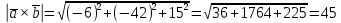 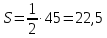 4) объем пирамиды ABCD. 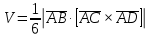 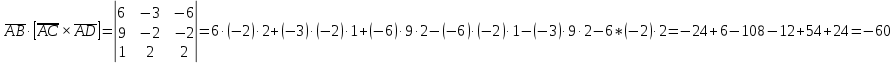 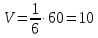 |

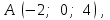
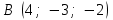 ,
,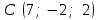 ,
,