Расчет траектории неуправляемых реактивных ЛА малой дальности.. Ход работы Система дифференциальных уравнений Начальные данные
 Скачать 58.3 Kb. Скачать 58.3 Kb.
|
|
Цель работы: Научиться решать систему дифференциальных уравнений методами Рунге-Кутты и Эйлера Ход работы: Система дифференциальных уравнений: 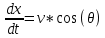 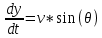 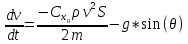 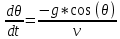 Начальные данные: 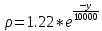 ; ;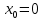 ; ;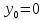 ; ;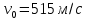 ; ;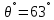 ; ;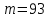 кг; кг;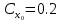 ; ;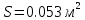 ; ;Теоретическое описание математических методов: Оба метода (Эйлера и Рунге-Кутта) являются итерационными, используются для численного решения системы дифференциальных уравнений. Метод Эйлера имеет первый порядок точности. Формула итерационного процесса выглядит так: 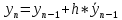 Производная у на каждом шаге интегрирования принимается постоянной, равной значению у в начале каждого шага. Таким образом начальная интегральная кривая, проходящая через точку (x0,y0) заменяется ломаной. Несмотря на недостаточную точность, применяется часто в силу простоты. Метод Рунге-Кутта 4 порядка - более точный и более трудоемкий метод, основанный на аппроксимации искомой интегральной кривой соприкасающейся параболой. Пусть 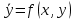 , тогда , тогда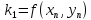 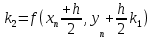 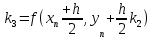 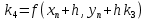 Тогда формула итерационного процесса: 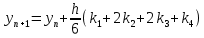 Таблица результатов дальности при вычислениях данными методами:
Вывод: в ходе лабораторной работы был получен навык решения системы дифференциальных уравнений методами Эйлера и Рунге-Кутта 4 порядка, разработана программа по построению траектории полёта неуправляемого снаряда с учётом силы сопротивления и без этого учёта. 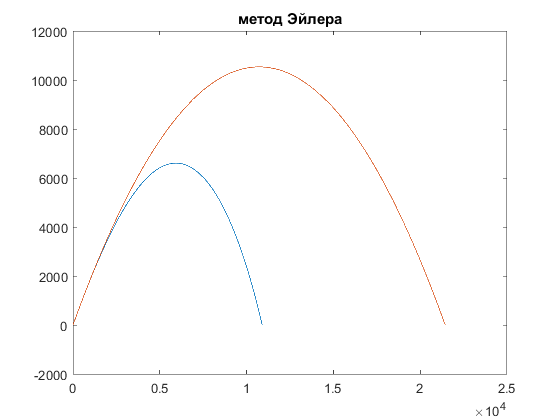 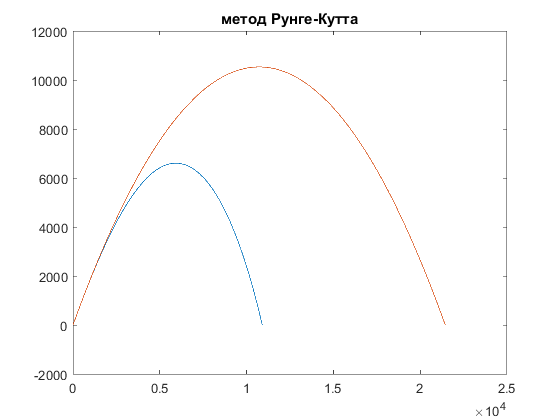 x(1) = 0; y(1) = 0; v(1) = 515; tetta(1) = 1.1; po(1) = 1.22*exp(-y(1)/10000); m = 93; cx = 0.2; s = 0.053; h = 0.01; a = 1; t(1) = h; n = 1; while y(n)>0 | (a == 1) a = 0; po(n) = 1.22*exp(-y(n)/10000); dx(n) = v(n)*cos(tetta(n)); dy(n) = v(n)*sin(tetta(n)); dv(n) = -(cx*po(n)*v(n)*v(n)*s)/(2*m) - 10*sin(tetta(n)); dtetta(n) = -10*cos(tetta(n))/v(n); x(n+1) = x(n)+h*dx(n); y(n+1) = y(n)+h*dy(n); v(n+1) = v(n)+h*dv(n); tetta(n+1) = tetta(n)+h*dtetta(n); t(n+1) = t(n)+h; n = n+1; end xf(1) = 0; yf(1) = 0; vf(1) = 515; tettaf(1) = 1.1; po(1) = 1.22*exp(-yf(1)/10000); m = 93; cx = 0.2; s = 0.053; t(1) = h; a = 1; n = 1; while yf(n)>0 | (a == 1) a = 0; dx(n) = v(n)*cos(tetta(n)); dy(n) = v(n)*sin(tetta(n)); dv(n) = - 10*sin(tetta(n)); dtetta(n) = -10*cos(tetta(n))/v(n); xf(n+1) = xf(n)+h*dx(n); yf(n+1) = yf(n)+h*dy(n); v(n+1) = v(n)+h*dv(n); tetta(n+1) = tetta(n)+h*dtetta(n); t(n+1) = t(n)+h; n = n+1; end figure(1); plot(x, y); hold on plot(xf, yf); title('метод Эйлера'); xr(1) = 0; yr(1) = 0; vr(1) = 515; tettar(1) = 1.1; po(1) = 1.22*exp(-yr(1)/10000); m = 93; Cx = 0.2; s = 0.053; t(1) = h; n=1; while (yr(n)>=0) ro=1.22*exp(-yr(n)/10000); k1x=vr(n)*cos(tettar(n)); x1=xr(n)+(h/2)*k1x; k1y=vr(n)*sin(tettar(n)); y1=yr(n)+(h/2)*k1y; k1v=((-Cx*ro*s*vr(n)^2)/(2*m)-10*sin(tettar(n))); v1=vr(n)+(h/2)*(k1v); k1tetta=(-10*cos(tettar(n))/vr(n)); tetta1 = tettar(n)+(h/2)*k1tetta; ro1=1.22*exp(-y1/10000); k2v=(-Cx*ro1*s*v1^2)/(2*m)-10*sin(tetta1); v2=vr(n)+(h/2)*(k2v); k2x=v1*cos(tetta1); x2=xr(n)+(h/2)*k2x; k2y=v1*sin(tetta1); y2=yr(n)+(h/2)*k2y; k2tetta=(-10*cos(tetta1)/v1); tetta2 =tettar(n)+(h/2)*k2tetta; ro2=1.22*exp(-y2/10000); k3v=(-Cx*ro2*s*v2^2)/(2*m)-10*sin(tetta2); v3=vr(n)+h*(k3v); k3tetta=(-10*cos(tetta2)/v2); tetta3=tettar(n)+h*k3tetta; k3x=v2*cos(tetta2); x3=xr(n)+h*k3x; k3y=v2*sin(tetta2); y3=yr(n)+h*k3y; ro3=1.22*exp(-y3/10000); k4v=(-Cx*ro3*s*v3^2)/(2*m)-10*sin(tetta3); k4tetta=(-10*cos(tetta3)/v3); k4x=v3*cos(tetta3); k4y=v3*sin(tetta3); vr(n+1) = vr(n)+(k1v+2*k2v+2*k3v+k4v)*h/6; tettar(n+1) = tettar(n)+(k1tetta+2*k2tetta+2*k3tetta+k4tetta)*h/6; xr(n+1) = xr(n)+(k1x+k2x*2+k3x*2+k4x)*h/6; yr(n+1) = yr(n)+(k1y+k2y*2+k3y*2+k4y)*h/6; t(n+1) = t(n)+h; n = n+1; end; disp('Рунге, дальность с Х'); k = n-10; while(k disp(t(k)); k = k+1; end yfr(1) = 0; xfr(1) = 0; vfr(1) = 515; tettafr(1) = 1.1; n = 1; t(1) = h; while (yfr(n)>=0) k1x=vfr(n)*cos(tettafr(n)); x1=xfr(n)+(h/2)*k1x; k1y=vfr(n)*sin(tettafr(n)); y1=yfr(n)+(h/2)*k1y; k1v=-10*sin(tettafr(n)); v1=vfr(n)+(h/2)*(k1v); k1tetta=(-10*cos(tettafr(n))/vfr(n)); tetta1 = tettafr(n)+(h/2)*k1tetta; k2v=-10*sin(tetta1); v2=vfr(n)+(h/2)*(k2v); k2x=v1*cos(tetta1); x2=xfr(n)+(h/2)*k2x; k2y=v1*sin(tetta1); y2=yfr(n)+(h/2)*k2y; k2tetta=(-10*cos(tetta1)/v1); tetta2 =tettafr(n)+(h/2)*k2tetta; k3v=-10*sin(tetta2); v3=vfr(n)+h*(k3v); k3tetta=(-10*cos(tetta2)/v2); tetta3=tettafr(n)+h*k3tetta; k3x=v2*cos(tetta2); x3=xfr(n)+h*k3x; k3y=v2*sin(tetta2); y3=yfr(n)+h*k3y; k4v=-10*sin(tetta3); k4tetta=(-10*cos(tetta3)/v3); k4x=v3*cos(tetta3); k4y=v3*sin(tetta3); vfr(n+1) = vfr(n)+(k1v+2*k2v+2*k3v+k4v)*h/6; tettafr(n+1) = tettafr(n)+(k1tetta+2*k2tetta+2*k3tetta+k4tetta)*h/6; xfr(n+1) = xfr(n)+(k1x+k2x*2+k3x*2+k4x)*h/6; yfr(n+1) = yfr(n)+(k1y+k2y*2+k3y*2+k4y)*h/6; t(n+1) = t(n)+h; n = n+1; end; figure(2); plot(xr, yr); hold on plot(xfr, yfr); title('метод Рунге-Кутта'); | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
