Ход урока.
Закрепление материала прошлого урока – 7 минут

Под буквой а) ученик решает у доски.
Изучение нового материала – объяснение материала – 15 минут.
Изучение теории на странице 155 – 156 учебника:
Всякое положительно число А можно записать так
А=а*10k
где а удовлетворяет неравенствам 1≤а≤10, k – целое число. Такую запись называют записью числа в стандартном виде. Показатель степени k здесь может быть любым целым числом – положительным, отрицательным, нулем; число 10k называют порядком числа А.
Например
273,095=2,73095*102
0,21=2,1*10-1
0, 0234=2,34*10-2
3,1=3,1*100
В правых частях равенств записаны числа в стандартном виде.
Задание. Как можно записать в стандартном виде следующие числа?
0,0021 // 2,1*10-3
0,2346 // 2,346*10-1
126,528 // 1,26528*102
258963,2589 // 2,589632589*105
203,049 // 2,03049*102
Кто помнит, что такое значащая цифра? // Напомни, что значащей цифрой называют его первую (слева на право) отличную от нуля цифру, а также все следующие за ней цифры.
Из этих примеров видно, что для приведения числа стандартному виду надо перенести в нем запятую так, чтобы она оказалась непосредственно правее первой значащей цифры, и полученное число умножить на 10k, где k подбирается так, чтобы произведение было равно данному числу.
При решении многих задач цифры округляются до первой, второй или третьей и.т.д значащей цифры. Числа а в записи округляют с точностью, которая необходима в данной задаче, и тогда равенство А=а*10k заменяют на приближенное равенство.
Округлим пример до первой, второй и третьей значащей цифры.
2, 99792460*108 ≈ 3*108
2, 99792460*108 ≈ 3,0*108
2, 99792460*108 ≈ 3,00*108
2, 99792460*108 ≈ 2,998*108
Если значимая цифра меньше 5, то цифру отбрасывают и вместо ее ставят 0. Если значимая цифра 5 и больше, то эту цифру отбрасывают и вместо нее ставят 0, а к предыдущую цифру увеличивают на единицу.
Вы помните какое число называется числом в периоде?
Числом в периоде называется число вида: 2,34(5) =2,3455555……
При приближенном умножении и делении чисел надо округлять сами числа и результат вычислений с точностью до одной и той же цифры. Если же записать цифры в стандартном виде, то округление чисел и результата вычислений с нужной точностью только упроститься. Это видно из следующего примера:

Закрепление изученного материала – 16 минуты.
Из учебника выполняем задания
Работа у доски
№603 (а, д, и, б, е, к), №605 (а, в, д, ж), №606 (а, б, в, г, д), №607(а, в, д, ж).
Учащиеся выходят к доске по цепочке.
Итог урока – 2 минуты.
Выставление оценок.
Домашнее задание: №603 (в, ж, л, г, з, м), №605 (б, г, е, з), №606 (е, ж, з, и, к, л, м), №607(б, г, е, з), №608.
1. Вводное слово учителя.
Стремление постичь тайны времени, пространства и своё место во Вселенной издавна не давало покоя человеку. Вот и сегодня, как отмечает известный писатель-фантаст Е. И. Парнов, человек снова «стоит на перекрёстке бесконечностей. Одна дорога уводит его в мир галактик, туда, где разлетающееся вещество достигает почти световых скоростей, другая — в микромир с исчезающе малыми масштабами расстояний и длительностей...». И уже несколько тысячелетий, не зная покоя, человеческая мысль блуждает по этим дорогам.
Отправной точкой в её странствиях всегда была Земля. Диаметр нашей планеты составляет около 12 800 км, Солнца — в 109 раз больше. Если представить себе Землю в виде крупинки размером 1 мм, то диаметр Солнца окажется равным примерно 11 см. При этом Земля (в выбранном масштабе) будет двигаться вокруг светила по орбите радиусом чуть меньше 12 м. Диаметр же всей Солнечной системы превысит 900 м!
Выйдем за её пределы. Ближайшая к Солнцу звезда Проксима Кентавра находится от нас на расстоянии, почти в 7 тыс. раз превышающем радиус Солнечной системы. Чтобы преодолеть такой путь, свету требуется более четырёх лет. Если же выразить это расстояние в километрах, получится 14-значное число. Космическая станция, движущаяся с третьей космической скоростью (16,67 км/с), доберётся до неё не ранее чем за 70 тыс. лет! А ведь это наша ближайшая «соседка», остальные звёзды расположены ещё дальше.
Обратим теперь свой взгляд в обратную сторону — ту, которая уводит нас в глубь материи.
Атомы настолько малы, что их нельзя увидеть ни в один оптический микроскоп. По своим размерам (примерно 1010 м) они во столько же раз меньше обыкновенного яблока, во сколько раз яблоко меньше земного шара. А число атомов в яблоке так же велико, как и число звёзд в наблюдаемой Вселенной.
Сегодня будем продолжать работать с такими числами и записывать их в интересном виде. Как он называется? - Стандартный вид числа. – Верно. Это и есть наша тема.
II. Актуализация опорных знаний
В науке и технике астрономы, физики, химики, биологи ставят эксперименты, затем исследуют получившиеся результаты и получают очень большие и очень малые числа.
Прослушаем сообщения о связи математики с этими науками.
(Алина и Михаил – доклады по метапредметным связям, Полина, Дима – по нанотехнологиям).
III. Повторение нового материала
Математики в своем научном творчестве часто помогают им решать различные задачи, используя теорию больших и малых чисел.
Например, большим числом выражается масса Земли – 5 980 000 000 000 000 000 000 т.
(5 секстиллионов 980 квинтиллионов т).
Давайте с помощью таблицы его прочитаем.
На слайде - таблица названий больших чисел.
МИЛЛИОН – 6
МИЛЛИАРД – 9
ТРИЛЛИОН – 12
КВАДРИЛЛИОН – 15
КВИНТИЛЛИОН – 18
СЕКСТИЛЛИОН – 21
СЕПТИЛЛИОН – 24
ОКТИЛЛИОН – 27
НОНИЛЛИОН – 30
ДЕЦИЛЛИОН – 33
Как вы думаете как может называться число у которого 100 нулей? (гугол)
Малым числом выражается размер вируса гриппа равен 0, 000000103 м. (нуль целых, сто три миллиардных м).
Вывод: мы видим, что читать такие числа и выполнять над ними какие-либо действия очень сложно.
– Известна ли вам более удобная форма записи больших и малых чисел?
– Формулирование целей урока (вместе с учениками)
– Обратимся к помощи учебника, п. 8.3 (стр.155).
Задание. Прочтите текст учебника и ответьте на вопросы (вопросы на слайде). Занесите информацию в тетрадь для правил.
– Какая запись называется стандартным видом числа?
– Как называется число n в этой записи?
– Что показывает большой положительный порядок в стандартной записи числа?
– Какая цифра числа называется значащей?
3. Алгоритм записи числа в стандартном виде
Составим алгоритм записи числа в стандартном виде. По учебнику п. 8.3 (стр.155).
( формулируем этапы алгоритма)
Алгоритм записи числа в стандартном виде
1. Поставить в данном числе запятую правее первой значащей цифры.
2. Полученное число умножить на 10 в степени n.
3. Степень n подобрать так, чтобы произведение было равно данному числу .
IV. Закрепление изученного материала
(задания на слайде)
1. Можно ли про следующие числа сказать, что они записаны в стандартном виде:
 ; ;  ; ; 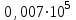 . .
2. Представьте в стандартном виде числа:
350, 72000 , 0, 026, 0, 00000905.
3. Запишите в стандартном виде числа: (ответы – на доску)
а) масса атома кислорода 0, 000 000 000 000 000 000 000 02662 г;
б) толщина пленки мыльного пузыря 0,000 000 06 см;
в) диаметр молекулы воды 0,000 000 03 см;
г) расстояние до туманности Андромеды 95 000 000 000 000 000 000 км;
д) толщина человеческого волоса равна 0,00007 м;
е) масса Солнца равна 1 983 000 000 000 000 000 000 000 000 000 кг.
(прокомментировать решение).
4. Дифференцированная работа с учащимися.
1 группа – ученики, успешно справившиеся с заданиями, дальше самостоятельно работают с учебником. Задание для них проецируется на экране:
Ответьте на вопрос: как выполняется умножение и деление чисел, записанными в стандартном виде? ( слайд)
1. Выполните действия:
а) (3,5 · 10-7) · (3 · 10-5 )= (3,5 · 3) · (10-7 · 10-5) = 10,5 · 10-12 = 1,05 · 10 · 10-12 =
=1,05 · 10-11.
б)  . .
(сначала проецируется задание, затем для проверки – решение)
2. Самостоятельно номер 607(1 столбик) в учебнике.
2 группа – это ученики, испытывающие затруднения при решении заданий, они работают с учителем , выполняя задание, записанное на доске:
1. Представить числа в стандартном виде:
67; 0, 0027; 29,54; 0,000087; 95 000 000. |
 Скачать 455.36 Kb.
Скачать 455.36 Kb.


 ;
;  ;
; 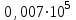 .
. .
.