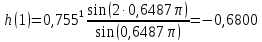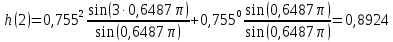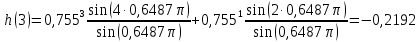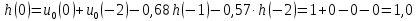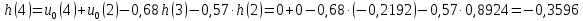Контрольная работа. Холодилин Александр Евгеньевич Проверил Чернокозов Владимир Васильевич Москва, 2020 Цель выполнения контрольной работы исследование
 Скачать 220.01 Kb. Скачать 220.01 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»  Факультет: «Машиностроение». Кафедра: «Автоматика и управление». Дисциплина: «Математические основы дискретных систем». Контрольная работа. Вариант 65. Группа 181-251 Выполнил: Холодилин Александр Евгеньевич Проверил: Чернокозов Владимир Васильевич Москва, 2020 Цель выполнения контрольной работы: исследование рекурсивного звена 2-го порядка во временной области, z-области и частотной области. Задание на контрольную работу: 1. Записать передаточную функцию (ПФ). 2. Записать разностное уравнение (РУ). 3. Изобразить структурную схему. 4. Записать формулу импульсной характеристики (ИХ) с учетом нулевых начальных условий. 5. Рассчитать 5 отсчетов ИХ по полученной формуле. 6. Рассчитать 5 отсчетов ИХ с помощью РУ. 7. Сравнить результаты вычислений пп. 5, 6. 8. Построить график ИХ (5 отсчетов). 9. Изобразить карту нулей и полюсов. 10. Записать формулы для расчета АЧХ и ФЧХ в произвольной точке. 11. Сделать вывод о качественном характере АЧХ и ФЧХ по карте нулей и полюсов. 12. Выполнить экспресс-анализ АЧХ и ФЧХ. 13. Построить графики АЧХ и ФЧХ по результатам пп. 11–12. Исходные данные(Вариант 65)– коэффициенты ПФ H(z) 2-го порядка: b0 = 1; b1= 0; b2= 1; a1= 0,68; a2= 0,57. Решение 1. Запишем ПФ на основе ее общего вида (1.49)  (3.1а) (3.1а)Исследуемое звено не является базовым. 2. Используя методику п. 1.4.3, на основе РУ общего вида (1.50) получаем y(n) = x(n) + x(n − 2) − 0,68 y(n −1) − 0,57y(n − 2) . (3.2а) 3. На основе структурной схемы рекурсивного звена 2-го порядка общего вида (рис. 1.20) имеем схему рис. 3.5. 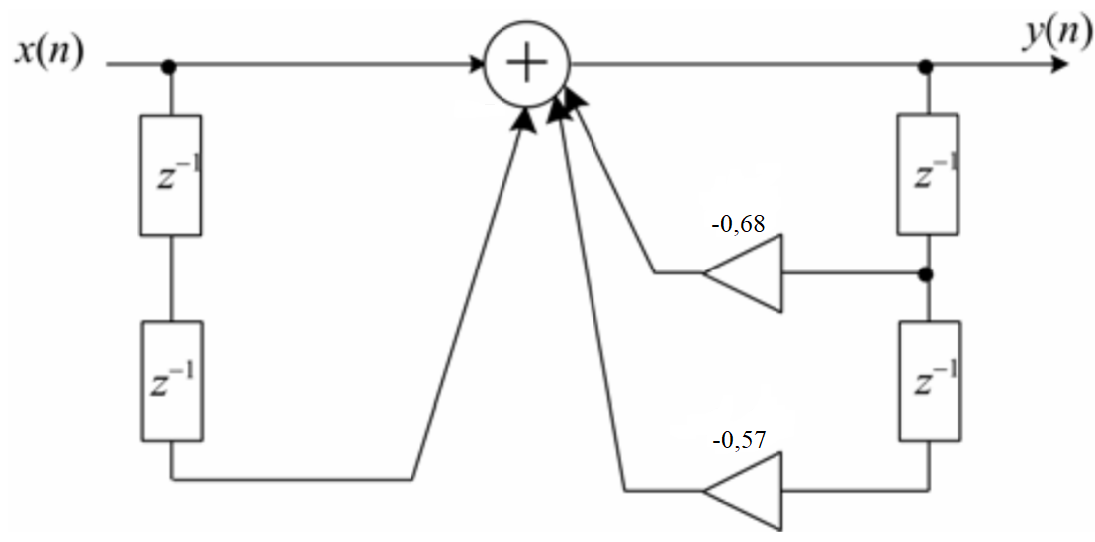 Рис. 3. 5 Структурная схема базового звена 2-го порядка 4. Используя методику п. 1.4.4, на основе общей формулы импульсной характеристики небазового звена с учетом нулевых начальных условий (1.56) запишем 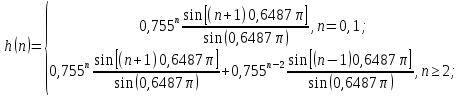 (3.3) (3.3)где значения r* и φ* рассчитаны по формулам (1.54) и (1.53) и равны: 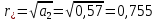 ; ;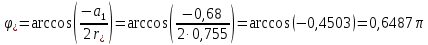 5. Результаты расчета 5 точек ИХ по формуле (3.3) с точностью до 4-го знака после запятой приведены в табл. 3.1. Таблица 3.1 Вычисление их по формуле (3.3)
6. Расчет ИХ по РУ выполняется методом прямой подстановки (см. п.1.3.4) при нулевых начальных условиях. Выполнив в РУ (3.2а) подстановку (1.21), запишем уравнение h(n) = u0(n) + u0(n − 2) − 0,68 h(n −1) − 0,57·h(n − 2) (3.4а) результаты решения которого с точностью до 4-го знака после запятой приведены в табл. 3.2а. Таблица 3.2а Вычисление ИХ по РУ (3.4а)
7. Результаты вычислений ИХ двумя способами в пп. 5, 6 совпадают. 8. График ИХ (5 отсчетов) представлен на рис. 3.6. 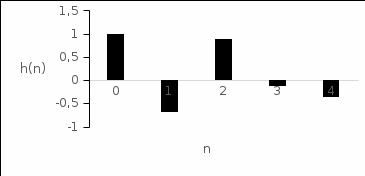 Рис. 3.6. Импульсная характеристика (к примеру 3.2) 9. Для построения карты нулей и полюсов необходимо вычислить нули и полюсы ПФ (3.1) по методике, приведенной в п. 1.4.6. Комплексно-сопряженные полюсы в показательной форме 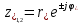 с учетом рассчитанных в п. 4 значений r* и ϕ* равны 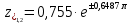 Т.к. коэффициент b0=1, то вычисление комплексно-сопряженных нулей можно упростить 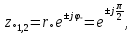 Где 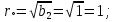  Карта нулей и полюсов изображена на рис. 3.11а; 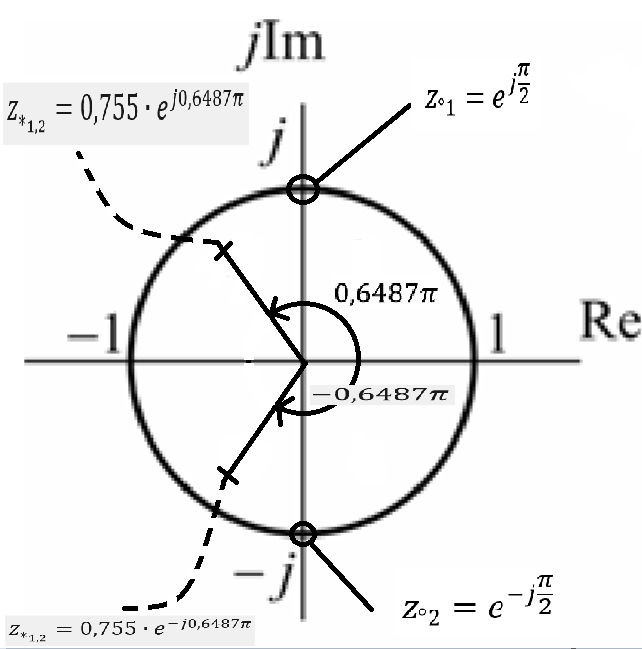 Рис. 3. 11а Карта нулей и полюсов (к примеру 3.1а) 10. Для расчета значений АЧХ и ФЧХ звена 2-го порядка в произвольной точке необходимо использовать общие формулы (1.81)–(1.82): 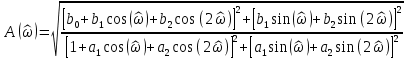 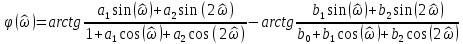 подставляя в них заданные значения коэффициентов. 11. В данном случае карта нулей и полюсов содержит два комплексно-сопряженных полюса и два нуля, лежащих на единичной окружности на границах основной полосы частот, поэтому относительно АЧХ можно сделать следующие выводы. В основной полосе частот  ∈[0; π] АЧХ звена 2-го порядка (3.5а) является непрерывной функцией, при этом: ∈[0; π] АЧХ звена 2-го порядка (3.5а) является непрерывной функцией, при этом:- внутри основной полосы частот АЧХ имеет один максимум, расположенный приблизительно на частоте полюса  ; ;- внутри основной полосы частот АЧХ не имеет минимума; - на границах основной полосы частот  АЧХ равна нулю; нули АЧХ не являются ее минимумами. АЧХ равна нулю; нули АЧХ не являются ее минимумами. Относительно ФЧХ можно сказать, что она представляет собой непрерывную функцию, имеющую на границах основной полосы скачки на π. 12. В данном примере следует вычислить значения АЧХ и ФЧХ в трех точках: А) в точке 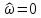 при z = 1 при z = 1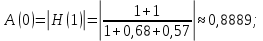 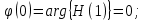 Б) в точке  при z=-1 при z=-1  В) в точке максимума АЧХ  , который находится приблизительно на частоте ϕ* полюса , который находится приблизительно на частоте ϕ* полюса Значения АЧХ и ФЧХ в этой точке равны: 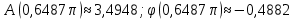 13. Графики нормированных АЧХ и ФЧХ, построенные на основе качественного анализа и экспресс-анализа, представлены на рис. 3.4.  Рис. 3. 4 Графики нормированных АЧХ и ФЧХ |