Порфиров 7. 1. Естественная область определения кривой Регулярность

• Название: 1. Естественная область определения кривой Регулярность
• Дата: 19.01.2023
• Размер: 160.06 Kb.
• Имя файла: Порфиров 7.docx
• Тип: Документы; #894986

1. «Естественная» область определения кривой 

 

2. Регулярность:

а)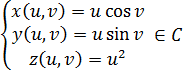 

 

б) Проверим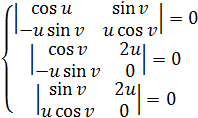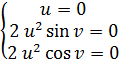 

 

 – особая точка

точка   - особая точка

 поверхность с особой точкой.

 

 3. Запишем уравнения координатных линий и выясним, что это за кривые:

u – линия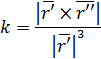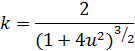 

   семейство парабол

















 – семейство плоских кривых

v – линия u 

 семейство окружностей,   лежащих в плоскости 

4. Составим уравнение касательной плоскости и нормали в произвольной точке.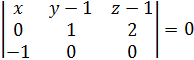

 









 – касательная плоскость



 

5. Найдем первую квадратичную форму:











 

6. Найти угол между координатными линиями

 координатная сеть ортогональна.

 

7. Найдем или оценим площадь части поверхности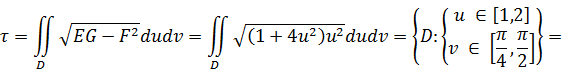







 

8. Найдем вторую квадратичную форму

























9. Составим уравнение индикатрисы Дюпена и определим геометрическое место точек.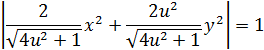



 (область регулярности поверхности)



 

10. Найдем главную кривизну поверхности, гауссову и среднюю кривизну: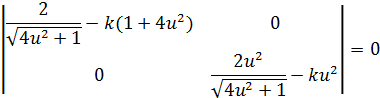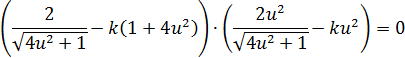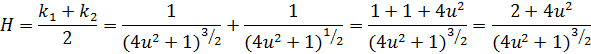















 

11. Определим тип точек поверхности.

Так как   эллиптические точки

 

12. Выясним изометрична ли поверхность:

а) плоскость 



б) сфера 



в) псевдосфера 




13. Является ли поверхность минимальной?

Так как   , то поверхность не минимальна.

14. Запишем уравнение геодезических кривых на поверхности и определим их геометрические образы:

Символ Кристофеля: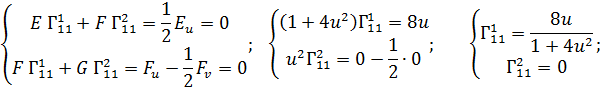















Так как параболоид поверхность вращения, то геодезическими линиями являются меридианы: в данном случае u- линии, v=const:   .