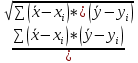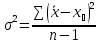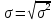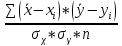Хурда Анастасия Викторовна
Группа JO-Б16А-03 (33)
Задание №27
Рассчитать корреляционную зависимость между длиной тела (см) и результатом бега на 100 метров (сек).
№ п/п
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
X (см)
|
177
|
180
|
183
|
164
|
176
|
182
|
177
|
175
|
171
|
180
|
185
|
177
|
182
|
182
|
Y (сек)
|
11,8
|
12,3
|
12,6
|
12,3
|
13,0
|
12,5
|
12,0
|
11,9
|
12,8
|
12,4
|
12,4
|
12,2
|
12,8
|
12,8
|
Рассчитаем 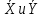
Рассчитаем разность (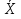 -Xi) и ( -Xi) и (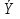 -Yi) -Yi)
Введем в квадрат 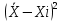 и и 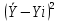
Рассчитаем произведения этих разностей 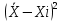 * * 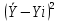
Рассчитаем сумму квадратов разностей для каждого показателя ∑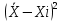 , ∑ , ∑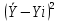
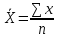 ; ; 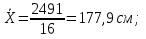 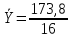 =12,4 сек =12,4 сек
Занесем данные в таблицу с учетом того, что 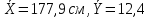 сек сек
n
|
X
|
Y
|
(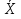 -Xi) -Xi)
|
(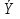 -Yi) -Yi)
|
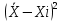
|
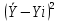
|
(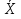 -Xi)* ( -Xi)* (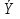 -Yi) -Yi)
|
1
|
177
|
11,8
|
1
|
0,614
|
0,86
|
0,37
|
0,5704
|
2
|
180
|
12,3
|
-2
|
0,114
|
4,29
|
0,01
|
-0,2367
|
3
|
183
|
12,6
|
-5
|
-0,185
|
25,71
|
0,03
|
0,9418
|
4
|
164
|
12,3
|
14
|
0,114
|
194
|
0,01
|
1,5918
|
5
|
176
|
13
|
2
|
-0,585
|
3,71
|
0,34
|
-1,1295
|
6
|
182
|
12,5
|
-4
|
-0,085
|
16,57
|
0,007
|
0,3489
|
7
|
177
|
12
|
1
|
0,414
|
0,86
|
0,171
|
0,3846
|
8
|
175
|
11,9
|
3
|
0,514
|
8,57
|
0,264
|
1,5061
|
9
|
171
|
12,8
|
7
|
-0,385
|
48
|
0,148
|
-2,6724
|
10
|
180
|
12,4
|
-2
|
0,014
|
4,29
|
0,0002
|
-0,0295
|
11
|
185
|
12,4
|
-7
|
0,014
|
50
|
0,0002
|
-0,1010
|
12
|
177
|
12,2
|
1
|
0,214
|
0,86
|
0,045
|
0,1989
|
13
|
182
|
12,8
|
-4
|
-0,385
|
16,5
|
0,148
|
1,5704
|
14
|
182
|
12,8
|
-4
|
-0,385
|
16,5
|
0,148
|
1,5704
|
Суммируем каждый из трех последних столбцов
∑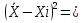 390,9 390,9 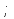 ∑ ∑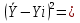 1,7 ; ∑ 1,7 ; ∑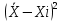 * * 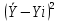 = 4,5 = 4,5
Рассчитаем коэффициент корреляции по формуле: r =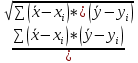
r =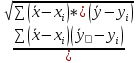 = = 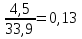
Рассчитаем Дисперсию по формуле: 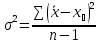
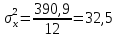 см ; см ; 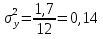 сек сек
Рассчитаем среднее квадратичное отклонение по формуле: 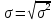
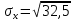 = 5,7 см ; = 5,7 см ; 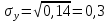 сек сек
Рассчитаем коэффициент корреляции по формуле: r = 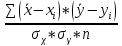
r = 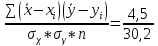 = 0,14 = 0,14
Вывод: т.к r = 0,1, можно утверждать, что корреляционная взаимосвязь присутствует, она положительная и слабая по силе. Это значит, что, чем больше длина тела, тем результат бега на 100м будет лучше, но эта взаимосвязь выражена очень слабо. |
 Скачать 19.64 Kb.
Скачать 19.64 Kb.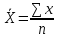 ;
; 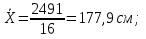
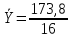 =12,4 сек
=12,4 сек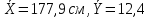 сек
сек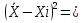 390,9
390,9 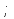 ∑
∑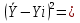 1,7 ; ∑
1,7 ; ∑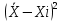 *
* 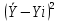 = 4,5
= 4,5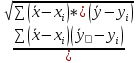 =
= 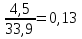
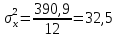 см ;
см ; 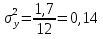 сек
сек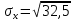 = 5,7 см ;
= 5,7 см ; 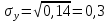 сек
сек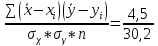 = 0,14
= 0,14
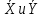
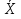 -Xi) и (
-Xi) и (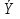 -Yi)
-Yi)