|
|
№4 күрделі және кері функция. И. бдікрімов атындаы ызылорда аграрлы техникалы жоары колледжі
И. Әбдікәрімов атындағы Қызылорда аграрлық техникалық жоғары колледжі
Бекітемін:
ПӘК төрайымы _______________
Педагогтің аты-жөні:
|
Дүйсебаева Жұлдызай
|
Бөлімі:
|
Функция
|
Күні:
|
|
Тобы:
Пәні: математика
|
ПГС-22о, ПСК-22о, АГ-22о, З-22о
Қатысушылар саны: Қатыспағандар саны:
|
Сабақтың тақырыбы:
|
Күрделі функциялар. Өзара кері функциялар
|
Оқу бағдарламасына сәйкес оқу мақсаты
|
10.3.1.6 - f(g(x)) күрделі функциясын ажырата білу және функциялар композициясын құру
|
Сабақтың мақсаты
|
Күрделі функцияны құра білу немесе күрделі функцияны элементар функцияларға жіктей білу дағдыларын қалыптастыру , берілген функцияға кері функция таба алады, функцияның периодын таба алады, монотонды аралығын анықтай алады
|
Сабақ барысы
Сабақ кезеңі/
Уақыты
|
Педагогтің іс-әрекеті
|
Оқушының іс-әрекеті
|
Бағалау
|
Ресурстар
|
Сабақтың басы
|
I .Ұйымдaстыруы бөлiмi: Оқушылaрмен aмaндaсып, оқушы нaзaрын шоғырлaндыру.
II. Ширaту жaттығуы: «Миғa шaбуыл» әдiсi aрқылы өткен сaбaқ тaқырыбынa бaйлaнысты оқушылaрдың қызығушылығын туғызу,бiлiмдерiн тексерiп,белсендi болуға шақыру.
y = f(x) + a функциясының графигінy = f(x)функциясының графигін Уосібойынша :а бірлік жоғары, егерa >0 а бірлік төмен, егер a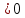 жылжыту арқылы алуға болады (ақиқат) жылжыту арқылы алуға болады (ақиқат)
y = f(x-а) функциясының графигін y = f(x) функциясының графигін Х осі бойынша : а бірлік оңға, егер a>0
а бірлік солға, егер a<0 жылжыту арқылы алуға болады (жалған)
y = f(2x) функциясының графигін, y = f(x) функциясының графигін Х осі бойынша 2 есе сығу арқылы аламыз (ақиқат)
|
Кім жылдам?.
1.Функцияның анықталу облысы, мәндер жиыны
2.Функцияның нөлдері
3. Функцияның ең кіші оң периодын табу
4. Функцияның таңба тұрақтылық аралықтары
5. Функцияның өспелі, кемімелі аралықтары
6.Функцияның экстремумдары
7.Функцияның тақтығы, жұптығы
|
Мұғалім берген тапсырмасын орындау арқылы студенттердің сабаққа дайындықтарын тексеру
|
Оқулық 10 сынып алгебра және анализ бастамалары.
|
|
Жаңа сабақ
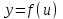 функциясын қарастырайық. Аргументі басқа бір функция болатын жаңа функциясын қарастырайық. Аргументі басқа бір функция болатын жаңа 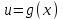 функциясын құрастырайық. функциясын құрастырайық.
Мысалы: 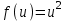 , , 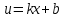 ; ; 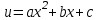 ; ; 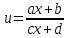 болсын. Аргументі болсын. Аргументі 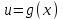 болатын болатын 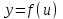 функциясынан алынған функцияның түр: функциясынан алынған функцияның түр: 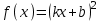 ; ; 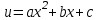 ; ; 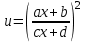
Анықтама: 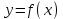 функциясынының х аргументінің орнына функциясынының х аргументінің орнына 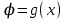 функциясы алынған функциясы алынған 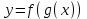 түріндегі функциясы күрделі функция деп аталады. түріндегі функциясы күрделі функция деп аталады.
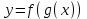 күрделі функциясы күрделі функциясы 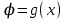 функциясының мәндері функциясының мәндері 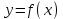 функциясының анықталу облысына кіретін х тәуелсіз айнымалысы үшін анықталған. функциясының анықталу облысына кіретін х тәуелсіз айнымалысы үшін анықталған.
№1 мысал: Егер 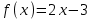 және және 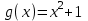 болса, f(g(x)) пен g(f(x))-ті табыңыз. болса, f(g(x)) пен g(f(x))-ті табыңыз.
Шешуі:
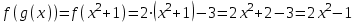
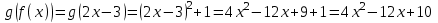
№2 мысал:
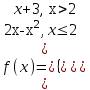 және және 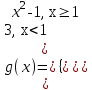 берілген. берілген. 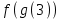 - ті табыңыз. - ті табыңыз.
Шешуі: 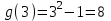 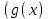 -тің 1-ші бөлігін пайдаланамыз, өйткені -тің 1-ші бөлігін пайдаланамыз, өйткені 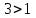 ) )
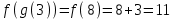 (8>2) (8>2)
Тапсырмалар:
№1. Егер 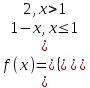 және және 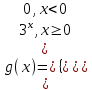 болса, болса, 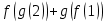 неге тең? неге тең?
№2. Егер 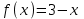 және және 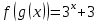 болса, болса, 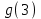 -ті табыңыз. -ті табыңыз.
|
Мысалы, функциялар берілген:
А ) у = х2;
B) у = (х+1)2;
C) y = (2х+1)2;
D) y= (2х)2;
E) y= х)2;
F)
1. Берілген функциялардың формулаларын салыстырыңыздар.
2. Бұл формуалардың ұқсастығы мен айырмашылықтарын жұптасып талқылаңыздар.
Өздік жұмысы:
f(x) = 3х-1, g(x)=2x-1 функциялары берілген. оларды
|
|
|
Сабақтың соңы
|
Рефлексия
Жұпқа бөлініңіздер.
3 ұйғарым жазыңыз, оның біреуі жалған болып табылады.
Өз ұйғарымыңызды басқа жұпқа беріңіздер.
Екінші жұп ұйғарымды оқиды және
үш жауаптың кайсысы дұрыс еместігін талқылайды
|
|
|
|
|
|
|
 Скачать 59.65 Kb.
Скачать 59.65 Kb.