Отчет. КОЙНИЕВ. I. Исторические и психологопедагогические основы исследуемой темы
 Скачать 323.5 Kb.
|
Ч1 + Ч2 = ЦТ   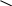 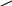   еперь разберем дом. Можно снять крышу и останется стена, а можно убрать стену и останется крыша. Если от целого отнять часть, то получится другая его часть Ц – Ч 1 = Ч 2. Зная это, ребенок может теперь сам определить неизвестную часть, имея целое и известную часть. Это уже уравнение. В нем появляется мистер Икс. – х = Ч 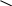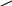то же случилось с карандашом? Что спрятал мистер Икс? Ну, конечно, у него сломался грифель. х = . Когда работают с уравнением, то пишут три строчки. В каждой из них обязательно есть х и один знак равенства. Строчка 1 – уравнение; в нем х спрятался. Строчка 2 – решение уравнения; х в одной стороне равенства, а остальное – в другой. Строчка 3 – корень уравнения; в нем открывается всем, что спрятал х. Решим такое уравнение: - х = Что же осталось, если у моркови отрезали зеленый хвостик? Решение: х = - х = Здесь два места, в которых х слева от знака равенства в одиночестве. Нижняя часть явно показывает, что корень моркови это и есть корень уравнения. Верхняя- Подробно рассказывает, как мы действуем, чтобы найти корень, то есть решаем уравнение: показываем, как из целого (моркови) и известной части (хвостика) узнаем неизвестную часть ( корень). Ц – Ч изв.= Ч н  А теперь нарисуем ракету. У нее отпадает ступень с горючим и остается ракетоноситель.    - х = Показывают как от ракеты отпадает ступень с горючим. Рисуют отпавшую часть – корень уравнения. Затем дети сочиняют свои уравнения по схемам. Например: Ц - х = Ч изв. х = Ц – Ч изв. Х = Ч (та, которая спряталась в первой строчке.) Теперь решим уравнение, где х перебрался на другое место. + х = Ч изв. + х = Ц Р |