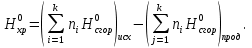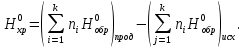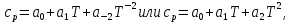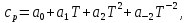Шаблон 2018-1. И. О. Фамилия Термодинамическое исследование химического процесса
 Скачать 91.2 Kb. Скачать 91.2 Kb.
|
СодержаниеВведение 4 1. Теоретическая часть 5 1.1. Общие теоретические представления о термодинамическом анализе 5 1.2. Получение метана 13 2 Основная часть Определение возможности, направления и предела протекания исследуемого химического процесса 14 2.2. Вывод зависимости изменения энтальпии от температуры 16 2.3. Нахождение зависимости изменения энтропии от температуры 18 2.4. Зависимость изменения энергии Гиббса от температуры 20 Заключение 22 Список использованных источников 23 ВведениеВ курсовой работе предложен термодинамический расчет предположительного объекта автоматизации – химического процесса гидрирования метилового спирта с целью предварительного определения возможности, направления и предела протекания процесса. На текущем этапе расчета необходимо определить изменение энтальпии, энтропии, температурного коэффициента теплового эффекта реакции, энергии Гиббса и логарифма константы равновесия в зависимости от температуры. Расчет перечисленных термодинамических характеристик производился на основе справочных данных. Основная цель термодинамических исследований – теоретическое обоснование возможности практической реализации выбранного способа производства, а также получение данных по предельной эффективности данного химического процесса. 1. Теоретическая часть1.1. Общие теоретические представления о термодинамическом анализеХимическая термодинамика изучает применение законов термодинамики к химическим, физико-химическим явлениям, связанным с разработкой новых технологических процессов. Главными задачами, которые решаются химической термодинамикой, являются: 1. Расчет физико-химических и термодинамических величин исходных и конечных веществ, получающихся в процессе. 2. Определение технологически приемлемых условий, при которых данный процесс становится термодинамически возможным. 3. Выбор оптимальных условий проведения процесса. 4. Расчет материального и теплового баланса разрабатываемой технологии. Тепловые балансы составляются на основе первого начала термодинамики. Анализ фазового и химического равновесия осуществляется на основе второго начала термодинамики. В качестве объекта автоматизации может быть любая термодинамическая система. Термодинамическая система – это конкретный материальный объект, выделенный из окружающей среды с реально существующими и воображаемыми поверхностями раздела. Системой может быть, например, любая химическая реакция, протекающая как в реакторе, так и в лабораторной колбе. Система является гомогенной, если она однородна во всех точках. Если она имеет поверхность раздела, то в этом случае говорят о гетерогенной системе, состоящей из нескольких фаз. Фаза – это совокупность однородных материальных частей системы, отделенных друг от друга поверхностями раздела. В зависимости от взаимодействия с окружающей средой системы могут быть: изолированными, не обменивающимися с внешним миром ни энергией, ни веществом; закрытыми (или замкнутыми) – обменивающимися только энергией и открытыми – обменивающимися и энергией и веществом. Совокупность всех физических и химических свойств системы характеризует ее состояние. Отдельная величина, определяющая состояние системы, является термодинамическим параметром состояния. Всякое изменение, происходящее в системе и связанное с изменением хотя бы одного из термодинамических параметров состояния, называется термодинамическим процессом. Процессы, которые осуществляются при постоянном давлении, называются изобарными; при постоянной температуре – изотермическими, а при постоянном объеме – изохорными. Процессы, при которых система не обменивается с окружающей средой теплотой, называются – адиабатными. Термодинамический процесс является обратимым, если допускается возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. В противном случае процесс является необратимым. Общая мера материального движения, при его превращении из одного вида в другой, называется энергией. Различают различные формы движения, в связи с чем вводятся соответствующие им виды энергии: механическая, внутренняя, химическая. Полная энергия системы включает внешнюю и внутреннюю энергии. При взаимодействии системы с окружающей средой возможны два качественно различных способа передачи энергии – в форме работы и в форме теплоты. Работа, таким образом, является мерой энергии. Она представляет собой одну из форм передачи энергии от системы к системе. Теплота – это энергия, передаваемая одним телом другому при их взаимодействии, зависящая лишь от температуры этих тел и не связанная с переносом вещества от одного тела к другому. Теплоту, подводимую к системе, в термодинамике принято считать положительной, а отданную ей – отрицательной. Аналитическое выражение первого начала связывает изменение внутренней энергии изолированной системы 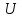 , теплоту , теплоту 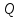 и работу и работу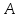 : :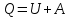 . .Многие термодинамические расчеты в физической химии базируются на законе Гесса и его следствиях. По закону Гесса тепловой эффект химической реакции 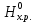 не зависит от пути протекания процесса. не зависит от пути протекания процесса.Если известны стандартные теплоты (энтальпии) сгорания участников реакции 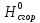 , то по следствию из закона Гесса стандартный тепловой эффект , то по следствию из закона Гесса стандартный тепловой эффект
Если известны стандартные теплоты (энтальпии) образования участников реакции 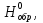 то по следствию из закона Гесса стандартный тепловой эффект то по следствию из закона Гесса стандартный тепловой эффект
В уравнениях (1) и (2) индексы относятся к исходным веществам и продуктам реакции, их число 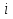 и и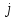 может изменяться от 1 до может изменяться от 1 до 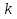 и и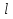 . Так, для реакции . Так, для реакции 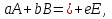 в которой вещества А и В – реагенты, L и E – продукты, тепловой эффект можно рассчитать как 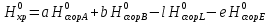 или 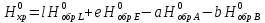 . .В справочниках можно найти теплоты (энтальпии) образования и сгорания веществ, находящихся в стандартном состоянии . При температурах, не равных 298 К, для расчета тепловых эффектов используют уравнение Кирхгофа: 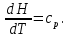 Интегрирование уравнения Кирхгофа (определенное и неопределенное) можно проводить при разных условиях. Например, если 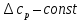 , то тепловой эффект реакции можно рассчитать по формуле , то тепловой эффект реакции можно рассчитать по формуле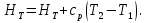 Для условия 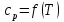 нужно учитывать влияние температуры на теплоемкость нужно учитывать влияние температуры на теплоемкость 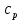 веществ − участников реакции, которое отражают эмпирические уравнения: веществ − участников реакции, которое отражают эмпирические уравнения:
где 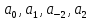 – температурные коэффициенты. Коэффициент – температурные коэффициенты. Коэффициент 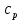 в уравнении Кирхгофа определяется как в уравнении Кирхгофа определяется как
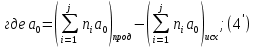 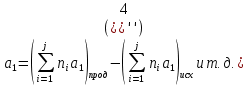 Обычно коэффициент 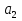 используется для органических, коэффициент используется для органических, коэффициент 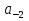 – для неорганических веществ, поэтому в уравнении (4) может отсутствовать третье или четвертое слагаемое. Для реакций с участием органических и неорганических веществ в уравнении (4), как правило, присутствуют четыре слагаемых. – для неорганических веществ, поэтому в уравнении (4) может отсутствовать третье или четвертое слагаемое. Для реакций с участием органических и неорганических веществ в уравнении (4), как правило, присутствуют четыре слагаемых.В диапазоне температур от стандартной (298 К) до 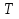 уравнение Кирхгофа имеет вид уравнение Кирхгофа имеет вид 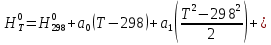 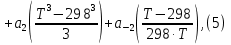 где 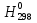 – стандартный тепловой эффект химической реакции, который рассчитывается по уравнению (2) при стандартной температуре. – стандартный тепловой эффект химической реакции, который рассчитывается по уравнению (2) при стандартной температуре. Уравнения (1, 2 и 5) используются для расчета изобарного теплового эффекта ( 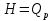 ); изохорный ( ); изохорный (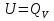 ) можно рассчитать из соотношения ) можно рассчитать из соотношения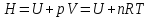 . .Таким образом, связь изобарного и изохорного тепловых эффектов определяет соотношение 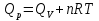 , ,в котором 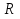 – универсальная газовая константа; – универсальная газовая константа; 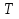 – температура; – температура;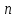 – изменение числа молей газообразных веществ в реакции – изменение числа молей газообразных веществ в реакции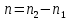 , ,где 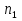 – суммарное число молей газообразных веществ в начальном состоянии, – суммарное число молей газообразных веществ в начальном состоянии, 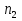 – суммарное число молей образовавшихся газообразных веществ. – суммарное число молей образовавшихся газообразных веществ.Температурная зависимость теплоемкости по уравнению (3) используется для расчета количества тепла 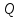 , затрачиваемого на нагревание: , затрачиваемого на нагревание: 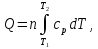 (6) (6)где 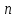 число молей вещества. число молей вещества.Второе начало термодинамики оперирует понятием энтропии 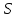 , связанной с термодинамической вероятностью состояния системы, состоящей из большого числа частиц (молекул и атомов), и устанавливает закон изменения энтропии при протекании самопроизвольных процессов. Энтропия – основная термодинамическая функция, с помощью которой можно предсказать направление естественных процессов, учитывая изменения как в системе, так и во внешней среде. , связанной с термодинамической вероятностью состояния системы, состоящей из большого числа частиц (молекул и атомов), и устанавливает закон изменения энтропии при протекании самопроизвольных процессов. Энтропия – основная термодинамическая функция, с помощью которой можно предсказать направление естественных процессов, учитывая изменения как в системе, так и во внешней среде.Аналитическое выражение второго начала термодинамики для обратимых и необратимых процессов имеет вид 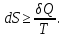 Знак равенства соответствует обратимым процессам: при обратимых процессах в изолированной системе энтропия остается постоянной. Знак неравенства соответствует необратимым процессам: при протекании необратимого процесса в изолированной системе энтропия возрастает. Неравенство 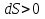 является условием самопроизвольности данного процесса в изолированной системе. является условием самопроизвольности данного процесса в изолированной системе.Если процесс обратим, то в изолированной системе он будет протекать в том направлении, которое сопровождается увеличением энтропии. При самопроизвольном протекании процесса в изолированной системе энтропия увеличивается и одновременно система приближается к состоянию равновесия. Когда система достигнет состояния равновесия, все процессы прекратятся и энтропия будет максимальной, то есть равновесное состояние изолированной системы – это состояние с максимальной энтропией. Таким образом, в изолированных системах энтропия является критерием возможности и направления процесса, а так же состояния термодинамического равновесия. Ее изменение в химических процессах можно рассчитать по уравнению 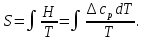 В диапазоне от 298 К до 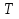 изменение энтропии составит изменение энтропии составит 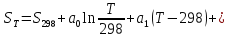 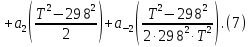 В открытых системах в качестве критериев направления процесса и равновесия в системе используют свободную энергию Гиббса 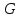 и свободную энергию Гельмгольца и свободную энергию Гельмгольца 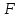 : :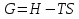 и и 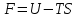 . .Эти величины, в отличие от энтропии, относятся только к системе, их использование упрощает анализ изменений в системе и лежит в основе аппарата прикладной химической термодинамики. Если при постоянной температуре меняется состояние исследуемой системы, соответствующие изменения свободных энергий Гиббса 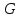 и Гельмгольца и Гельмгольца 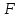 составят составят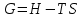 и и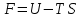 . .Свободная энергия Гиббса системы в изобарно-изотермических условиях уменьшается при необратимых процессах и остается постоянной при обратимых процессах (критерий самопроизвольного протекания процесса): 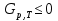 . .Равновесное состояние системы соответствует минимуму свободной энергии Гиббса, поэтому условие равновесия имеет вид 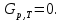 Свободная энергия Гельмгольца системы в изохорно-изотермических условиях уменьшается при необратимых процессах и остается постоянной при обратимых процессах (критерий самопроизвольного протекания процесса): 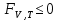 . .Равновесное состояние системы соответствует минимуму свободной энергии Гельмгольца, поэтому условие равновесия выражается равенством 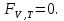 Стоит заметить, что приведенные выше соотношения даны для конечных изменений величин в системе, которые выражены через символ Δ. В теоретических основах физической химии чаще рассматриваются бесконечно малые изменения этих величин и используется символ дифференциала 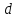 . Для бесконечно малых изменений в системе объединенное выражение первого и второго начала термодинамики имеет вид . Для бесконечно малых изменений в системе объединенное выражение первого и второго начала термодинамики имеет вид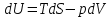 . (8) . (8)Уравнение (8) применимо к любым процессам (обратимым и необратимым), происходящим в закрытой системе при наличии единственного вида работы – работы расширения. Согласно уравнению (8) внутренняя энергия закрытой системы меняется при изменении энтропии и объема: 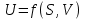 . .Полный дифференциал функции составит 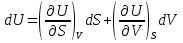 . .При сравнении полученного уравнения с уравнением (7) обнаруживаются соотношения 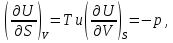 которые связаны с понятием характеристических функций – таких функций, с помощью которых или их производных можно выражать свойства систем, то есть давление и температура – характеристические функции. Для свободной энергии Гиббса можно получить соотношения: 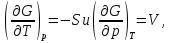 где объем и энтропия – характеристические функции. Тогда c помощью характеристических функций можно получить парное соотношение, которое называется уравнением Гиббса – Гельмгольца: где объем и энтропия – характеристические функции. Тогда c помощью характеристических функций можно получить парное соотношение, которое называется уравнением Гиббса – Гельмгольца: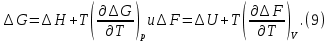 В большинстве случаев величины 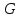 и и 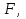 тем более тем более 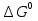 и и 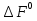 могут быть легко определены. С учетом уравнений (5) и (6) расчетная формула для стандартной энергии Гиббса имеет вид могут быть легко определены. С учетом уравнений (5) и (6) расчетная формула для стандартной энергии Гиббса имеет вид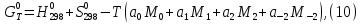 где 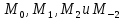 – независимые от температуры коэффициенты. – независимые от температуры коэффициенты.Приведенное уравнение называется уравнением Темкина – Шварцмана, оно часто используется для упрощения расчетов. Не менее важным для термодинамического анализа является применение учения о химическом равновесии. Учение о химическом равновесии рассматривает вопросы, связанные с расчетом химического равновесия, устойчивости системы, направленности процесса, а также определением оптимальных условий режима химического процесса и т. п. Если реакция 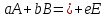 протекает в смеси идеальных газов 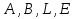 с начальными (неравновесными) парциальными давлениями с начальными (неравновесными) парциальными давлениями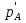 , ,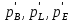 , то при достижении равновесия в ней участники реакции характеризуются равновесными давлениями , то при достижении равновесия в ней участники реакции характеризуются равновесными давлениями 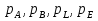 и уравнение изотермы химической реакции Вант-Гоффа имеет вид и уравнение изотермы химической реакции Вант-Гоффа имеет вид 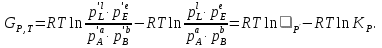 Величина и знак свободной энергии Гиббса зависят от соотношения величин 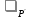 и и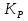 . При . При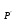 < <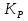 самопроизвольный процесс пойдет слева направо ( самопроизвольный процесс пойдет слева направо (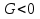 ); при ); при 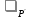 = =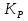 реакция достигает равновесного состояния ( реакция достигает равновесного состояния (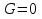 ) и при ) и при 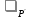 > >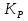 процесс, возможно, пойдет в обратном направлении ( процесс, возможно, пойдет в обратном направлении (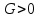 ). ).Если рассматриваемая реакция находится в стандартном состоянии ( 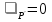 ), то ее характеризует изменение стандартной свободной энергии Гиббса ), то ее характеризует изменение стандартной свободной энергии Гиббса 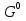 и стандартная константа равновесия и стандартная константа равновесия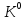 . Стандартная константа равновесия связана с константой равновесия . Стандартная константа равновесия связана с константой равновесия 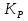 соотношением соотношением 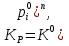 где 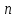 – приращение числа молей при протекании реакции, например, для рассматриваемой реакции – приращение числа молей при протекании реакции, например, для рассматриваемой реакции 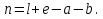 Изменение свободной энергии Гиббса равно разности ее значений для конечных и начальных веществ: 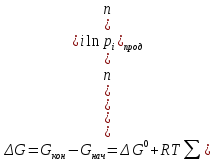 , ,где 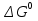 − стандартное изменение свободной энергии Гиббса − стандартное изменение свободной энергии Гиббса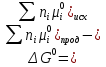 . .При каждой температуре эта величина остается постоянной для данной реакции, так как в этих условиях постоянны химические потенциалы участников реакции. В условиях равновесия при 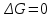 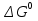 и и 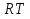 постоянны, следовательно, должна быть постоянной и разность постоянны, следовательно, должна быть постоянной и разность 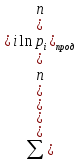 . Эту разность обозначим как . Эту разность обозначим как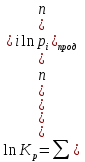 . .Таким образом, для рассматриваемой реакции 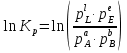 и и 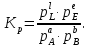 Соотношение для константы равновесия 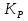 применимо и тогда, когда концентрации компонентов выражены через молярные доли или молярную концентрацию: применимо и тогда, когда концентрации компонентов выражены через молярные доли или молярную концентрацию: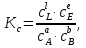 а также для реакций в смеси реальных газов и в неидеальных растворах. В последних случаях используются фугитивности и активности участников реакции, например, для активностей участников реакции выражение для константы равновесия имеет вид 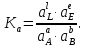 |