Шаблон 2018-1. И. О. Фамилия Термодинамическое исследование химического процесса
 Скачать 91.2 Kb. Скачать 91.2 Kb.
|
2.2. Вывод зависимости изменения энтальпии от температурыРассчитаем зависимость изменения энтальпии от температуры. ΔH0Т = f(T) ΔH0Т = ΔH0298 + 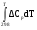  ΔCp = а0 + Δа1·103 T + Δа2·106 T2 + Δа-2·10-5 T-2 ΔH0Т = –115650 +  (а0 + Δа1·10-3 T + Δа2·10-6 T2 + Δа-2·105 T-2 ) dT (а0 + Δа1·10-3 T + Δа2·10-6 T2 + Δа-2·105 T-2 ) dTΔH0Т = –115650 +  (61,76 –23,09·10-3 T + 13,61·10-6 T2 – 0,22·105 T-2) dT (61,76 –23,09·10-3 T + 13,61·10-6 T2 – 0,22·105 T-2) dTΔH0Т = –115650 + 61,76 (Т –298) –23,09·10-3 ((Т2 –2982)/2) + 13,61·10-6 ((Т3 –2983)/3) + 0,22·105 ((1/Т) – (1/298)) ΔH0Т = –115650 + 61,76 Т –18404,5 –11,55·10-3 Т2 +1025,7 + 4,54·10-6 Т3 –120,1 + 0,22·105 (1/Т) – 73,8 Приводим подобные: ΔH0Т = –133222,7 + 61,76 Т – 11,55·10-3 Т2 + 4,54·10-6 Т3 + 0,22·105 (1/Т) (Уравнение зависимости изменения энтальпии от температуры) Проверка уравнения ΔH0Т = f(T): ΔH0298 = –133222,7 + 61,76 ·298 – 11,55·10-3 ·2982 + 4,54·10-6 ·2983+ 0,22·105 (1/298) = –133222,7 + 18404,5 – 1025,7 + 120,1+ 73,8 = –115650 Дж/моль Данные для построения графика ΔH0Т = f(T): ΔH0400 = –133222,7 + 61,76 ·400 – 11,55·10-3 ·4002 + 4,54·10-6 ·4003+ 0,22·105 (1/400) = –110120 Дж/моль ΔH0500 = –133222,7 + 61,76 ·500 – 11,55·10-3 ·5002 + 4,54·10-6 ·5003+ 0,22·105 (1/500) = –105230 Дж/моль ΔH0600 = –133222,7 + 61,76 ·600 – 11,55·10-3 ·6002 + 4,54·10-6 ·6003+ 0,22·105 (1/600) = –101360 Дж/моль ΔH0700 = –133222,7 + 61,76 ·700 – 11,55·10-3 ·7002 + 4,54·10-6 ·7003+ 0,22·105 (1/700) = – 95360 Дж/моль ΔH0800 = –133222,7 + 61,76 ·800 – 11,55·10-3 ·8002 + 4,54·10-6 ·8003+ 0,22·105 (1/800) = – 89230 Дж/моль ΔH0900 = –133222,7 + 61,76 ·900 – 11,55·10-3 ·9002 + 4,54·10-6 ·9003+ 0,22·105 (1/900) = – 82530 Дж/моль ΔH01000 = –133222,7 + 61,76 ·1000 – 11,55·10-3 ·10002 + 4,54·10-6 ·10003+ 0,22·105 (1/1000) = –75000 Дж/моль Таблица 2.2 – Изменение энтальпии от температуры
Т, К ΔН, кДж/моль Рисунок 2.1 – Зависимость изменения энтальпии от температуры 2.3. Нахождение зависимости изменения энтропии от температурыРассчитаем зависимость изменения энтропии от температуры. ΔS0Т = f(T) ΔS0Т = ΔS0298 + 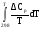  ΔCp = а0 + Δа1·103 T + Δа2·106 T2 + Δа-2·10-5 T-2 ΔS0Т = 4,71 + 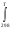 ((а0 + Δа1·10-3 T + Δа2·10-6 T2 + Δа-2·105 T-2 )/Т) dT ((а0 + Δа1·10-3 T + Δа2·10-6 T2 + Δа-2·105 T-2 )/Т) dTΔS0Т = 4,71 + 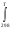 ((61,76 –23,09·10-3 T + 13,61·10-6 T2 – 0,22·105 T-2)/Т) dT ((61,76 –23,09·10-3 T + 13,61·10-6 T2 – 0,22·105 T-2)/Т) dTΔS0Т =4,71 + 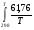 dT – dT –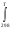 23,09·10-3 dT + 23,09·10-3 dT + 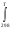 13,61·10-6 T dT – 13,61·10-6 T dT –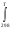 0,22·105 T-3dT 0,22·105 T-3dT ΔS0Т =4,71 + 61,76 ln (T/298) –23,09·10-3 (Т –298) + 13,61·10-6 ((Т2 –2982)/2) – 0,22·105 (1/(2·Т2) –1/(2·2982)) ΔS0Т =4,71 + 61,76 ln T– 61,76 ln 298 –23,09·10-3 Т +23,09·10-3 298 + 13,61·10-6 (Т2/2) –13,61·10-6 (2982)/2) + 0,22·105 ·(1/(2·Т2)) – 0,22·105 ·( (1/(2·2982)) ΔS0Т = 4,71 + 61,76 ln T– 352,03 –23,09·10-3 Т + 6,88 + 13,61·10-6 (Т2/2) – 0,6 + 0,22·105 ·(1/(2·Т2)) – 0,12 Приводим подобные: ΔS0Т = – 341,16 + 61,76 ln T–23,09·10-3 Т + 13,61·10-6 (Т2/2) + 0,22·105 (1/(2·Т2)) ΔS0Т = – 341,16 + 61,76 lnT–23,09·10-3Т + 6,8·10-6Т2 + 0,11·105 (1/Т2) (Уравнение зависимости изменения энтропии от температуры) Проверка уравнения ΔS0Т = f(T): ΔS0298 = – 341,16 + 61,76 ln 298 –23,09·10-3 298 + 6,8·10-6 2982 + 0,11·105 (1/2982) = –341,16 + 352,03 – 6,88 + 0,6 + 0,12 = 4,71 Дж/моль·К Данные для построения графика ΔS0Т = f(T): ΔS0400 = – 341,16 + 61,76 ln 400 –23,09·10-3 400 + 6,8·10-6 4002 + 0,11·105 (1/4002) =19,8Дж/моль·К ΔS0500 = – 341,16 + 61,76 ln 500 –23,09·10-3 500 + 6,8·10-6 5002 + 0,11·105 (1/5002) = 29,1 Дж/моль·К ΔS0600 = – 341,16 +61,76 ln 600 –23,09·10-3600 + 6,8·10-6 6002 + 0,11·105 (1/ 6002) = 45,5 Дж/моль·К ΔS0700 = – 341,16 + 61,76 ln 700 –23,09·10-3 700 + 6,8·10-6 7002 + 0,11·105 (1/7002) = 51,3 Дж/моль·К ΔS0800 = – 341,16 + 61,76 ln 800 –23,09·10-3 800 + 6,8·10-6 8002 + 0,11·105 (1/8002) = 63,4 Дж/моль·К ΔS0900= – 341,16 + 61,76 ln 900 –23,09·10-3 900 + 6,8·10-6 9002 + 0,11·105 (1/9002) = 66,1 Дж/моль·К ΔS01000 = – 341,16 + 61,76 ln 1000 –23,09·10-3 1000 + 6,8·10-6 10002 + 0,11·105 (1/10002) = 69,2 Дж/моль·К Таблица 2.3 – Изменение энтропии от температуры
ΔS, Дж/моль·К Т, К Рисунок 2.2 – Зависимость изменения энтальпии от температуры 2.4. Зависимость изменения энергии Гиббса от температурыРассчитаем зависимость изменения энергии Гиббса от температуры по формуле: ΔG0Т = ΔH0Т –TΔS0Т. Используя уравнение зависимости ΔH0Т = f(T) и ΔS0Т = f(T) получим: ΔG0Т = –133222,7 + 61,76 Т – 11,55·10-3 Т2 + 4,54·10-6 Т3 + 0,22·105 (1/Т) –T·( – 341,16 + 61,76 ln T–23,09·10-3 Т + 6,8·10-6 Т2 + 0,11·105 (1/Т2)) ΔG0Т = –133222,7 + 61,76 Т – 11,55·10-3 Т2 + 4,54·10-6 Т3 + 0,22·105 (1/Т) + 341,16 T – 61,76 T ln T+23,09·10-3 Т2 – 6,8·10-6 Т3 – 0,11·105 (1/Т)) Приводим подобные: ΔG0Т = –133222,7 + 402,92 Т + 11,54·10-3 Т2 –2,26·10-6 Т3 + 0,11·105 (1/Т) – 61,76TlnT (Уравнение зависимости изменения энергии Гиббса от температуры) Проверка уравнения ΔG0Т = f(T): ΔG0298 = –133222,7 + 402,92·298 + 11,54·10-3 2982 –2,26·10-6 2983 + 0,11·105 (1/298) – 61,76 ·298 ln 298 ΔG0298 = –133222,7 + 119823,42 + 1024,80 – 59,81+ 36,91 – 104905,54 = –117302,92 = –117,3 кДж/моль Данные для построения графика ΔG0Т = f(T): ΔG0400 = 133222,7 + 402,92·400 + 11,54·10-3 4002 –2,26·10-6 4003 + 0,11·105 (1/400) – 61,76 ·400 ln 400 = –120125 Дж/моль ΔG0500 = 133222,7 + 402,92·500 + 11,54·10-3 5002 –2,26·10-6 5003 + 0,11·105 (1/500) – 61,76 ·500 ln 500 = –122014 Дж/моль ΔG0600 = 133222,7 + 402,92·600 + 11,54·10-3 6002 –2,26·10-6 6003 + 0,11·105 (1/600) – 61,76 ·600 ln 600 = –127899 Дж/моль ΔG0700 = 133222,7 + 402,92·700 + 11,54·10-3 7002 –2,26·10-6 7003 + 0,11·105 (1/700) – 61,76 ·700 ln 700 = –135096 Дж/моль ΔG0800 = 133222,7 + 402,92·800 + 11,54·10-3 8002 –2,26·10-6 8003 + 0,11·105 (1/800) – 61,76 ·800 ln 800 = –139905 Дж/моль ΔG0900 = 133222,7 + 402,92·900 + 11,54·10-3 9002 –2,26·10-6 9003 + 0,11·105 (1/900) – 61,76 ·900 ln 900 = –142134 Дж/моль ΔG01000 = 133222,7 + 402,92·1000 + 11,54·10-3 10002 –2,26·10-6 10003 + 0,11·105 (1/1000) – 61,76 ·1000 ln 1000 = –149567Дж/моль Таблица 2.4 – Изменение энергии Гиббса от температуры
Т, К ΔG, кДж/моль Рисунок 2.3 – Зависимость изменения энергии Гиббса от температуры ЗаключениеРассчитаны термодинамические параметры предложенного химического процесса CH3OH+H2→CH4+H2O по справочным данным. Определен температурный интервал, при котором эта реакция идет без разложения газов, нижний температурный предел для всех газов одинаковый и составляет 298К. Верхний предел наименьший у метанола, составляет 1000 К. При более высоких температурах метанол будет разлагаться. Поэтому наиболее приемлемый температурный интервал для исследуемого химического процесса – 298-1000 К. На основании полученной зависимости ΔН0Т = f(T), можно сделать вывод, что с ростом температуры энтальпия химического процесса уменьшается. Установлено, что исследуемый процесс при стандартных условиях протекает с выделением теплоты. С повышением температуры количество выделяемой теплоты снижается. Из построенной зависимости ΔS0Т = f(T) видно, что с ростом температуры энтропия системы повышается. На основании полученной зависимости ΔG0Т = f(T), можно сделать вывод, что с ростом температуры энергия Гиббса химического процесса уменьшается. Таким образом, химический процесс самопроизвольно протекает в прямом направлении. Список использованных источников
Прошу прочитайте правила, в приложении обложка и задание http://www.istu.edu/docs/education/normativ/2016/sto/sto_005.pdf По возможности нормоконтроль надо соблюдать! Т, К Т, К Т, К |
