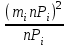Методика лабораторной работы. ОНИиПДвА (1). I. Основы методики проведения лабораторных работ Общая методика статистической обработки экспериментальных данных
 Скачать 259.74 Kb. Скачать 259.74 Kb.
|
|
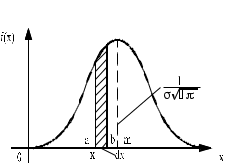
I. Основы методики проведения лабораторных работ Общая методика статистической обработки экспериментальных данных Основная особенность исследования технологических процессов, выполняемых сельскохозяйственными машинами, заключается в том, что практически все измеряемые величины носят случайный характер. Поэтому обработка результатов измерений должна быть основана на использовании основных положений теории вероятностей и математической статистики. 1. Случайные величины и их характеристика Случайной называют такую величину, которая в результате опыта может принять то или иное значение, заранее неизвестное. К случайным величинам относятся все физико-механические свойства обрабатываемого в машинах материала, значения любых технологических и энергетических показателей работы машины (глубина обработки почвы, подача хлебной массы в молотилку или зернового вороха в зерноочистительную машину, силы сопротивления обрабатываемой среды и т. п.). Различают дискретные и непрерывные случайные величины. Дискретные величины могут принимать только определенные значения, отделенные одно от другого некоторыми интервалами (например, число семян на отрезке 5 см длины рядка, число взошедших семян, число технологических отказов при работе машины и т. п.). Непрерывные случайные величины могут принимать любые значения в заданном интервале (например, размеры семян, расстояния между семенами или растениями в ряду, значения силы, необходимой для перемещения рабочего органа в обрабатываемой среде). Наиболее полной характеристикой случайной величины является закон распределения. Для дискретных случайных величин закон распределения может быть выражен в виде ряда распределения и функции распределения F(x), устанавливающей соответствие между возможными значениями х случайной величины Х и вероятностью Р их появления: 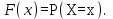 (1) (1)Непрерывную случайную величину характеризует только функция распределения, причем из-за парадокса нулевой Вероятности F(x)=P(X<x) (2) т. е. функция распределения F(x) определяет вероятность Р того события, что случайная величина X окажется меньше заранее заданного значения х. Вид функции распределения для дискретных и непрерывных случайных величин представлен на рисунке 1. 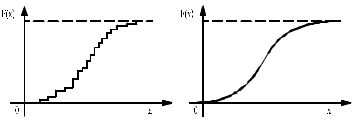 а б а–дискретных; б–непрерывных Рисунок 1 – Функция распределения случайных величин Функция распределения непрерывных случайных величин изменяется в интервале от 0 до 1: 0≤F(x)≤1 (3) Это неубывающая функция, т. е. если х2 > х1 то F(x2) > F(x1) и вероятность того, что случайная величина X попадает в интервал x1...х2, равна приращению функции на этом интервале: P(xl Функцию F(x) часто называют интегральной функцией распределения. Закон распределения непрерывных случайных величин может быть выражен также дифференциальной функцией или, что то же самое, плотностью распределения f(x) (рисунок 2): 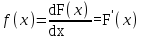 . (5) . (5)
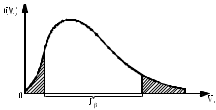
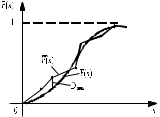
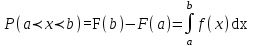 . (6) . (6)Установить вид закона распределения достаточно сложно, поэтому при обработке экспериментальных данных часто ограничиваются только числовыми характеристиками распределения случайной величины, среди которых используют математическое ожидание и дисперсию, т. е. первый начальный µ1 и второй центральный µ2 моменты: 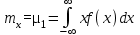 , (6) , (6)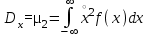 , (7) , (7)где 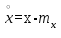 – центрированное значение случайной величины х. – центрированное значение случайной величины х.Математическое ожидание mх является мерой положения случайной величины. Это то среднее значение х, к которому она приближается, если число измерений стремится к бесконечности. Дисперсия может служить мерой рассеяния значений случайной величины относительно математического ожидания. Чем больше дисперсия, тем больше отклонения от х до mх. При использовании дисперсии в качестве меры рассеяния следует иметь в виду, что ее размерность равна квадрату размерности изучаемой величины, поэтому более удобной характеристикой рассеивания считают среднее квадратическое отклонение: 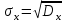 (8) (8)В качестве относительной меры рассеяния случайных величин часто используют коэффициент вариации: 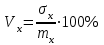 (9) (9)Характеристики рассеяния σх и Vx – основные критерии оценки качества работы некоторых сельскохозяйственных машин (сеялок, технических средств для внесения минеральных удобрении, посадочных машин). Иногда в качестве числовых характеристик используют асимметрию и эксцесс. Коэффициент асимметрии 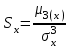 (10) (10)Эксцесс, характеризующий меру заостренности кривой f(х), 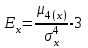 (11) (11)С помощью коэффициентов асимметрии и эксцесса изучаемые распределения можно сравнить с нормальным распределением, для которого Sx = 1, а Ех = 0. 2. Элементы математической статистики Математическая статистика – это область математики, изучающая методы сбора, обработки и анализа статистических данных с целью получения научных и практических выводов об изучаемом случайном явлении. Статистические данные представляют собой множество значений одной или нескольких случайных величин, которыми описывают соответствующие признаки данной совокупности однородных элементов, называемой генеральной совокупностью. Например, растения какой-либо культуры, выращиваемые при определенных условиях, образуют генеральную совокупность, а любой их размер (длина, диаметр) является признаком генеральной совокупности. Генеральная совокупность может содержать конечное или бесконечное число элементов. Практически невозможны и неоправданны изучение и анализ всего множества элементов генеральной совокупности. При изучении ее признаков обычно используют только одно подмножество случайно подобранных элементов или выборку. Число элементов выборки n называют объемом. Распространение результатов, полученных на основе изучения элементов выборки, на всю генеральную совокупность может привести к ошибкам, оценка которых и составляет основную задачу математической статистики. Кроме того, с помощью математической статистики проверяют гипотезы о виде закона распределения случайных величин или о равенстве однородных числовых характеристик (средних значений, дисперсий). 2.1 Точечные и интервальные оценки измеряемых величин Любое значение искомого параметра, вычисленное на основе ограниченного числа опытов, всегда содержит элемент случайности. При повторении опыта результат вычислений может оказаться другим. Такое случайное приближенное значение называют оценкой параметра. Оценкой математического ожидания может служить среднее арифметическое значение измеряемой величины в n независимых опытах. При очень большом числе опытов среднее арифметическое значение будет с большей вероятностью близким к математическому ожиданию. Если же число опытов невелико, то замена математического ожидания средним арифметическим значением приведет к некоторой ошибке, зависящей от числа опытов. Аналогично обстоит дело и с оценками других неизвестных параметров. В зависимости от предъявляемых требований различают следующие оценки параметров: – максимальное приближение к параметру (сходимость по вероятности) при увеличении числа опытов – состоятельная оценка; – отсутствие систематической ошибки в сторону завышения (занижения) – несмещенная оценка; – наименьшая дисперсия выбранной несмещенной оценки по сравнению с другими – эффективная оценка. На практике не всегда удается выбрать оценки, удовлетворяющие всем этим требованиям. Может оказаться, что если даже эффективная оценка существует, то формулы для ее вычисления оказываются слишком сложными. Иногда для простоты расчетов используют незначительно смещенные оценки. Однако выбору оценки всегда должен предшествовать ее критический анализ со всех перечисленных точек зрения. Как отмечено ранее, в качестве оценки математического ожидания обычно используют среднее арифметическое значение измерений наблюдаемой величины: 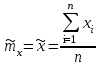 . (12) . (12)Данная оценка является состоятельной, несмещенной и эффективной. Оценка статистической дисперсии 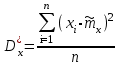 (13) (13)приводит к систематическому занижению дисперсии, т. е. является смещенной. Чтобы ликвидировать этот недостаток, достаточно ввести поправку, т. е. умножить величину Dx* на 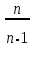 . Тогда . Тогда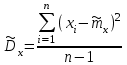 . (14) . (14)Так как при n→∞ множитель стремится к единице, то при больших значениях n погрешность оценки Dx* будет незначительной. Если неизвестный параметр а оценивают по одному числу 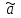 , то такую оценку называют точечной. Возможную ошибку, к которой может привести вычисление оценки , то такую оценку называют точечной. Возможную ошибку, к которой может привести вычисление оценки 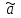 , по ограниченному числу измерений n, в математической статистике представляют с помощью доверительных интервалов и доверительных вероятностей. , по ограниченному числу измерений n, в математической статистике представляют с помощью доверительных интервалов и доверительных вероятностей.Пусть для параметра а получена из опыта несмещенная оценка 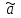 . Ясно, что оценка . Ясно, что оценка 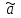 будет определять а тем точнее, чем меньше абсолютное значение их разности ε. Если задаться достаточно высокой вероятностью (например, β=0,9; 0,95 или даже 0,99, чтобы событие с такой вероятностью можно было считать практически достоверным) и найти такое значение ε, для которого будет определять а тем точнее, чем меньше абсолютное значение их разности ε. Если задаться достаточно высокой вероятностью (например, β=0,9; 0,95 или даже 0,99, чтобы событие с такой вероятностью можно было считать практически достоверным) и найти такое значение ε, для которого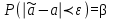 , (15) , (15)то диапазон возможных значений ошибки, возникающей от замены а на 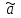 , будет ±ε. , будет ±ε.Большие по абсолютной величине ошибки могут появиться с очень малой вероятностью, которую называют степенью риска: а=1-β. (16) Заменив | 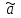 -а|<ε равносильным ему двойным неравенством -а|<ε равносильным ему двойным неравенством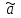 -ε<а< -ε<а<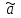 +ε, +ε,можно получить Р( 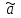 -ε<а< -ε<а<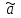 +ε)=β. (17) +ε)=β. (17)Это равенство означает, что с вероятностью β неизвестное значение параметра а попадает в интервал Jβ=( 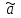 -ε, -ε, 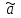 +ε). (18) +ε). (18)Вероятность β и интервал Jβ принято называть доверительными. Границы интервала также называют доверительными (рисунок 3).  Рисунок 3 – Доверительный интервал для оценки параметров Определение интервала, в который попадает случайная величина, как было отмечено ранее, требует знания ее закона распределения. Затруднение состоит в том, что закон распределения оценки зависит от закона распределения величины Х и, следовательно, от его неизвестных параметров (в частности, и от самого параметра а). Однако иногда удается найти некоторые функции от изучаемых параметров, закон распределения которых зависит только от числа опытов и вида закона распределения величины X. Так, английский математик В. Госсет, печатавшийся под псевдонимом Стьюдент, доказал, что при нормальном распределении случайной величины Х коэффициент распределенияtβ подчиняется закону с n-1 степенями свободы: 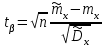 , (19) , (19)где 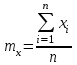 ; ; 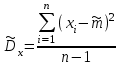 Дифференциальная функция этого закона имеет вид 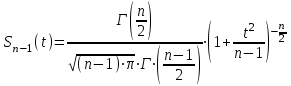 , (20) , (20)где Г(х) - гамма-функция. Этот закон впоследствии получил название распределения Стьюдента. С учетом уравнения (19) диапазон возможной ошибки 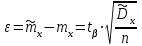 . (21) . (21)В таком случае доверительный интервал математического ожидания может быть определен как 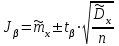 . (22) . (22)Коэффициент tβ находят по таблицам распределения Стьюдента (приложение А) в зависимости от принятого уровня доверительной вероятности и числа степеней свободы n-1. Известный английский статистик К.Пирсон нашел распределение величины Vx, являющейся функцией от действительного значения дисперсии Dх и ее оценки 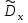 , полученной на основе анализа выборочных значений X: , полученной на основе анализа выборочных значений X: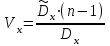 . (23) . (23)Оказалось, что величина Vx имеет χ2-распределение. Если найти Vx, то определение границ дисперсии Dx не вызывает затруднений. Плотность распределения f(Vx) имеет вид, изображенный на рисунке 4. Если бы
Но закон f(Vx) несимметричен, поэтому интервал Jβ обычно располагают так, чтобы вероятности выхода величины Vx за пределы интервала вправо и влево (заштрихованные площади на рисунке 4) были одинаковы, т. е. 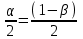 , (24) , (24)где α - принятый уровень риска. Чтобы построить интервал с такими свойствами, используют значения χ2 по таблице приложения Б в зависимости от числа степеней свободы k=n-1 и вероятности выхода за нижнюю Рниж или верхнюю Рверх границы, где 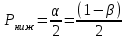 ; ; 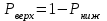 . .Затем определяют нижнюю и верхнюю границы возможных значений дисперсии 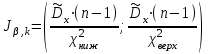 . (25) . (25)Пример. При измерении влажности зерна, поступившего на зерноочистительно-сушильный пункт, взято 5 проб, для которых получены следующие результаты: W1=22,l; W2=21,7; W3=23,4; W4=21,2; W5=22,7 %. Оценки числовых характеристик 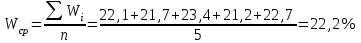 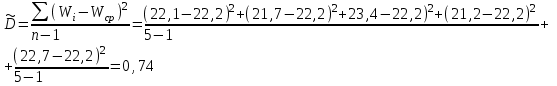 Доверительный интервал математического ожидания 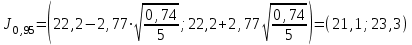 где tβ=2,77 принят по таблице приложения А для β=0,95 и k=n-1=4. Доверительный интервал дисперсии 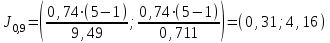 , ,где 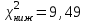 и и 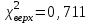 приняты по таблице приложения 3 для β=0,9 и k=n-1=4. приняты по таблице приложения 3 для β=0,9 и k=n-1=4.Из приведенного примера следует, что среднее значение изучаемой величины достаточно точно определяется даже при небольшом числе измерений, но судить о дисперсии в этом случае можно лишь с большой осторожностью, так как величина относительной ошибки очень велика. 2.2 Проверка статистических гипотез. Критерии согласия Любое предположение об изучаемой генеральной совокупности представляет собой статистическую гипотезу. Различают следующие статистические гипотезы: о законах распределения; о параметрах распределения и принадлежности тех или иных измерений, подозреваемых в ошибочной записи, к проверяемой выборке. Так, предположение о нормальном законе распределения размеров семян является гипотезой о законе распределения. Предположение о том, что средние расстояния между семенами, высеянными одинаковыми или однотипными высевающими аппаратами, различаются между собой, является гипотезой о параметрах распределения. При обработке опытных данных часто встречаются измерения, резко отличающиеся от остальных. В этом случае следует выяснить, что они собой представляют: экстремальные значения изучаемой величины или результат неверной записи, грубой ошибки при измерении, т. е. рассматривают гипотезу о принадлежности отдельных измерений к выборке. Проверку статистических гипотез осуществляют с помощью тех или иных критериев согласия. 2.3 Проверка гипотез о законе распределения Допустим, что на основе изучения вероятностей модели процесса выдвинута гипотеза о виде закона распределения f(x). Но после проведения эксперимента между теоретическим и фактическим рядами всегда неизбежны расхождения. Естественно, необходимо выяснить, чем вызваны эти различия: только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или обусловлены противоречием опытных данных выдвинутой гипотезе. Для этого используют так называемые критерии согласия: χ2 (К. Пирсона) и λ (А. Н. Колмогорова). Критерий К. Пирсона более надежный. Критерий А. Н. Колмогорова применяют в тех случаях, когда теоретический ряд был построен без опытных данных, т. е. даже числовые характеристики - параметры распределения определены теоретически. Схема использования критерия К. Пирсона состоит в следующем. Результаты опытов прежде всего сводят в К разрядов (классов) и оформляют в виде статистического ряда распределения с наблюдаемыми статистическими вероятностями 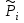 . .Используя теоретический закон распределения, можно найти теоретические значения вероятности попадания случайной величины в каждый из разрядов Pi. В качестве меры расхождения следует выбрать квадрат разности отклонений 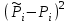 , взятых с некоторыми коэффициентами Сi: , взятых с некоторыми коэффициентами Сi: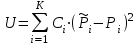 , (26) , (26)Коэффициенты Сi вводят потому, что в общем случае отклонения, относящиеся к различным разрядам, нельзя считать равноправными по значимости. Одно и то же по абсолютной величине отклонение может быть малозначимым, если сама вероятность велика, и, наоборот, очень значимым, если вероятность мала. Естественно, Сi следует брать обратно пропорционально вероятностям разрядов. Далее необходимо выбрать коэффициент пропорциональности. К. Пирсон показал, что если выбрать 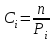 , (27) , (27)то при больших n закон распределения величины U практически не зависит от функции распределения F(x) и числа опытов n, а зависит главным образом от числа разрядов К и приближается к так называемому распределению χ2. При таком выборе коэффициентов мера расхождения 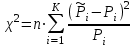 . (28) . (28)Если n ввести под знак суммы и учесть, что 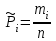 (здесь mi - число значений в i-м разряде), то (здесь mi - число значений в i-м разряде), то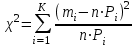 . (29) . (29)Распределение χ2 зависит от параметра k, называемого числом степеней свободы распределения, и определяемого как разность между числом разрядов К и числом наложенных связей. Для каждого значения χ2 и числа степеней свободы k по таблице приложения Б можно определить вероятность того, что за счет чисто случайных причин мера расхождения будет больше или равна вычисленному значению χ2. Если вероятность Р весьма мала (настолько, что событие с такой вероятностью можно считать практически невозможным), то результат опыта можно считать противоречащим гипотезе о том, что закон распределения величины Х есть F(x). Если Р достаточно велика, то выдвинутую гипотезу считают не противоречащей опытным данным. В качестве примера ниже приведены результаты сопоставления фактического распределения числа семян на участках длиной 5 см с теоретическим, рассчитанным по закону Пуассона с помощью критерия К. Пирсона.
Для данного примера 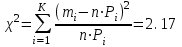 ; k=8-2=6; ; k=8-2=6; 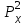 =0,9. =0,9.Расхождение между теоретическим и фактическим рядами распределения может быть обусловлено недостаточностью выборки. Вероятность Рх2 нельзя считать малой, поэтому можно сделать вывод, что экспериментальные данные не противоречат гипотезе о принятом распределении числа семян на отрезках 5 см длины рядка после посева их рядовой сеялкой. В качестве меры расхождения между теоретическим и фактическим распределениями по критерию А. Н. Колмогорова используют максимальное значение модуля разности между статистической и соответствующей теоретической функциями распределения (рис. 5).
А. Н. Колмогоров доказал, что при любой функции распределения F(x) и достаточно большом числе наблюдений вероятность неравенства 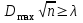 стремится к пределу 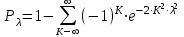 . .2.4 Проверка гипотез о параметрах распределения Поскольку в качестве основных параметров распределений случайных величин используют значения их математических ожиданий и дисперсий, то прежде всего важно сопоставить оценки этих числовых характеристик. Например, иногда результаты одной серии экспериментов значительно отличаются от результатов другой серии. Становится неясным, можно ли объяснить обнаруженное расхождение параметров случайными ошибками опыта или оно вызвано незамеченными или даже неизвестными закономерностями. В некоторых случаях, особенно при испытаниях модернизированных рабочих органов, получают результаты, которые мало отличаются от соответствующих показателей базовых машин. В этом случае следует определить существенность различий оценок параметров исследуемых распределений. Проверку существенности различий оценок математического ожидания проводят с помощью t-критерия. Для этого прежде всего определяют значение критерия 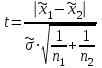 , (30) , (30)где 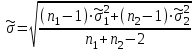 ; ; 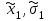 и и 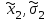 - оценки числовых характеристик coответственно первого и второго распределений; n1 и n2 - число измерений. - оценки числовых характеристик coответственно первого и второго распределений; n1 и n2 - число измерений.Затем по таблице приложения А находят критическое значение критерия Стьюдента в зависимости от числа степеней свободы k=n1+n2-2 и принятой доверительной вероятности 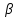 или соответствующего уровня риска α=1-β. Если t>tкp, то оценки математических ожиданий считают неоднородными, а при t<tкp разница между оценками несущественна. или соответствующего уровня риска α=1-β. Если t>tкp, то оценки математических ожиданий считают неоднородными, а при t<tкp разница между оценками несущественна.Пример 1. При сравнительных испытаниях серийной и экспериментальной зерноочистительных машин получены следующие значения степени отделения примесей, %: 94,3; 95,6; 92,7; 93,8; 94,8 – для серийной машины; 94,9; 95,3; 96,8; 97,5; 93,1 – для экспериментального образца. Определить существенность различий количеств отделения примесей сравниваемых устройств. Средние значения степени отделения примесей 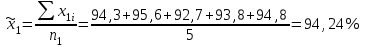 ; ;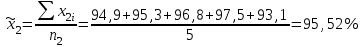 . .Оценки дисперсий 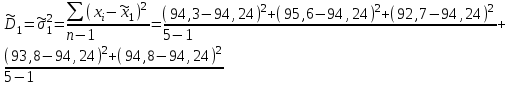 ; ;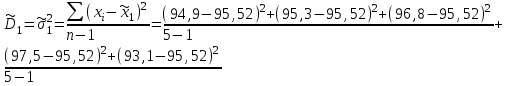 . .Следовательно, 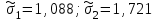 . .Среднее значение дисперсии 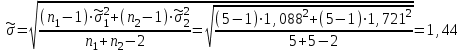 . .Критерий Стьюдента 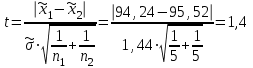 . .Критическое значение критерия Стьюдента для числа степеней свободы k=n1+n2-2=5+5-2=8 и принятого уровня риска α = 0,05 можно найти по таблице приложения А: tβкр=2,31. Поскольку tβ < tкр, то разницу в степени очистки семян испытуемыми зерноочистительными машинами можно считать несущественной. Существенность различий двух сравниваемых дисперсий проверяют с помощью критерия Фишера (F-критерия): 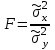 , (31) , (31)где 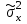 и и 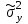 – соответственно большее и меньшее значения сравниваемых дисперсий. – соответственно большее и меньшее значения сравниваемых дисперсий.Далее по таблице приложения Г находят критическое значение критерия Фишера, соответствующее выбранному уровню риска α и числам степеней свободы k1=n1-1 и k2=n2-1. Если F< Fкp, то различие дисперсий считают несущественным. 3. Выбор числа наблюдений Существует много рекомендаций по выбору числа наблюдений n. С увеличением n уменьшается ошибка в определении оценок математического ожидания и дисперсии. Задаваясь допустимыми погрешностями этих величин, можно определить n. Но необходимое число измерений можно связать с точностью используемых измерительных средств. Например, если при измерении данным прибором ошибка равна δ, нет смысла уменьшать ее за счет увеличения числа замеров. Если из предварительных исследований известно ориентировочное значение 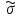 (найденное хотя бы по 15...25 измерениям), то вычисляют отношение (найденное хотя бы по 15...25 измерениям), то вычисляют отношение 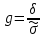 , а затем по этой величине и принятой надежности выборки α из таблицы 1 находят необходимое число измерений. , а затем по этой величине и принятой надежности выборки α из таблицы 1 находят необходимое число измерений.Таблица 1 – Необходимое число измерений
Если возможная ошибка не указана на шкале или в формуляре, то по значению ее можно принять равной минимальному делению шкалы прибора. Контрольные вопросы 1. Какие случайные величины относятся к дискретным и непрерывным? 2. Какими показателями характеризуются случайные величины? 3. Какими законами распределения описываются случайные величины? 4. Что понимают под доверительным интервалом? 5. В каких случаях применяют критерии Стьюдента и Фишера? 6. Как выбирают необходимое число наблюдений? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||