ммм. И с помощью Excel, сверить ответы. Проанализировать полученное оптимальное решение

Название	И с помощью Excel, сверить ответы. Проанализировать полученное оптимальное решение
Дата	16.02.2023
Размер	1.77 Mb.
Формат файла
Имя файла	ммм.docx
Тип	Решение #940293

В соответствии с номером варианта составить модель задачи линейного программирования, решить ее графически и с помощью Excel, сверить ответы. Проанализировать полученное оптимальное решение на чувствительность.

Компания производит полки для ванных комнат двух размеров – А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м² материала, а для полки типа В – 3 м² материала. Компания может получить до 1200 м² материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В – 30 мин; машину можно использовать 160 ч в неделю. Если прибыль от продажи полок типа А составляет 3 у. е., а от полок типа В – 4 у. е., то сколько полок каждого типа следует выпускать в неделю?

Решение:

Пусть х₁, х₂ – количество полок А и В (в шт).

Прибыль:

Ограничения на ресурсы:

Решаем графически:

Строим область допустимых значений:

Строим целевую функцию и двигаем ее в направлении вектора (3;4)

Итак, точка выхода из ОДЗ – точка пересечения прямых

. Определим ее координаты: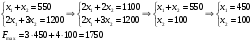

Итак, для получения максимальной прибыли в 1750 ден. ед. нужно производить 450 полок вида А и 100 полок вида В.
Решаем в MS Excel: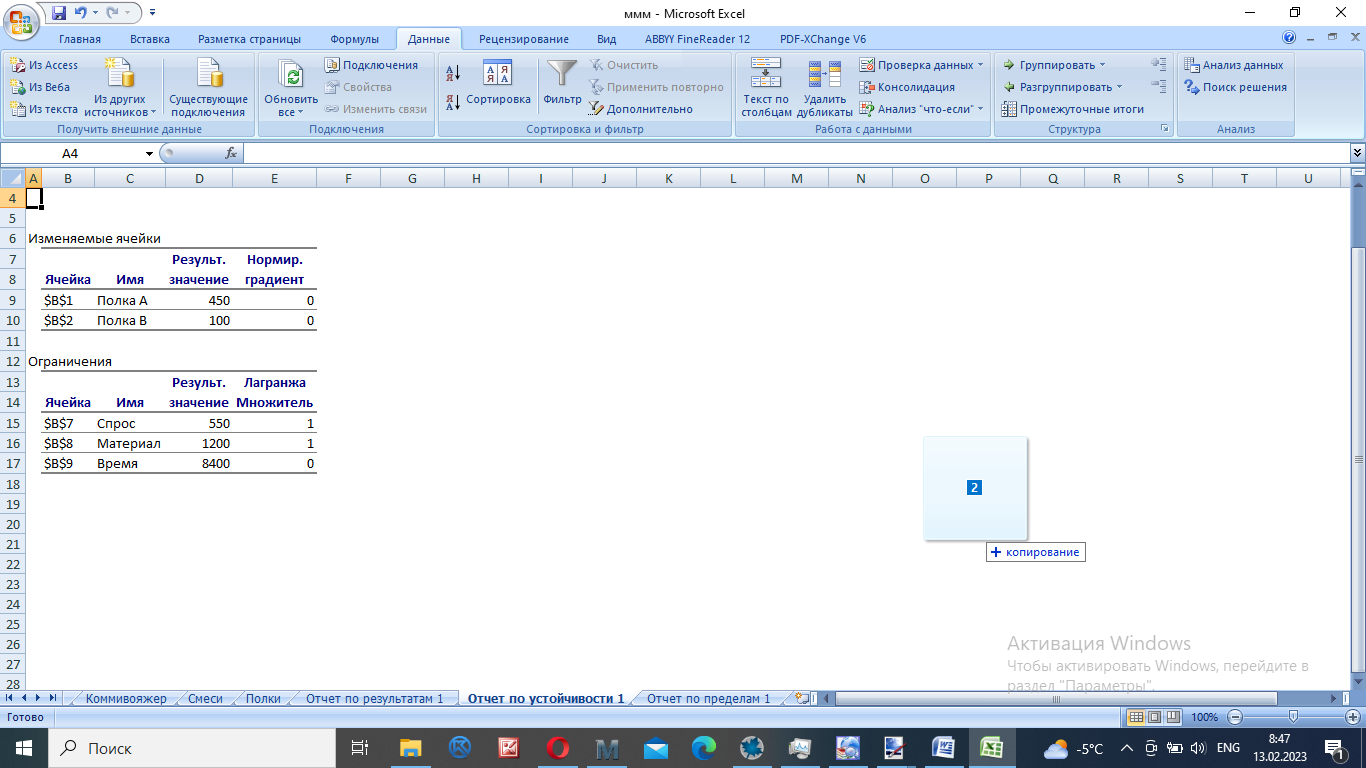

Выводы: оптимальные решения совпали. Проведем анализ:

Неизрасходованными остаются 18480 часов оборудования. Из этого следует, что запас недефицитного ресурса «Время» можно уменьшить на 18480 ч и это никак не повлияет на оптимальное решение. Допустимое увеличение цены на продукт А равно 1000 руб./шт., а допустимое уменьшение – 1450 руб./шт. Это означает, что если цена на продукт А возрастет более чем на 1000 руб./шт., то оптимальное решение изменится.

В соответствии с номером варианта составить модель задачи линейного программирования, решить ее с помощью Excel.

Пусть рациональное питание состоит из двух продуктов P и Q. Суточное питание этими продуктами должно давать не более 14 ед. жира (чтобы похудеть), но не менее 300 калорий. На упаковке продукта Р написано, что в 1 кг этого продукта содержится 15 ед. жира и 150 калорий, а на упаковке с продуктом Q – 4 ед. жира и 200 калорий соответственно. При этом цена 1 кг продукта Р равна 15 у. е., а 1 кг продукта Q – 25 у. е. В какой пропорции нужно брать эти продукты для того, чтобы выдержать условия диеты и истратить как можно меньше денег?

Решение:

Пусть х₁, х₂ – количество продуктов P и Q (в кг).

Стоимость рациона:

Ограничения на количество ингредиентов: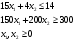

Решаем в MS Excel: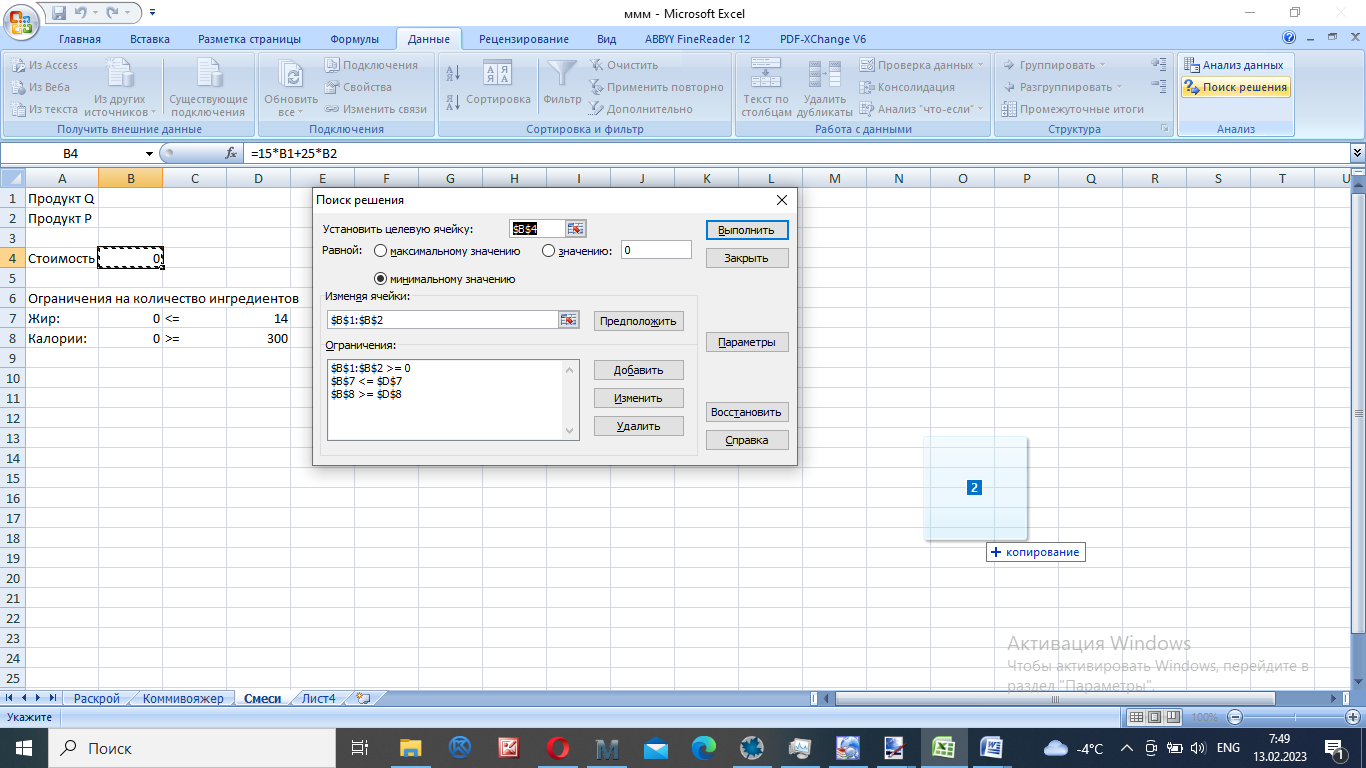

Итак, минимальная стоимость рациона 35 ден. ед., что включает в себя 2/3 кг продукта P и 1 кг продукта Q.
В соответствии с номером варианта составить модель задачи линейного программирования, решить ее с помощью Excel.

На производство поступил партия стержней длиной 250 и 190 см. Необходимо получить 470 заготовок длиной 120 см и 450 заготовок длиной 80 см. Отходы должны быть минимальными.

Решение:

Варианты раскроя вместе с получившимися остатками сведем в виде таблицы:

Вариант раскроя	Количество деталей			Отходы
	длины 120 см	длины 80 см
Раскрой стержня длиной 250 см
1	2	0	10
2	1	1	50
3	0	3	10
Раскрой стержня длиной 190 см
1	1	0	70
2	0	2	30

Для экономико-математической постановки рассматриваемой задачи введем следующие обозначения.

x_ij – количество заготовок i-го типа, раскроенных j-м способом (т. е. нам необходимо найти оптимальные x₁₁, x₁₂, x₁₃, x₂₁, x₂₂).

а_ijl – количество (целое число) деталей вида l, полученных при раскрое заготовки i-го типа j-м способом. В нашем случае: a₁₁₁ = 2, a₁₁₂ = 0, a₁₂₁ = 1, a₁₂₂ = 1, a₁₃₁ = 0, a₁₃₂ = 3, a₂₁₁ = 1, a₂₁₂ = 0, a₂₂₁ = 0, a₂₂₂ = 2. Таким образом, получаем: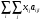

– общее количество деталей вида l;

c_ij – количество отходов при раскрое заготовок i-го типа j-м способом. В нашем случае: c₁₁ = 10, c₁₂ = 50, c₁₃ = 10, c₂₁ = 70, c₂₂ = 30.

b_i – количество заготовок i-го типа. В нашем случае ограничения по количеству заготовок не заданы.

Ограничения

на количество получаемых заготовок:

на неотрицательность переменных: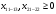

;

на целочисленность переменных:

- целые

Необходимо добавить ограничение, которое не позволяет одновременно всем переменным становится равным 0:

x₁₁ + x₁₂ + x₁₃ + x₂₁ + x₂₂ ≥ 1.

В итоге получаем экономико-математическую модель: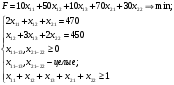

Решаем ее в MS Excel:

Таким образом, нужно взять только 385 стержней длиной 250 см и разрезать 235 из них по варианту раскроя 1 и 150 – по варианту раскроя 3.

В соответствии с номером варианта решить задачу коммивояжера.

Решение:

В диагональных клетках таблицы стоят значки ∞ (любое большое число, значительно превосходящее остальные числа в таблице), так как прямого маршрута между одноименными городами не существует. Коммивояжер, выезжая из города 1, должен посетить все города, побывав в каждом из них только по одному разу и вернуться в исходный город. Необходимо определить такой маршрут объезда городов, при котором длина маршрута будет минимальной.

Математическая модель:

Исходные данные и формулы для вычисления ограничений и целевой функции в рабочей книге MS Excel приведены на рис.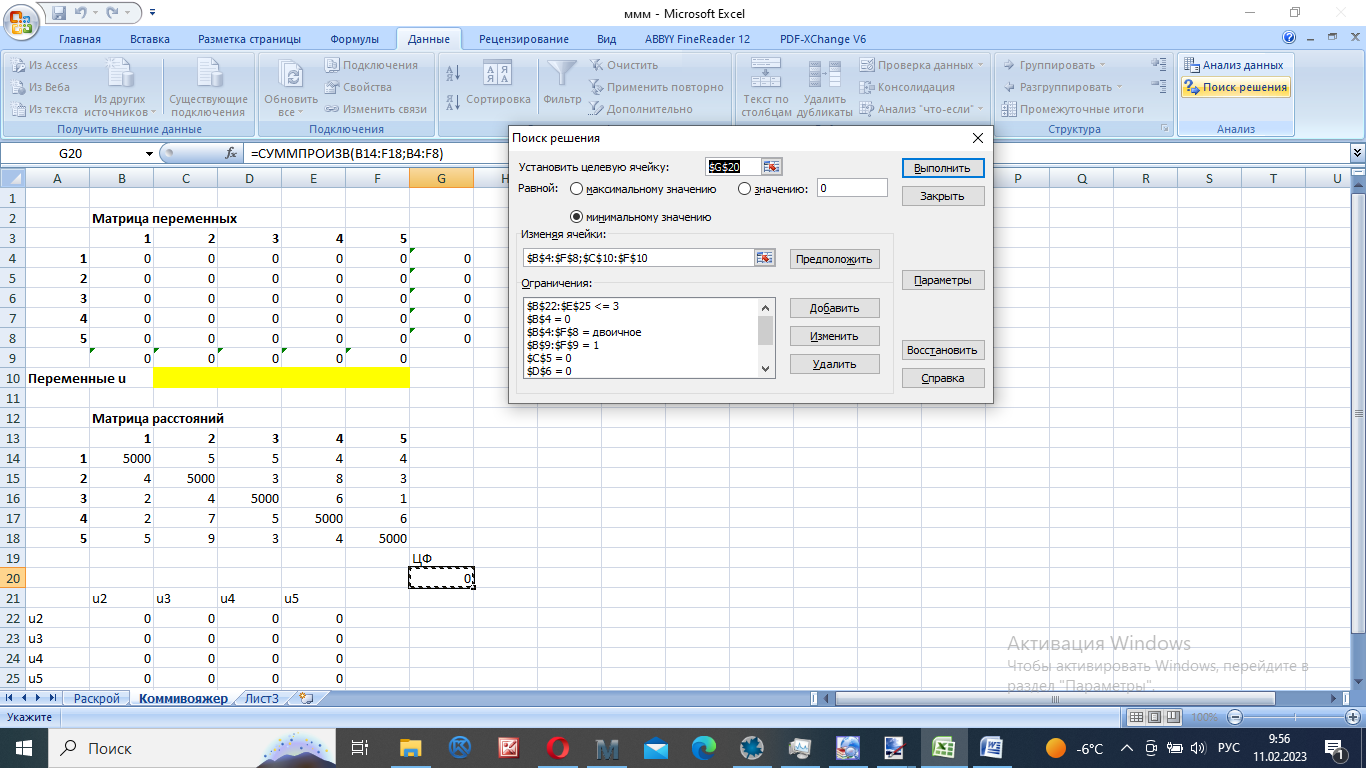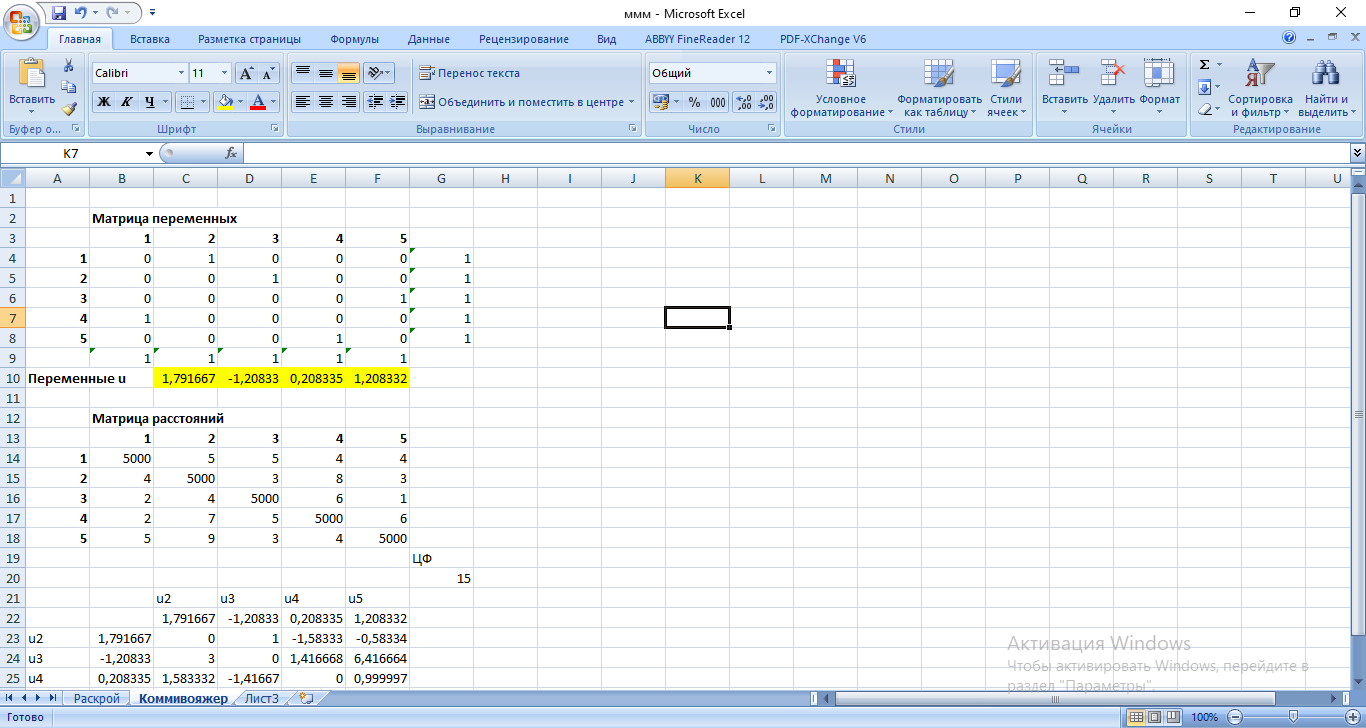

Итак, оптимальное решение таково: целевая функция F = 15, получившийся маршрут: 1 – 2 – 3 – 5 – 4 – 1.