физика по книге. I. Теория и задачи Механика Кинематика Теоретический материал
 Скачать 337.63 Kb. Скачать 337.63 Kb.
|
|
Часть I. Теория и задачи 1. Механика 1.1. Кинематика Теоретический материал Механическое движение. Относительность механического движения. В механике изучается наиболее простая форма движения – механическое движение. Механическим движением называется изменение положения данного тела (или его частей) относительно других тел, происходящее с течением времени. Любое механическое движение является относительным. В природе не существует абсолютного движения или абсолютного покоя. Поэтому для описания механического движения необходимо указать конкретное тело, относительно которого наблюдается движение других тел. Это тело называют телом отсчета. Таким образом, механическое движение – это изменение положения тел относительно выбранного тела отсчета. Материальная точка. Для математического описания движения в кинематике используются различные модели физических тел. Материальная точка – простейшая модель тела, используемая для описания движения в тех случаях, когда размерами и формой тела можно пренебречь. Эта модель применима, когда 1) размеры тела малы по сравнению с характерными размерами области движения тела или когда 2) твердое тело совершает поступательное движение (см. ниже). Положение материальной точки в пространстве определяется положением изображающей ее геометрической точки. Системой отсчета называют тело отсчета, связанную с ним систему координат и прибор для измерения времени (часы). Положение материальной точки в пространстве определяется тремя координатами 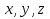 –Оно может быть задано также радиус-вектором –Оно может быть задано также радиус-вектором 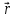 , r соединяющим начало координат с материальной точкой (рис. 1.1.1), причем , r соединяющим начало координат с материальной точкой (рис. 1.1.1), причем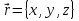 (1.1.1) (1.1.1) 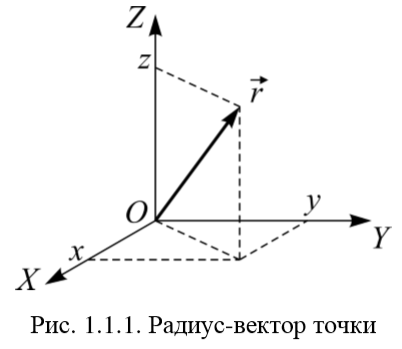 Единица измерения длины, установленная в Международной системе единиц (СИ), называется метром. Приближенно он равен 1/40000 000 части земного меридиана. По современному определению один метр – это расстояние, которое свет проходит в вакууме за 1/299792 458 долю секунды. Таким образом, определение единицы расстояния связано с определением единицы измерения времени – секундой. Одна секунда приближенно равна 1/86 400 доле земных суток. Для точных измерений времени используются атомные часы. Определенная в СИ секунда равна 9192 631770 периодам излучения атома цезия при переходе между двумя уровнями сверхтонкой структуры основного состояния. Траектория. При движении материальной точки конец радиус-вектора описывает в пространстве некоторую непрерывную линию, называемую траекторией точки. Уравнение, описывающее зависимость радиус-вектора движущейся точки от времени, 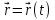 (1.1.2) (1.1.2)называется векторным кинематическим уравнением движения точки. Оно эквивалентно трем скалярным уравнениям движения: x x(t), y y(t), z z(t). (1.1.3) Траектории одной и той же точки в разных системах отсчета имеют, вообще говоря, различную форму. Кинематические уравнения движения точки в разных системах отсчета также различны. Перемещение материальной точки из положения 1 в положение 2 – это вектор 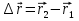 , (1.1.4) , (1.1.4)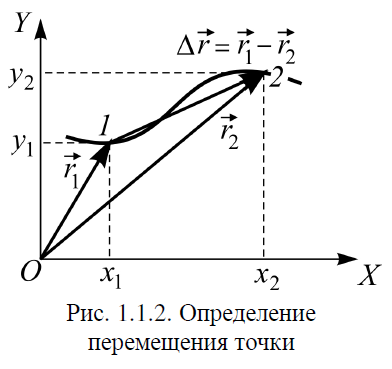 проведенный из начального положения точки в конечное (см. рис. 1.1.2). Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала: x x2 x1 , y y2 y1 , z z2 z1. (1.1.5) Эти величины часто называют перемещениями точки вдоль соответствующих координатных осей. Путь точки равен сумме расстояний, пройденных ею вдоль траектории, и всегда является неотрицательной величиной. Пути, пройденные точкой за последовательные промежутки времени, складываются арифметически. Модуль перемещения точки 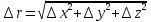 в общем случае не равен пути, пройденному точкой за данный промежуток времени. Эти величины совпадают только при движении точки по прямой в общем случае не равен пути, пройденному точкой за данный промежуток времени. Эти величины совпадают только при движении точки по прямойв одном направлении. Скорость. Средняя скорость точки в данной системе отсчета на интервале времени ( 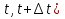 есть вектор есть вектор 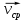 ,равный отношению вектора перемещения ,равный отношению вектора перемещения 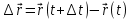 к величине интервала времени к величине интервала времени 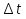 (рис 1.1.3): (рис 1.1.3):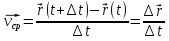 (1.1.6) (1.1.6)Направление средней скорости совпадает с направлением вектора перемещения 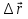 . .Средняя скорость характеризует движение точки в течение всего промежутка времени t, для которого она определена. 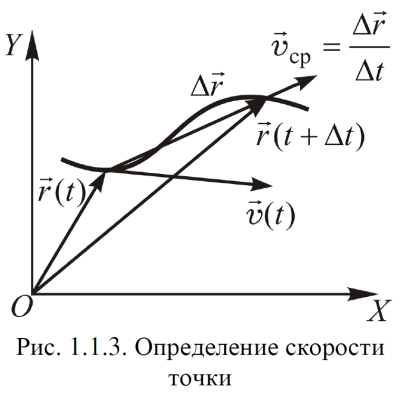 На практике часто используют понятие средней путевой скорости, которое определяют как отношение пути, пройденного точкой, ко времени его прохождения. Важно иметь в виду, что величина (мо-дуль) средней скорости в общем случае не совпадает со средней путевой скоростью. Они различны, например, при возвратно-посту-пательном движении по прямой, при криволинейном движении и т.п. Мгновенной скоростью (или просто скоростью) 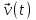 точки в данной системе отсчета в момент времени t называется предел средней скорости при неограниченном уменьшении интервала времени t : точки в данной системе отсчета в момент времени t называется предел средней скорости при неограниченном уменьшении интервала времени t :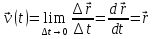 (1.1.7) (1.1.7)Компонентами вектора скорости являются производные по времени от компонент радиус-вектора точки: 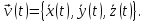 (1.1.8) (1.1.8)Вектор скорости направлен по касательной к траектории точки. Сложение скоростей. Важной задачей кинематики является ус-тановление связи между характеристиками движения точки отно-сительно разных систем отсчета. Пусть одна система отсчета, которую мы будем называть подвижной, движется поступательно со скоростью 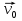 относительно другой системы, которую будем назы-вать неподвижной. Пусть скорость точки относительно подвижной системы отсчета равна относительно другой системы, которую будем назы-вать неподвижной. Пусть скорость точки относительно подвижной системы отсчета равна 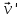 .Тогда скорость .Тогда скорость 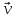 этой же точки относи-тельно неподвижной системы находится из соотношения, называе-мого законом сложения скоростей: этой же точки относи-тельно неподвижной системы находится из соотношения, называе-мого законом сложения скоростей: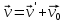 . (1.1.9) . (1.1.9)Ускорение. Среднее ускорение точки в данной системе отсчета на интервале времени (t, t t) есть вектор 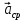 , равный отношению вектора приращения скорости , равный отношению вектора приращения скорости 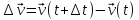 на этом интервале к величине интервала времени t (рис. 1.1.4): на этом интервале к величине интервала времени t (рис. 1.1.4):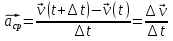 (1.1.10) (1.1.10) Мгновенным ускорением (или просто ускорением) точки 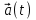 в момент времени t в данной системе отсчета называется предел среднего ускорения при стремлении интервала времени t к нулю: в момент времени t в данной системе отсчета называется предел среднего ускорения при стремлении интервала времени t к нулю: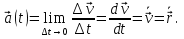 (1.1.11) (1.1.11)Сложение ускорений. Рассмотрим две системы отсчета: непод-вижную систему и систему, движущуюся поступательно и прямо-линейно относительно неподвижной с ускорением 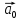 . Если уско-рение точки относительно подвижной системы отсчета равно . Если уско-рение точки относительно подвижной системы отсчета равно 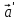 ,то ускорение ,то ускорение 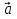 этой же точки относительно неподвижной системы на-ходится из соотношения, называемого законом сложения ускорений: этой же точки относительно неподвижной системы на-ходится из соотношения, называемого законом сложения ускорений: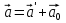 (1.1.12) (1.1.12)Прямолинейное равномерное и равнопеременное движения. По форме траектории движения делятся на прямолинейные и кри-волинейные. В первом случае траекторией движения точки в дан-ной системе отсчета является прямая линия, во втором случае – некоторая кривая. Для описания прямолинейного движения удобно совместить координатную ось (например, ось OX) с направлением, вдоль которого происходит движение. Равномерным называется движение с постоянной по модулю ско-ростью. При равномерном прямолинейном движении точки мгновен-ная скорость не зависит от времени и в каждой точке траектории направлена вдоль траектории. Средняя скорость за любой проме-жуток времени равна мгновенной скорости. Кинематическое урав-нение движения принимает вид 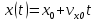 (1.1.13) (1.1.13)где x0 – начальная координата точки, vx0 – проекция скорости точки на координатную ось OX. Равнопеременное прямолинейное движение – это движение точки по прямой с постоянным по величине и по направлению ускоре-нием. При этом среднее ускорение равно мгновенному ускорению. Если направление ускорения 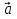 совпадает с направлением скорости точки, то движение называется равноускоренным, в противном случае –равнозамедленным. совпадает с направлением скорости точки, то движение называется равноускоренным, в противном случае –равнозамедленным.При равнопеременном прямолинейном движении зависимости ско-рости и координаты точки от времени выражаются следующими кинематическими уравнениями: 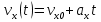 , , 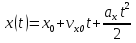 (1.1.14) (1.1.14)Зависимости скорости, координат и пути от времени. При решении задач и анализе результатов удобно представлять зави-симости координаты и скорости тела от времени графически. Примеры таких представлений для прямолинейного равномерного и равноускоренного движений приведены на рис. 1.1.5 и 1.1.6. 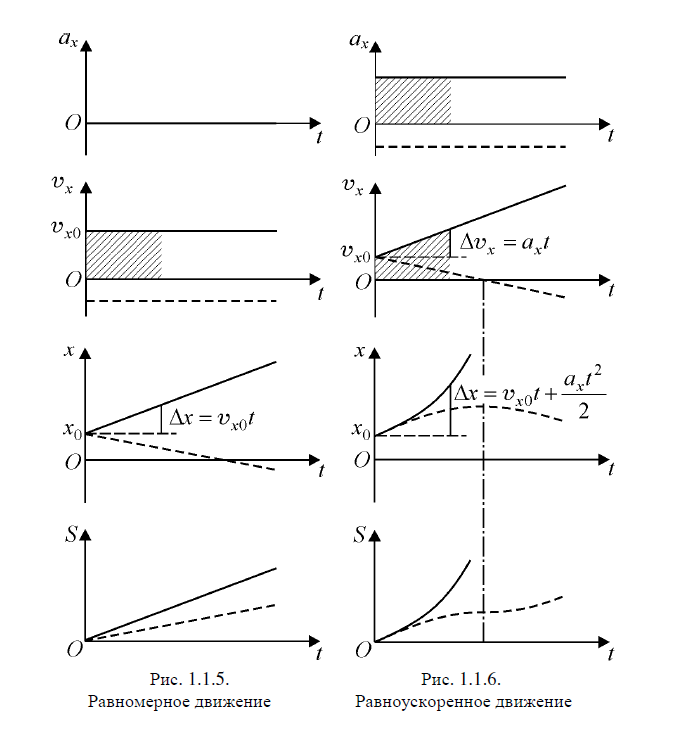 При построении графиков необходимо учитывать, что тангенс угла наклона касательной к кривой x x(t) в какой-либо момент времени пропорционален скорости точки в этот момент времени, а тангенс угла наклона касательной к кривой v v(t) пропорционален уско-рению точки в данный момент. По графику зависимости a a(t) можно найти изменение скорости за промежуток времени от t1 до t2 : оно равно площади под кривой a a(t) в пределах от t1 до t2. Аналогично по графику зависимости v v(t) можно найти изменение координаты точки за время (t2 t1). Криволинейное движение. Равномерное движение поокружности. Простейшей моделью криволинейного движения является равномерное движение по окружности. В этом случае точка движется по окружности с постоянной по величине скоростью v. Положение точки удобно описывать углом , который составляет радиус-вектор точки с некоторой фиксированной осью, например с осью ОX. Угловая скорость. Период и частота обращения. Величиной угловой скорости точки при движении по окружности называют отношение приращения угла поворота ее радиус-вектора ко времени t, за которое этот поворот произошел: 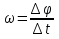 (см.рис. 1.1.7) (см.рис. 1.1.7)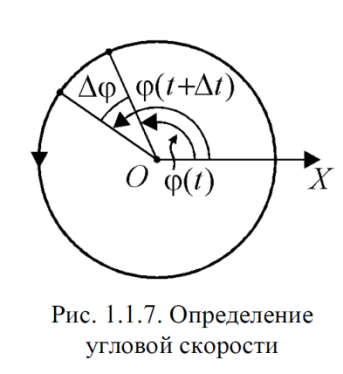 Периодом Т движения точки по окружности называют время, за которое точка совершает полный оборот. Частота обращения – это величина, обратная периоду. Угловая скорость, частота и пе-риод обращения при равномерном движении по окружности связа-ны между собой соотношениями: 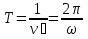 (1.1.15) (1.1.15)Линейная скорость v движения по окружности выражается через угловую скорость и радиус окружности R по формуле 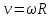 (1.1.16) (1.1.16)Ускорение тела при движении по окружности. При движении тела по окружности вектор скорости изменяется, поэтому у тела существует центростремительное ускорение, направленное по радиусу окружности к ее центру и по модулю равное 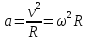 (1.1.17) (1.1.17)Для описания неравномерного движения по окружности используют величину 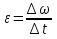 (1.1.18) (1.1.18)которая называется угловым ускорением. Тангенциальное и нормальное ускорение. При криволинейном движении точки часто бывает удобно разложить ее ускорение на две составляющие (рис. 1.1.8): 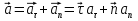 (1.1.19) (1.1.19)где 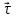 – единичный вектор, направленный по касательной к траектории в данной точке; – единичный вектор, направленный по касательной к траектории в данной точке;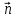 – единичный вектор по нормали к траектории, нап-равленный к центру кривизны. – единичный вектор по нормали к траектории, нап-равленный к центру кривизны.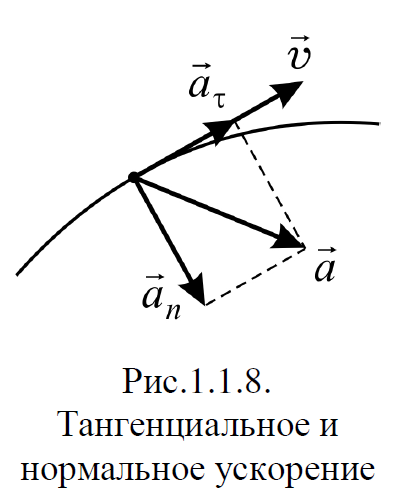 Составляющая 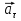 вектора ускорения, направленная по касатель-ной к траектории, называется тангенциальным (касательным) уско-рением. Тангенциальное ускорение характеризует изменение векто-ра скоростипо модулю. Вектор вектора ускорения, направленная по касатель-ной к траектории, называется тангенциальным (касательным) уско-рением. Тангенциальное ускорение характеризует изменение векто-ра скоростипо модулю. Вектор 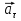 направлен в сторону движения точки при возрастании ее скорости и в противоположную сторону при убывании скорости. Составляющая направлен в сторону движения точки при возрастании ее скорости и в противоположную сторону при убывании скорости. Составляющая 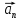 вектора ускорения, направленная по нормали к траектории в данной точке, называется нормальным ускорением. Нормальное ускорение характеризует изменение вектора скорости по направлению при криволинейном движении. вектора ускорения, направленная по нормали к траектории в данной точке, называется нормальным ускорением. Нормальное ускорение характеризует изменение вектора скорости по направлению при криволинейном движении.Модули тангенциального и нормального ускорения вычисляются по формулам 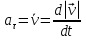 , ,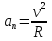 (1.1.20) (1.1.20)где R – радиус кривизны траектории в данной точке. При движении точки по окружности нормальное ускорение совпадает с центро-стремительным ускорением, а тангенциальное ускорение выра-жается через угловое ускорение по формуле aR. Свободное падение тел. Ускорение свободно падающего тела. Свободнымпадением называется движение, которое совершает тело только под действием притяжения Земли, без учета сопротивления воздуха. Ускорение 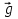 , с которым движется , с которым движетсявблизи поверхности Земли материальная точка, на которую дей-ствует только сила тяжести, называется ускорением свободного падения. Ускорение свободного падения не зависит от массы тела. Движение тела, брошенного под углом к горизонту. Даль-ность и высотаполета. При описании движения тела у поверх-ности Земли удобно выбрать системукоординат так, чтобы одна из координатных осей (обычно ось OX) была направленагоризонтально, а другая (обычно OY) – вертикально (рис. 1.1.9). Тогда движение пооси OX будет равномерным, а по оси OY – равнопеременным. В большинстве задачначало координат удобно совместить с точкой, откуда тело начинает движение. 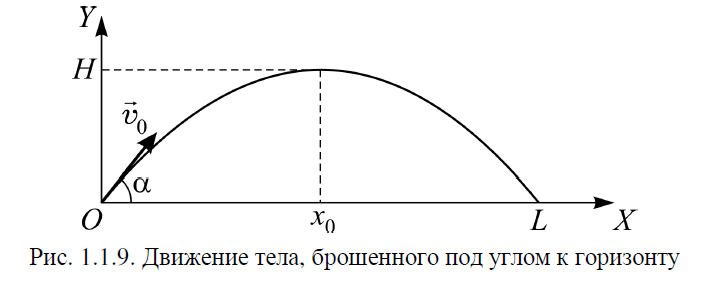 Для тела, брошенного от поверхности Земли со скоростью v0 под углом к горизонту, в системе координат, изображенной на рис. 1.1.9, 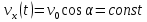 , ,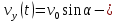 , (1.1.21) , (1.1.21)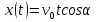 , ,  . (1.1.22) . (1.1.22)Исключая из уравнений (1.1.22) время t, получаем уравнение траектории тела 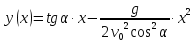 , (1.1.23) , (1.1.23)которое является уравнением параболы. В точке с координатой 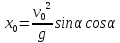 (1.1.24) (1.1.24)тело достигает наибольшей высоты 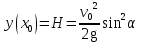 (1.1.25) (1.1.25)Величины 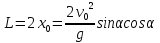 и и 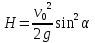 называются соответственно дальностью и высотой полета. называются соответственно дальностью и высотой полета.Поступательное и вращательное движения твердого тела. Твердое тело – это модель, применяемая в случаях, когда изменением формы и размеров тела приего движении можно пренебречь. Модель рассматривается как система материальных точек, расстояния между которыми остаются неизменными. Простейшие модели движения твердого тела – это поступательное и вращательное движения. Поступательным движением твердого тела (рис. 1.1.10) называют такое движение, при котором траектории всех точек тела одинаковы. При этом тело не поворачивается и каждая линия, соединяющая любые две точки тела, переносится параллель- но самой себе. При поступательном движении все точки тела в данный момент времени имеют одинаковые скорости и ускорения. Поэтому, зная движение какой-то одной точки тела, мы можем однозначно определить движение всех его остальных точек. Вращательным движением называется такое движение твердого тела, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой – оси вращения (рис. 1.1.11). Траектории всех точек лежат в плоскостях, параллельных друг другу и перпендикулярных оси вращения. 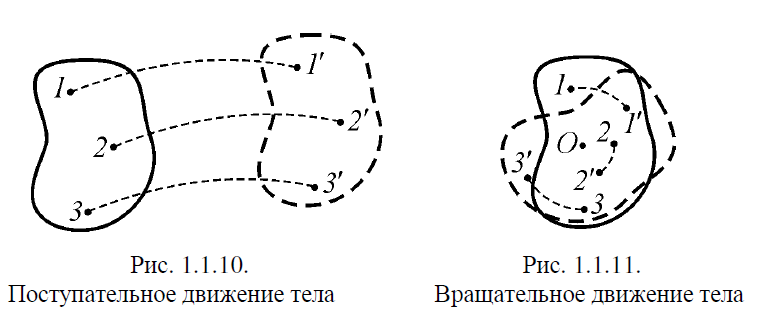 При таком движении различные точки тела за один и тот же промежуток времени проходят разные по длине пути. Линейная скорость v характеризует движение какой-либо одной точки тела, а не движение тела в целом. Поэтому для описания вращения тела используются такие величины, которые описывают движение всего тела, а не отдельных его точек. К этим величинам относятся: угол поворота , период вращения T, частота вращения 1/T, угловая скорость 2/T. Примеры решения задач Пример 1 . Пункты А и В находятся на берегу реки на некотором расстоянии друг от друга. Моторная лодка проходит расстояние АВ вниз по течению реки за время t1 3 ч, а плот то же расстояние – за время t0 12 ч. Какое время t2 затратит моторная лодка на обратный путь? |
