І топ. І топ. Сйкесін тап

• Название: І топ. Сйкесін тап
• Дата: 02.12.2021
• Размер: 65.6 Kb.
• Имя файла: І топ.docx
• Тип: Документы; #289284

І топ. Сәйкесін тап:

1. y=ax²+bx+c функциясының х осімен қиылысу нүктелері қалай табылады.	a0
2. Парабола төбесінің координаталары	D=b²-4·ac х1,2=
3. Парабола тармақтары төмен бағытталған	n= m=
4. Функцияның ең кіші мәнін табу неге байланысты	y=x² функциясының графигі (4;1) көшіріледі
5. y=(x-4)²+1функциясының графигін қалай алуға болады?	{0;4}
6. y=4x-x² функциясының х осімен қиылысу нүктесін табыңдар.	a
7. y=-x²+4x+3 қалай алуға болады.	y=-(x-2)²+7
8. y=-x²функциясының графигін 2 бірлік cолға жеті бірлік жоғары паралель көшіру арқылы қандай функция алуға болады.	y=-x² функциясының графигін (-2;7)

ІІ топ. Түсін мені...

у=х2 функциясының графигінің әр түрлі

орналасуы сызылған
1. Парабола (1) төбесінің координатын

жазыңдар.
2. Дискриминант (2) таңбасы қандай?
3. а-ның таңбасы (3) қандай?
4. (3) функцияның
формуласын жазыңдар.
5. (2) функцияның
формуласын жазыңдар.
6. (1) функцияның
формуласын жазыңдар.
ІІІ топ. Кім қырағы?..

Ғылымға қадам. Зерттеу есебі
Суретте қандай график бейнеленген. Графигі парабола болып табылатын функцияның қасиеттері туралы не білеміз?

Жауаптары:

х осімен қиылысуы	x=0,x=2 нүктеде функция 0-ге айналады.
Тармақтары	Парабола тармақтары төмен қараған
Қай аралықта функция оң, теріс мән қабылдайды.	x0,x функция мәндері теріс. 02 функция мәндері оң.
Симметрия осі	Симметрия осі х=1
Қай аралықта функция өспелі, кемімелі	x1 мәндерінде функция өспелі x1 мәндерінде функция кемімелі
Функцияның формуласы	y=-x(x-2)=2x-x²

Сергіту сәті

Тарихи мағлұмат (үй тапсырмасы)
1. Қозғалысы парабола болатын денелерге

мысал келтірейік.
а) Материалдық дене қозғалысы
б) Екінші космостың жылдамдық V=11,18 км/с.

Бұл жылдамдық параболалық деп аталады.

Себебі дене парабола бойымен қозғалады.

2. Қайда қолданылады?

а) Параболалық антенна

б) прожекторлар

в) телескоп

Аңыз: Сиракуз қаласының тұрғындары Сиракуз қаласын Параболлалық айнаның көмегімен Рим флотының шабуылынан қорғап қалған, сөйтіп Архимедтің құрастырған бронзадан жасаған параболалық антеннасының көмегімен 10-12 рим кемесін жағып жіберген.
Есептер шығару

Сыныпта: №272 (1), №273 (5), №276, №277
Үйге: №272 (2), №273 (3), №277 (2)

В: №272 (1)

Берілгені:

y=- x²+3 және y=x²+3х

Т/к: қиылысу нүктелерін

Шешуі: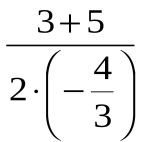

- x²+3 = x²+3х

- x²- x²-3х+3=0

-1 x²-3х+3=0

D=9-4·( )·3=9+16=250 2 түбірі бар.

х₁= =8: =-8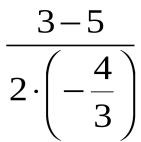· =-3 х₂= = =2· =

Жауабы: х₁=-3; х₂=


В: №273 (5)

Берілгені:

y=x²+3х+2 функцияның графигін салу керек.

Т/к:

1) Парабола төбесі коордиинаттарын табамыз:

m=- = =-1,5

n=(-1,5)²+3·(-1,5)+2=-0,25

Парабола төбесі (-1,5; -0,25) нүктесі болады.
2) х=-1,5 арқылы 0у осіне параллель түзу жүргіземіз.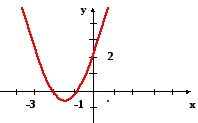




3) Оу осімен қиылысу нүктесін табамыз.

х=0 у=0²+3·0+2=2 (0; 2)

0х осімен қиылысу нүктесін табамыз.

у=0 х²+3х+2=0 теңдеуін шешеміз

D=9-4·2=1

х_{1= =}-2 х₂= ₌-1 (-2; 0) (-1; 0)
4) х=-1,5 нүктесіне қарағанда х=0 нүктесі

х=-3 нүктесіне симметриялы

у(0)= у(3)=2

С: №276

Берілгені: Квадраттық функция

у=2х²+4х-6 мына тапсырмаларды орындаңдар.

1. 
   функцияны у=а(х-m)²+n түріне келтіру керек:
   

y=2(x²+2x-3)=2(x+1)²-4

1. 
   парабола төбесінің координаталары анықтаймыз.
   

x=- = =1

y=2·(-1)²+4·(-1)-6=-8 (-1;8)

1. 
   функцияның нольдерін табамыз.
   

х=0 y=-6 (0; 6)

y=0 2х²+4х-6=0

D=16-4·2·(-6)=64

х₁==1 х₂==-3 (-3; 0) (1; 0)

1. 
   Функцияның ең кіші мәнін есептейміз.
   

Симметрия осі х=-1 у=-8 ең кіші мәні

1. 
   (-; -1) аралықта функция кемиді
   

(-1; +) аралықта функция өседі.

С: №277

у=|х²+х-2|

1. 
   у=х² графигін саламыз.
   
2. 
   Парабола төбесін анықтаймыз
   

(-0,55; -1,25)

1. 
   Параболаның төбесін (-0,5; -1,25) нүктесіне көшіреміз.
   

m=- ==-0,5

n==-2,25

1. 
   0х осімен қиылысу нүктелерін анықтаймыз.
   

D=1-4·(-2)=9

х₁==-2 х₂==1

1. 
   Модуль болғандықтан графиктің (-0,5; -1,25) аралығын оң жарты жазыққа көшіреміз.