И.В.Черных. Simulink. И. В. Черных. "Simulink Инструмент моделирования динамических систем"
 Скачать 3.7 Mb. Скачать 3.7 Mb.
|
|
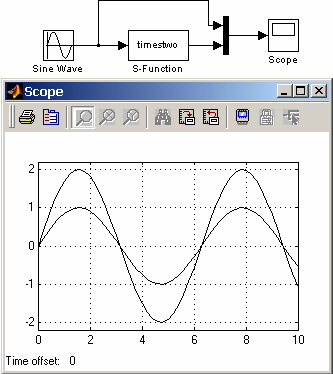
% Расчет значения времени для следующей расчетной точки дискретной % % части системы % %==================================================================% case 4, sys=mdlGetTimeOfNextVarHit(t,x,u); %====================% % Завершение расчета % %====================% case 9, sys=mdlTerminate(t,x,u); %======================================% % Неизвестное значение переменной flag % %======================================% otherwise error(['Unhandled flag = ',num2str(flag)]); end % Окончание функции sfuntmpl %===============================================================% % mdlInitializeSizes % % Функция инициализации % % Расчет начальных условий, значений вектора модельного времени,% % размерности матриц % %===============================================================% function [sys,x0,str,ts]=mdlInitializeSizes % Приведенные ниже значения параметров даны в качестве примера и не отражают % реально задаваемых значений. sizes = simsizes; % Первый вызов функции simsizes создает структуру sizes sizes.NumContStates = 0; % Число непрерывных переменных состояния sizes.NumDiscStates = 0; % Число дискретных переменных состояния sizes.NumOutputs = 0; % Число выходных переменных (размерность выходного % вектора) sizes.NumInputs = 0; % Число входных переменных (размерность вектора u) sizes.DirFeedthrough = 1; % Параметр, задающий проход входного сигнала на % выход. % Этот параметр нужно задавать равным 1, в том % случае, если входной сигнал прямо или % опосредованно(например, через логическое % выражение или алгебраическую операцию) % проходит на выход системы (иными словами: если % входной сигнал u, входит в выражения задаваемые в % функции mdlOutputs) или используется метод % mdlGetTimeOfNextVarHit. % При описании системы в уравнениях пространства % состояний этот параметр следует задать равным 1, % если матрица D (матрица обхода) не пустая и % равным нулю, в противном случае. sizes.NumSampleTimes = 1; % Размерность вектора модельного времени. % Минимальное значение параметра = 1 % (одна строка в матрице ts). sys = simsizes(sizes); % Второй вызов функции simsizes. Данные о % размерностях передаются в Simulink. x0 = []; % Задание вектора начальных значений переменных состояния % (начальных условий). str = []; % Задание параметра str, как пустой матрицы. Параметр % заразервирован для будущего использования. ts = [0 0]; % Матрица из двух колонок, задающая шаг модельного времени % и смещение. % Окончание mdlInitializeSizes %========================================================================% % mdlDerivatives % % Функция для расчета значений производных вектора состояния непрерывной % % части системы % %========================================================================% function sys=mdlDerivatives(t,x,u) sys = []; % Окончание mdlDerivatives %==========================================================================% % mdlUpdate % % Функция для расчета значений вектора выходных сигналов непрерывной части % % системы % %==========================================================================% function sys=mdlUpdate(t,x,u) sys = []; % Окончание mdlUpdate %===========================================================================% % mdlOutputs % % Функция для расчета значений вектора выходных сигналов непрерывной части % % системы % %===========================================================================% function sys=mdlOutputs(t,x,u) sys = []; % Окончание mdlOutputs %===========================================================================% % mdlGetTimeOfNextVarHit % % Расчет значения времени для следующей расчетной точки дискретной части % % системы. % % Функция рассчитывает время (абсолютное значение), по достижении которого % % значения дискретной части системы передаютсяв Simulink-модель. % % Функция используется только в случае моделирования дискретной части % % системы с переменным шагом (variable discrete-time sample time). В этом % % случае параметр ts функции mdlInitializeSizes должен быть задан как [-2 0]% %===========================================================================% function sys=mdlGetTimeOfNextVarHit(t,x,u) sampleTime = 1; % Пример: время срабатывания блока увеличивается % на 1 секунду. sys = t + sampleTime; % Окончание mdlGetTimeOfNextVarHit %=========================================% % mdlTerminate % % Функция, выполняющая завершение расчета % %=========================================% function sys=mdlTerminate(t,x,u) sys = [];% Окончание mdlTerminate [Скачать пример] 16.7. Примеры S-функций языке MATLAB 16.7.1. Простейшая S-функция Одним из самых простых примеров S-функций поставляемых с пакетом MATLAB является функция timestwo (файл timestwo.m). Данная S-функция выполняет умножение входного сигнала на коэффициент 2. Ниже приведен текст этой S-функции. function [sys,x0,str,ts] = timestwo(t,x,u,flag) % % TIMESTWO - Пример S-функции. Выходной сигнал равен входному, % умноженному на 2: % y = 2 * u; % % Шаблон для создания S-функции - файл sfuntmpl.m . % % Copyright 1990-2001 The MathWorks, Inc. % $Revision: 1.6 $ % Авторский перевод комментариев: Черных И.В. % switch flag, % В зависимости от значения переменной flag происходит % вызов того или иного метода: %===============% % Инициализация % %===============% case 0 [sys,x0,str,ts]=mdlInitializeSizes; %===========================================% % Расчет значений вектора выходных сигналов % %===========================================% case 3 sys=mdlOutputs(t,x,u); %=========================================% % Неиcпользуемые значения переменной flag % %=========================================% % В примере не используются методы для завершения работы S-функции, % нет непрерывных и дискретных переменных состояния, % поэтому значения переменной flag = 1, 2, 4, 9 не используются. % Результатом S-функции в этом случае является пустая матрица. case { 1, 2, 4, 9 } sys=[]; %======================================% % Неизвестное значение переменной flag % %======================================% otherwise error(['Unhandled flag = ',num2str(flag)]); end % Окончание функции timestwo %===============================================================% % mdlInitializeSizes % % Функция инициализации % % Расчет начальных условий, значений вектора шагов модельного % % времени, размерности матриц % %=============================================================% % function [sys,x0,str,ts] = mdlInitializeSizes() sizes = simsizes; sizes.NumContStates = 0; % Число непрерывных переменных состояния. sizes.NumDiscStates = 0; % Число дискретных переменных состояния. sizes.NumOutputs = -1; % Число выходных переменных (размерность выходного вектора). % Динамическая размерность выходного вектора. sizes.NumInputs = -1; % Число входных переменных (размерность входного % вектора). % Динамическая размерность входного вектора. sizes.DirFeedthrough = 1; % Прямой проход. Есть проход входного сигнала % на выход. sizes.NumSampleTimes = 1; % Размерность вектора шагов модельного времени. sys = simsizes(sizes); str = []; % Параметр заразервирован для будущего % использования. x0 = []; % Задание вектора начальных значений переменных % состояния. % Переменных сомтояния нет, поэтому значение % параметра - пустая матрица. ts = [-1 0]; % Матрица из двух колонок, задающая шаг % модельного времени и смещение. % Шаг наследуется из предшествуюшего блока. % Окончание mdlInitializeSizes % %========================================================% % mdlOutputs % % Функция для расчета значений вектора выходных сигналов % %========================================================% % function sys = mdlOutputs(t,x,u) sys = u * 2; % Выходной сигнал блока есть входной сигнал, умноженный на % коэффициент 2. % Окончание mdlOutputs Пример модели с S-функцией timestwo приведен на рис.16.4.
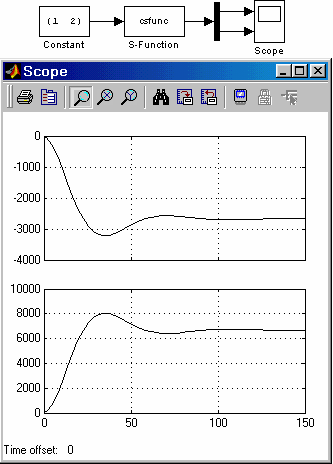
[Скачать пример] 16.7.2. Модель непрерывной системы Модель непрерывной системы, описываемой уравнениями пространства состояния дана в файле csfunc.m . Данная S-функция моделирует непрерывную систему с двумя входами, двумя выходами и двумя переменными состояния. Параметры модели (значения матриц A,В,С,D) задаются в теле S-функции и передаются в callback-методы через их заголовки в качестве дополнительных параметров. Ниже приведен текст этой S-функции. S-функция csfunc: function [sys,x0,str,ts] = csfunc(t,x,u,flag) % CSFUNC Пример S-функции. Спомощью уравнений пространства состояния % моделируется непрерывная система: % % x' = Ax + Bu % y = Cx + Du % % Значения матриц передаются в callback-методы через их заголовки % в качестве дополнительных параметров % % % Шаблон для создания S-функции - файл sfuntmpl.m . % % Copyright 1990-2001 The MathWorks, Inc. % $Revision: 1.8 $ % Авторский перевод комментариев: Черных И.В. % Задание матриц: A=[-0.09 -0.01 1 0]; % Mатрица системы. B=[ 1 -7 0 -2]; % Mатрица входа. C=[ 0 2 1 -5]; % Mатрица выхода. D=[-3 0 1 0]; % Mатрица обхода. switch flag, % В зависимости от значения переменной flag происходит % вызов того или иного метода: %===============% % Инициализация % %===============% case 0, [sys,x0,str,ts]=mdlInitializeSizes(A,B,C,D); %====================% % Расчет производных % %====================% case 1, sys=mdlDerivatives(t,x,u,A,B,C,D); %===========================================% % Расчет значений вектора выходных сигналов % %===========================================% case 3, sys=mdlOutputs(t,x,u,A,B,C,D); %=========================================% % Неиcпользуемые значения переменной flag % %=========================================% % В примере не используются методы для завершения работы S-функции, % нет дискретных переменных состояния, % поэтому значения переменной flag = 2, 4, 9 не используются. % Результатом S-функции в этом случае является пустая матрица. case { 2, 4, 9 } sys=[]; %======================================% % Неизвестное значение переменной flag % %======================================% otherwise error(['Unhandled flag = ',num2str(flag)]); end % Окончание csfunc % %===============================================================% % mdlInitializeSizes % % Функция инициализации % % Расчет начальных условий, значений вектора модельного времени,% % размерности матриц % %===============================================================% % function [sys,x0,str,ts]=mdlInitializeSizes(A,B,C,D) sizes = simsizes; sizes.NumContStates = 2; % Число непрерывных переменных состояния. sizes.NumDiscStates = 0; % Число дискретных переменных состояния. sizes.NumOutputs = 2; % Число выходных переменных (размерность выходного % вектора). sizes.NumInputs = 2; % Число входных переменных (размерность входного % вектора). sizes.DirFeedthrough = 1; % Прямой проход. Есть проход входного сигнала % на выход. % (матрица D не пустая). sizes.NumSampleTimes = 1; % Размерность вектора шагов модельного времени. sys = simsizes(sizes); x0 = zeros(2,1); % Задание вектора начальных значений переменных % состояния. Начальные условия нулевые. str = []; % Параметр заразервирован для будущего % использования. ts = [0 0]; % Матрица из двух колонок, задающая шаг модельного % времени и смещение. % Окончание mdlInitializeSizes % %========================================================================% % mdlDerivatives % % Функция для расчета значений производных вектора состояния непрерывной % % части системы % %========================================================================% % function sys=mdlDerivatives(t,x,u,A,B,C,D) sys = A*x + B*u; % Окончание mdlDerivatives % %========================================================% % mdlOutputs % % Функция для расчета значений вектора выходных сигналов % %========================================================% function sys=mdlOutputs(t,x,u,A,B,C,D) sys = C*x + D*u; % Окончание mdlOutputs Пример модели с S-функцией csfunc приведен на рис.16.5.
[Скачать пример] 16.7.3. Модель дискретнойной системы Модель дискретной системы, описываемой уравнениями пространства состояния, дана в файле dsfunc.m . Данная S-функция моделирует дискретную систему с двумя входами, двумя выходами и двумя переменными состояния. Параметры модели (значения матриц A, В, С, D) задаются в теле S-функции и передаются в callback-методы через их заголовки в качестве дополнительных параметров. Ниже приведен текст этой S-функции. S-функция dsfunc: function [sys,x0,str,ts] = dsfunc(t,x,u,flag) % DSFUNC Пример S-функции. С помощью уравнений пространства состояния % моделируется дискретная система: % x(n+1) = Ax(n) + Bu(n) % y(n) = Cx(n) + Du(n) % % Значения матриц передаются в callback-методы через их заголовки % в качестве дополнительных параметров % % Шаблон для создания S-функции - файл sfuntmpl.m . % % Copyright 1990-2001 The MathWorks, Inc. % $Revision: 1.8 $ % Авторский перевод комментариев: Черных И.В. % Задание матриц: |