Расчет резервуара. И в перемещениях для осесимметричной задачи теории упругости, общее решение
 Скачать 0.95 Mb.
|
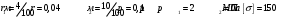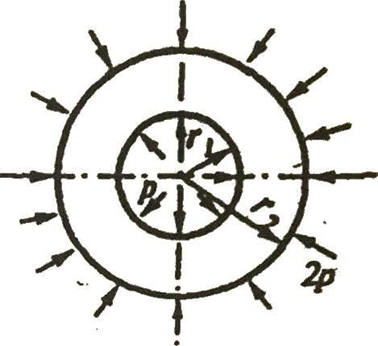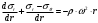 Исходные данные Критерий-Мизеса Решение Привести уравнения равновесия в напряжениях и в перемещениях для осесимметричной задачи теории упругости, общее решение задачи в перемещениях и напряжениях. У  равнение равновесия в напряжениях Уравнение равновесия в перемещениях 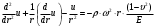 Общее решение задачи в перемещениях 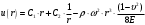 Общее решение задачи в напряжениях 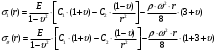 C1, C2, – постоянные интегрирования, определяемые из граничных условий 1 Запишем формулу Ламе 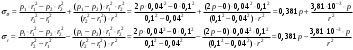 Построение эпюр 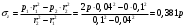 осевые н напряжения(действуют так как сосуд закрытый) Внутренняя поверхность трубы: 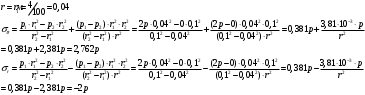 Наружная поверхность трубы: 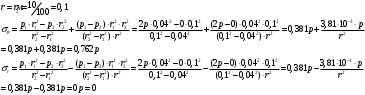 По полученным значениям строим эпюры (рис2) Запишем условие прочности используя Критерий-Мизеса 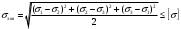 Главные напряжения На внутренней поверхности трубы 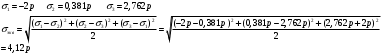 На внешней поверхности трубы 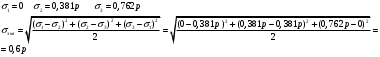 Опасные точки на ВНУТРЕННЕЙ поверхности трубы 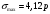 Условие прочности 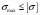 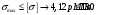 Отсюда допускаемая нагрузка 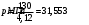 Построение Эпюр Внутренняя поверхность трубы: 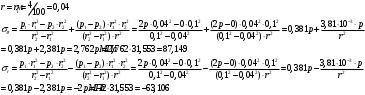 Наружная поверхность трубы: 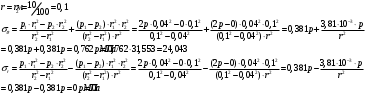 Радиальное перемещение u точки стенки, отстоящей от оси цилиндра на расстояние r определяется по формуле: 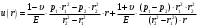 Внутренняя поверхность трубы: 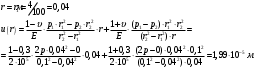 Середина стенки трубы: 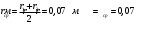 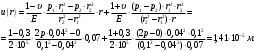 Наружная поверхность трубы: 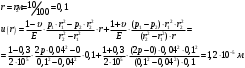 Построим эпюры радиальных и меридиональных напряжений, а также радиальных перемещений u (Рис.2 ) 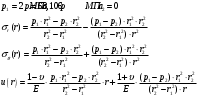  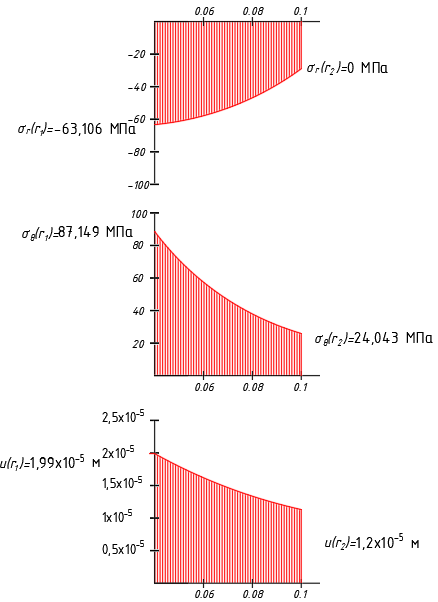 Рис 2 Изобразим элемент вырезанный в опасной точке (рис3) 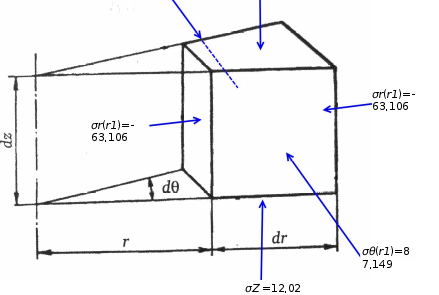 σθ(r1)=87.149 σZ=12.02 Рис 3 |