Идз 1 Вариант 14 Вычислить определенные интегралы с точностью до двух знаков после запятой
 Скачать 213.5 Kb.
|
|
ИДЗ 9.1 – Вариант 14 1. Вычислить определенные интегралы с точностью до двух знаков после запятой. 1.14  Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная той функции на [a,b], то определенный интеграл от функции f(x) на [a,b] равен приращению первообразной на этом отрезке:  Используем в решении формулу половинного угла  Вычисляем определенный интеграл  2.14  Пусть функции u=u(x) и v=v(x) имеют непрерывные производные на [α, β], тогда  , где  Пусть u = x2, тогда dv = sin4xdx, du = (x2)′dx = 2xdx,   Учли, в нахождении v, табличный интеграл  Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная той функции на [a,b], то определенный интеграл от функции f(x) на [a,b] равен приращению первообразной на этом отрезке: Запишем интеграл  Снова применим метод интегрирования по частям Пусть u = x, тогда dv = cos4xdx, du = (x)′dx = dx,  Решаем определенный интеграл 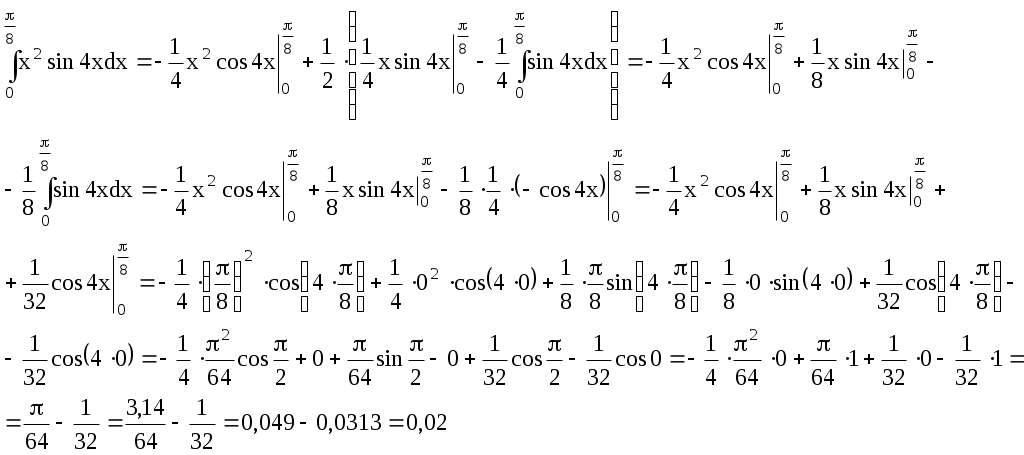 3.14  Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная той функции на [a,b], то определенный интеграл от функции f(x) на [a,b] равен приращению первообразной на этом отрезке: Разделив числитель подынтегральной функции на знаменатель, выделим целую часть неправильной дроби, стоящей под знаком интеграла. Получим интеграл от алгебраической суммы:  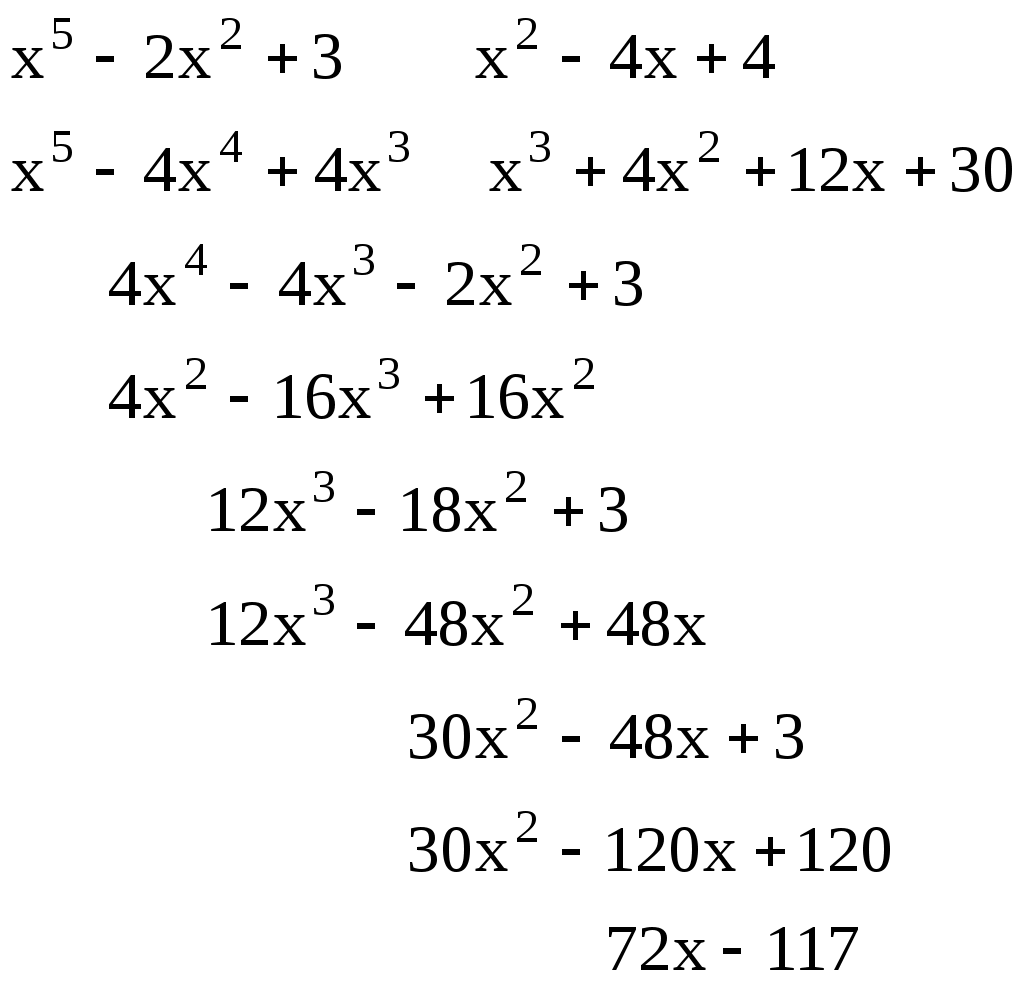 Разложили квадрат разности   Запишем интеграл и разложим подынтегральное выражение на простейшие дроби:  (1)Отсюда  Найдем значения коэффициентов A, B при x = 2  при x = 0  Подставляем в выражение (1), найденные значения коэффициентов А, В получаем решение исходного интеграла: 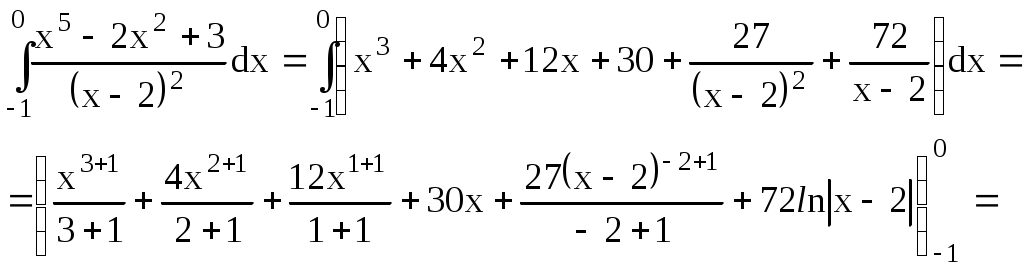  4.14  Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная той функции на [a,b], то определенный интеграл от функции f(x) на [a,b] равен приращению первообразной на этом отрезке: Интегрирование заменой переменной (метод подстановки)  Проведем замену:  и t = arctgx,Запишем пределы интегрирования для переменной t при  при  Вычисляем определенный интеграл 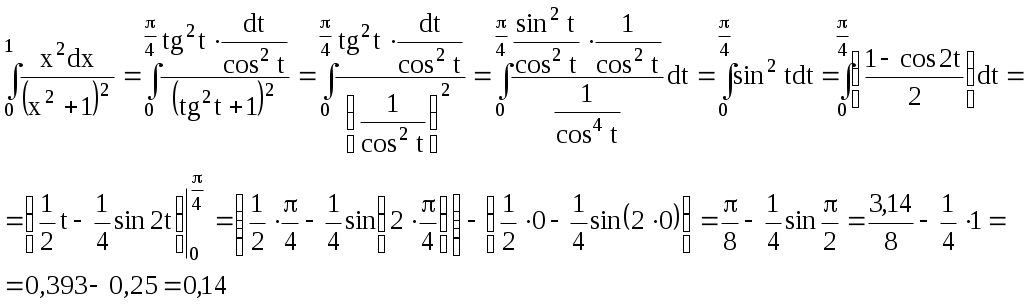 Учли в решении интеграла тригонометрическое тождество  ,  и формулу половинного угла  5.14  Используя формулу произведения тригонометрических функций  , преобразуем подынтегральное выражение  Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная той функции на [a,b], то определенный интеграл от функции f(x) на [a,b] равен приращению первообразной на этом отрезке: Решаем определенный интеграл 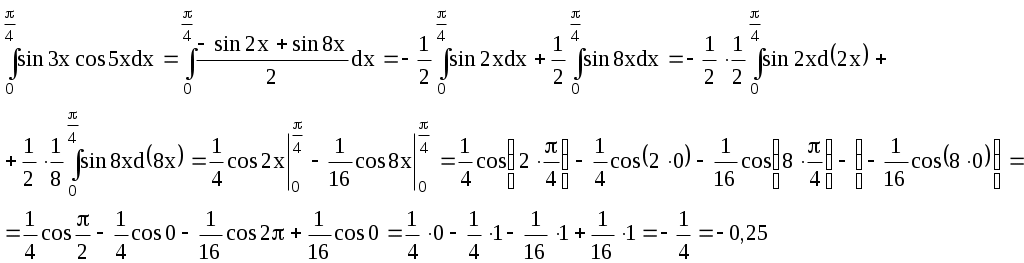 6.14  Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная той функции на [a,b], то определенный интеграл от функции f(x) на [a,b] равен приращению первообразной на этом отрезке: Представим данный интеграл в виде суммы двух интегралов, предварительно выделив в числителе подынтегральной функции слагаемое, равное производной подкоренного выражения из знаменателя:  Решение первого интеграла:  Решение второго интеграла Применима табличная формула интегрирования  Преобразуем интеграл, выделим в знаменателе подынтегральной функции полный квадрат (формула квадрата разности (a − b)2 = a2 − 2ab + b2)  Тогда запишем интеграл  Вычисляем определенный интеграл 7.14  Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) – любая первообразная той функции на [a,b], то определенный интеграл от функции f(x) на [a,b] равен приращению первообразной на этом отрезке: Интегрирование заменой переменной (метод подстановки): Проведем замену:  , отсюда  , Запишем пределы интегрирования для переменной t при  ; при  тогда запишем промежуточное решение  Разделив числитель подынтегральной функции на знаменатель, выделим целую часть неправильной дроби, стоящей под знаком интеграла. Получим интеграл от алгебраической суммы: 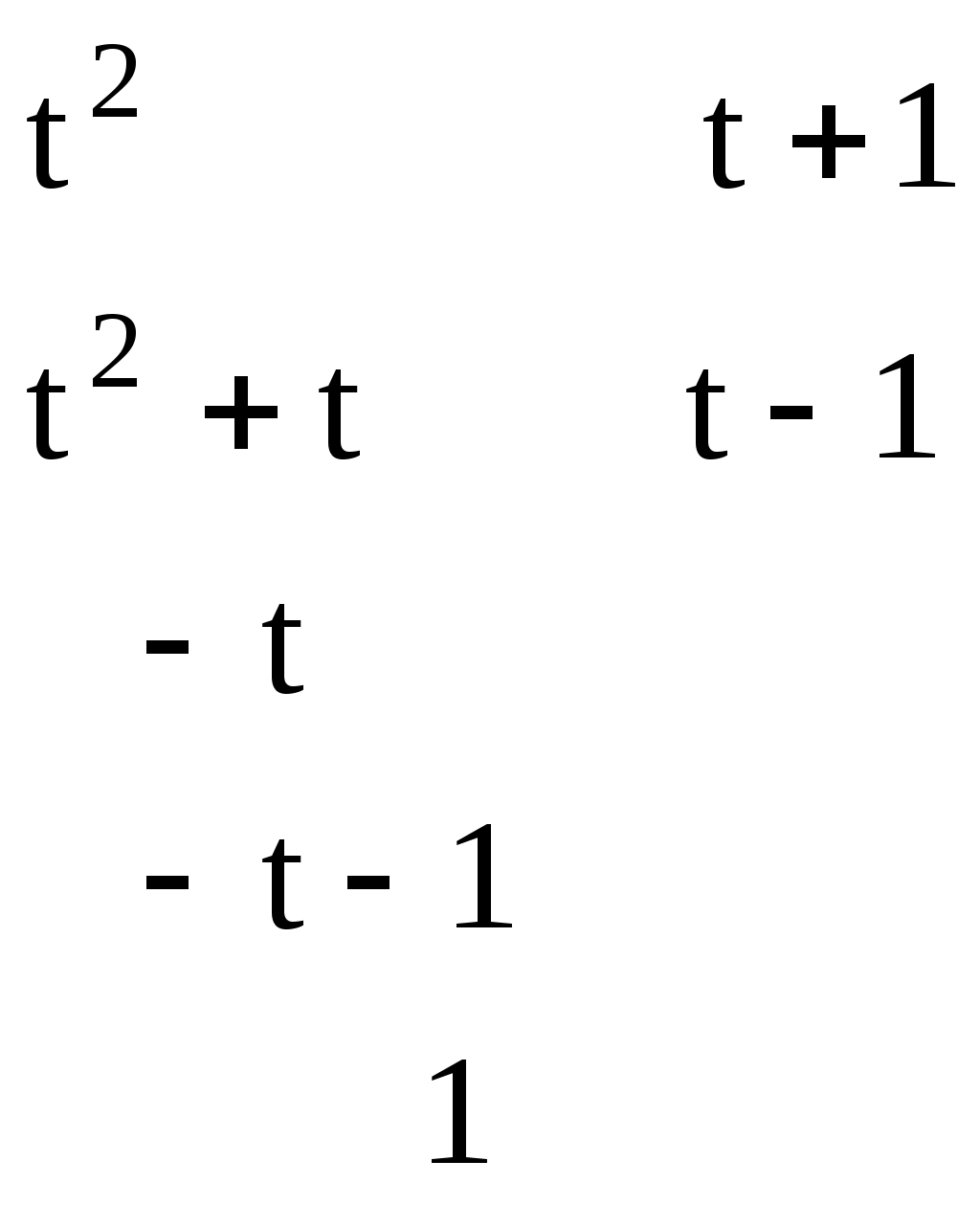  Вычисляем определенный интеграл  8 Вычислить несобственные интегралы или доказать их расходимость: 8.14 а)  Несобственный интеграл с бесконечными пределами интегрирования (1 рода)  от функции y=f(x) на полуинтервале  называется предел функции Ф(t) при  Если такой предел существует и конечен, то несобственный интеграл называется сходящимся к данному пределу. Если конечного предела не существует, то несобственный интеграл называется расходящимся.  Решим неопределенный интеграл  Проведем замену t = x2 + 4x + 1, отсюда dt = (x2 + 4x + 1)′dx = (2x + 4)dx,  , тогда Применили табличную формулу интегрирования  Проведем обратную замену t = x2 + 4x + 1 Получаем решение неопределенного интеграла  Решение несобственного интеграла:  Данный интеграл сходится б)  Если функция f(x) непрерывна при a ≤ x < b и имеет точку разрыва x = b, тогда  Подынтегральная функция терпит бесконечный разрыв в точке  . Решаем несобственный интеграл 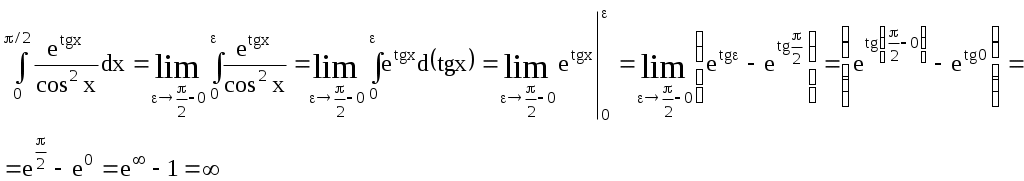 Данный интеграл расходится Учли в решении табличный интеграл  |