Идз 2 Вариант 0 Найти y и y
 Скачать 59.14 Kb. Скачать 59.14 Kb.
|
 ИДЗ 6.2 – Вариант 0 1. Найти y′ и y″ 1.0 y2 = 15x2 + 9 Продифференцируем обе части по x: 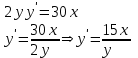 Заметим, что производная неявной функции выражается через х и у, то есть получается равенство y' = g(x, y) (1) Для вычисления второй производной неявной функции, нужно продифференцировать обе части равенства (1) по х и затем подставить выражение g(x, y) вместо y'. 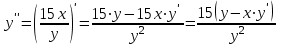 Подставим 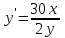 вместо y', получим вместо y', получим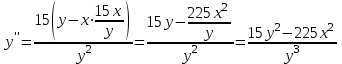 2. Найти y′ и y″ 2.0 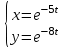 Пусть функция у от х задана параметрическими уравнениями: x = x(t), y = y(t), t  (a;b). (a;b).Предположим, что функции x(t), y(t), имеют производные на (a;b) и функция x(t) имеет обратную функцию t = g(х), которая также имеет производную в соответствующих точках х. Тогда определенную параметрическими уравнениями функцию у от х можно рассматривать как сложную функцию y = y(t), t = g(х), t– промежуточный аргумент. По правилу дифференцирования сложной функции получаем y'x = y't t'x = y't g'x. По теореме о дифференцировании обратной функции 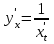 . Учитывая это, получаем . Учитывая это, получаем 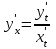 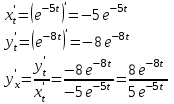 Вторая производная 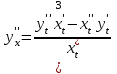 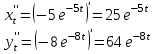 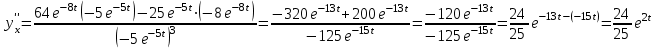 3. Для данной функции y и аргумента x0 вычислить y′′′(x0) 3.0 y = xcos4x, x0 = π Последовательно находим 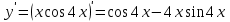 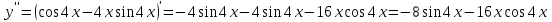 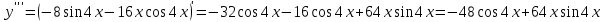 Подставляем в функцию y′′′(x0) значение аргумента x0, получим 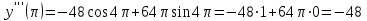 4. Записать формулу для произвольной n-го порядка указанной функции. 4.0 y = 9x Дифференцируя последовательно n раз данную функцию, находим 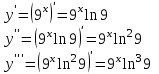 Сравнив полученные выражения для 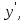 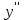 и и 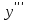 , запишем: , запишем: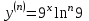 5. Решить следующие задачи. 5.0 Записать уравнение касательной к кривой y = x3 − 8x2 + 2x – 13 в точке с абсциссой x=2 Уравнение касательной: 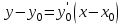 Найдем y0 и 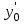 Ордината точки касания 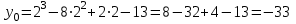 В любой точке 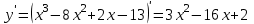 В точке касания 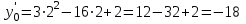 Уравнение касательной будет иметь вид: 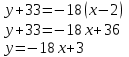 6. Решить следующие задачи. 6.0 В какой точке параболы y2 = 9x ордината возрастает втрое быстрее, чем абсцисса? Решение: Скорость возрастания ординаты 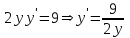 Скорость возрастания ординаты в 3 раза больше скорости абсциссы 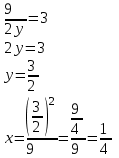 Ответ: 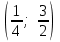 |
