практическая работа по теме производная. 7.12.2020 Урок на тему Исследование и построение графика функии.. Исследование функции с применением первой и второй производной монотонность, критические точки, выпуклость графика функции, точки перегиба
 Скачать 139.38 Kb. Скачать 139.38 Kb.
|
|
Урок на тему Применение производной к построению графиков функции. Исследование функции с применением первой и второй производной: монотонность, критические точки, выпуклость графика функции, точки перегиба. Задание: Ответить на вопросы (устно) Изучить и записать схему исследования функции. Разобрать пример, приводимый в лекции исследования и построения графика функции с помощью производной. Самостоятельная работа: исследовать и построить графика функции с помощью производной по схеме. (задание выполнить по образцу примера из лекции, выполненную работу прислать на проверку) Урок Дифференциальное исчисление – это раздел математики, в котором изучаются производные и их применение к исследованию функций. Приращения вида, представляющие собой разности, играют заметную роль при работе с производными. Поэтому естественно появление латинского корня differentia (разность) в названии calculis differentialis нового исчисления. Термин «производная» является буквальным переводом на русский язык французского слова derivee, которое ввел в 1797 году Ж. Лагранж. Он же ввел современные обозначения и. Г. Лейбниц говорил о дифференциальном отношении и обозначал производную как df/dx. Это обозначение встречается и в современной литературе. Ученые, внёсшие значительный вклад в развитие дифференциального исчисления: Н. Тарталья, Г. Галилей, Р. Декарт, Д. Грегори, И. Ньютон, Г. Лейбниц, Я. Бернулли , Г. Лопиталь ( краткое изложение о вкладе в понятие производной каждого). Лозунгом многих математиков XVII века был: «Двигайтесь вперед, и вера в правильность результатов к вам придет!» На прошлом уроке изучили алгоритмы исследования функции на монотонность и экстремумы, выпуклость и точки перегиба. Выполнили самостоятельную работу. Вспомним ранее изученное Опрос Определение производной … Производная сложной функции Физический смысл первой производной…. Геометрический смысл первой производной…. Физический смысл второй производной…. Определение непрерывной функции Монотонность функции? Признак возрастающей (убывающей) функции Определение критических точек Определение экстремумов функции Алгоритм исследования функции на монотонность Алгоритм исследования функции на экстремумы Определение выпуклости функции Точки перегиба Алгоритм исследования функции на выпуклость (вогнутость) Алгоритм исследования функции на точки перегиба Практические задания для повторения: П 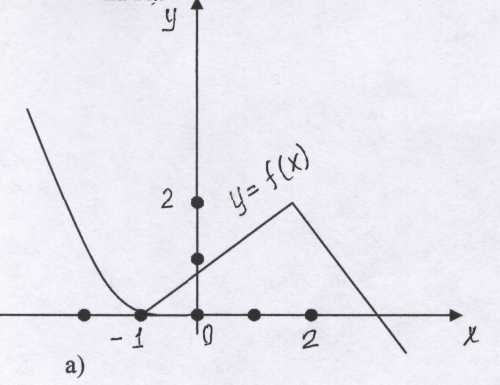  о характеру изменения графика функции (см.рис) укажите, на каких промежутках производная положительна, на каких отрицательна (каждая из функций определена на R). 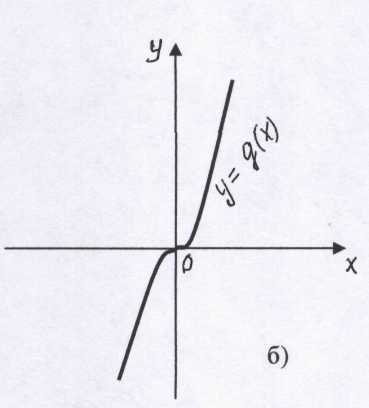 2) На каких промежутках функции f(x) и g(x) возрастают, а на каких убывают?  Изучение нового материала Запишем в тетради схему исследования функции, которая позволит строить график по наименьшему количеству точек. Общая схема построения графиков функций 1. Найти область определения функции 2. Выяснить, не является ли функция четной, нечетной. Периодической. 3. Найти точки пересечения графика с осями координат (нули функции. 4. Найти асимптоты графика функции. 5. Найти промежутки монотонности функции и ее экстремумы (Таблица 1). 6. Найти промежутки выпуклости графика функции и точки перегиба (Таблица 2). 7. Построить график, используя полученные результаты исследования. Замечание: В пунктах 5 и 6 построить таблицы интервалов и крайних точек. В точках найти значение функции. Таблица 1 для монотонности и экстремумом функции
Таблица 2 для выпуклости и точек перегиба функции
Пример исследования функции и построения графика с помощью производной Дана функция: f(x) =у = х3 -6х2 + 9х – 3. Исследовать по схеме, заполнить таблицы и построить график. Решение: 1) D (у) = R. f(-x) = (-х )3 -6(-х)2 + 9(-)х – 3≠f(x) ≠-f(x) - ни четная, ни нечетная, не периодическая. Точки пересечения с осями координат: Ось Ox: (точки пересечения графика функции с осью Ox можно найти, решив уравнение х3 -6х2 + 9х – 3=0. Ho это довольно сложно, т.к. абсциссы точек пересечения - дробные числа. Ось Oy: х = 0 f(0) =03 -6*02 + 9*0 – 3=-3 y(0) = - 3; (0; - 3) 4)Асимптоты -нет 5) f‘(х) = Зх2 - 12х + 9; Критические точки: a) D (f'(x) )=R, б) f'(x) = 0; 3(х2 -4х + 3) = 0; х =1; х = 3. в)отмечаем на числовой оси критические точки и определяем знак производной на каждом интервале 
f ‘(х) < 0 на интервале (1; 3), следовательно , f(x) убывает на [ 1 ; 3 ]; f’ (х) > 0 на интервалах (-∞ ,-1) и (3 ;+∞): f(x) возрастает на (-∞; 1] и [ 3;+∞). г) значения функции в критических точках: f(1) =13 -6*12 + 9*1 – 3=1 f(3) =33 -6*32 + 9*3 – 3=-3 6)f"(x) = 6х - 12; a) D (f"(x) )=R, б) f"(x) = 0; 6х-12 = 0; х = 2-точка перегиба в) Отмечаем на числовой оси точки перегиба и знаки второй производной на каждом интервале 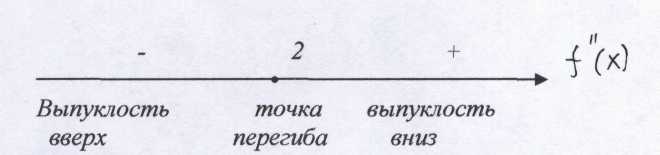
г) значения функции в точках перегиба: f(2) =23 -6*22 + 9*2 – 3=-1 7. Строим график используя значения координат точек, монотонность, выпуклость. Итог урока Изучили схему исследования функции: Перечислить пункты исследования Как найти участки возрастания (убывания) функции Как найти критические точки Как найти участки выпуклости (вогнутости) функции Как найти точки перегиба Что называют нулями функции. Как их определить? Как найти асимптоту. Виды Исследуем функцию – зачем? Для чего нам исследовать функцию с помощью производной? Затем, чтобы лучше понять, как выглядит ее график. Средства математического анализа позволяют досконально исследовать неизвестную функцию. Не разобрав подробно по полочкам все характеристики функции и ее производной верный график не построить. Самостоятельная работа
|