Главная страница
Навигация по странице:

  • 1 Цель обучения

  • Критерийоценивания Обучающийся

  • Уровень мыслительных Применение навыков Навыки высокого порядкавремя выполнения - 20 мин

  • Критерий оценивания №задания

  • Итого 14

    		•

    сор по алгебре 10 класс Применение производной. Тема Признаки возрастания и убывания функции


    Скачать 51.89 Kb.
    НазваниеТема Признаки возрастания и убывания функции
    Анкорсор по алгебре 10 класс Применение производной
    Дата13.05.2022
    Размер51.89 Kb.
    Формат файлаdocx
    Имя файлаsor-po-algebre-i-nachalam-analiza-za-10-klass-primenenie-proizvo.docx
    ТипИсследование
    #526399

    ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ
    Суммативное оценивание за раздел «Применение производной»

    Тема Признаки возрастания и убывания функции

    Критические точки и точки экстремума функции Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость Исследование функции с помощью производной и построение графика

    Наибольшее и наименьшие значения функции на отрезке

    1
    Цель обучения
     0.04.1.26 Знать необходимое и достаточное условие     возрастания (убывания) функции на интервале.

    10.04.1.27 Находить промежутки возрастания (убывания) функции

    10.4.1.29 Знать определения критических точек и точек экстремума функции, условие существования экстремума функции

    10.4.1.31 Знать определение точки перегиба графика функции и необходимое и достаточное условие выпуклости вверх (вниз) графика функции на интервале

    10.4.1. 33 Исследовать свойства функции с помощью производной и строить её график.


    Критерийоценивания Обучающийся:

    • Использует условие возрастания (убывания) функции и находит промежутки монотонности

    • Использует

    • определение точек экстремума функции

    • Находитточкиперегибаграфикафункции

    • Строитграфикфункции

    • Решает задачи на нахождение наибольшего (наименьшего) значения функции

    Уровень мыслительных Применение

    навыков Навыки высокого порядка

    время выполнения - 20 мин

    1 вариант

    1. Дифференцируемая функция может иметь экстремум в тех точках, где: 

    1)производная не существует; 2) производная равна нулю;

    3) производная равна нулю и не существует.
    2. На рисунке изображён график производной функции, определённой на

    интервале (-7; 4). Определите промежутки возрастания и убывания функции.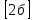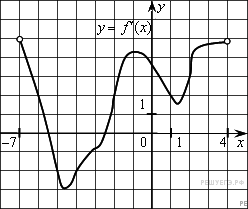



    3. Для функции f(x) =х3 – 2х2 + х + 3

    а)Найдите экстремумы функции;

    б) Найдите интервалы возрастания и убывания функции

    в) Найдите точки перегиба

    г) Постройте график функции f(x) = х3- 2х2 +х +3 на отрезке .

    д) Найдите наибольшее и наименьшее значения функции f(x) = х3- 2х2 +х +3 на отрезке .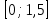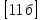

    2 вариант

    1. Если на интервале функция возрастает, то значение производной на этом интервале:

    1) равно нулю; 2) больше нуля; 3) меньше нуля.

    2. На рисунке изображён график производной функции, определённой на

    интервале (-6; 8). Определите промежутки возрастания и убывания функции.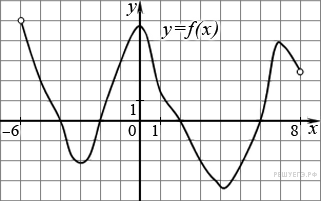


    3. Для функции f(x) = х3- х2 - х +2.

    а)Найдите экстремумы функции;

    б) Найдите интервалы возрастания и убывания функции

    в) Найдите точки перегиба

    г) Постройте график функции на отрезке .

    д) Найдите наибольшее и наименьшее значения функции f(x) = х3- х2 - х +2 на отрезке .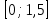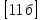

    Критерий оценивания
    №

    задания
    Дескриптор
    Балл

    Обучающийся

    Использует условие

    возрастания (убывания) функции
    1
    Верно использует свойство дифференцируемой функции для ответа на вопрос
    1

    2
    Находит промежутки возрастания функции
    1

    Находит промежутки убывания функции
    1

    Использует

    определение точек

    экстремума функции
    3(а)
    находит производную функции;
    1

    использует определение точек

    экстремума для составления выражения;
    1

    Использует условие

    возрастания (убывания) функции и находит промежуткимонотонности
    3(б)
    находит промежутки возрастания;
    1

    находит промежутки убывания;
    1

    Находит точки перегиба графика функции
    3(в)
    находит вторую производную функции;
    1

    составляет и решает уравнение;
    1

    определяет точки перегиба;
    1

    Строит график

    функции
    3(г)
    изображает точки пересечения с осями координат;
    1

    строит эскиз графика функции;
    1

    Находит наибольшее и наименьшее значения функции
    3(д)
    Находит значение функции на концах промежутка и в критических точках
    1

    Определяет наибольшее и наименьшее значения функции
    1

    Итого
    14

    Скачано с www.znanio.ru

    написать администратору сайта