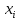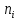Контрольная работа по высшей математике. Контрольная по высшей матеиатике. Решение Задание 2

• Название: Решение Задание 2
• Анкор: Контрольная работа по высшей математике
• Дата: 24.01.2022
• Размер: 3.69 Mb.
• Имя файла: Контрольная по высшей матеиатике.docx
• Тип: Решение; #340445

Вариант 4
Задание 1.

Вычислить пределы





Решение: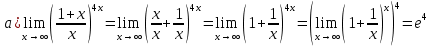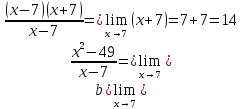




Задание 2.

Найти точки максимума, минимума и точки перегиба и указать промежутки возрастания и убывания для графика функции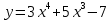



Решение:

1. Находим интервалы возрастания и убывания:

Первая производная.

f '(x) = 12x³+15x²

f '(x)=x²·(12x+15)

Нули функции.

x²·(12x+15) = 0

x₁ = 0, x₂ = -5/4.

f (x) возрастает на (-5/4; 0), (0; + ∞)

f(x) убывает на (-∞; - 5/4).

Так как около точки х= - 5/4 f '(x) меняет знак, значит точка минимума: х_min= - 5/4. Точки максимума не будет так как f (x) стремиться к бесконечности.

2. Находим интервалы выпуклости и вогнутости функции.

Вторая производная.

f ''(x) = 12x²+2x·(12x+15)

f ''(x) = 6x·(6x+5)

Находим точки перегиба.

6x·(6x+5) = 0

x₁ = 0

x₂ = -5/6

f (x) вогнута на (-∞; - 5/6), (0; + ∞).

f (x) выпукла на (-5/6; 0).
Задание 3.

Вычислить площадь фигуры, ограниченной линиями: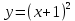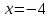

; ; ;

Решение:

– парабола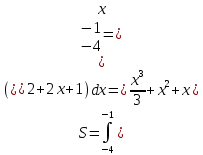


Задание 4.

Найти частные производные функции: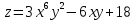



Решение:

Находим частные производные:

При нахождении ∂z/∂x считаем аргумент y постоянным: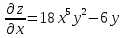



При нахождении ∂z/∂y считаем аргумент x постоянным:



Найдем смешанные частные производные:

Для того, чтобы найти ∂²z/∂x∂y дифференцируем ∂z/∂x по у:


Задание 5.

Решить систему уравнений методом Гаусса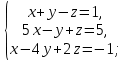



Решение:

Матричный вид записи: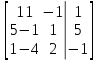



Исключим элементы 1-го столбца матрицы ниже элемента a_1,1. Для этого сложим строки 2,3 со строкой 1, умноженной на -5,-1 соответственно:



Исключим элементы 2-го столбца матрицы ниже элемента a_2,2. Для этого сложим строку 3 со строкой 2, умноженной на -5/6:



Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):



Из расширенной матрицы восстановим систему линейных уравнений: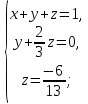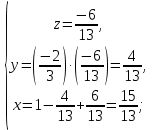







Задание 6.

Вычислить: ; ;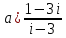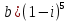

c) представить число в тригонометрической форме: . Постройте радиус вектор в комплексной плоскости.
Решение:



Принимаем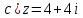





Тригонометрическая форма:




Задание 7.

Найти общее решение дифференциального уравнения:



Решение:



Общее решение дифференциального уравнения: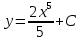


Задание 8.

Выборка задана в виде распределения частот:

	12	8	10
	6	4	10

Найти распределение относительных частот. Построить полигон частот.
Решение:

Распределение относительных частот:

		Относительные частоты,
12	6	0,3
8	4	0,2
10	10	0,5
Итого:	20	1

Полигон частот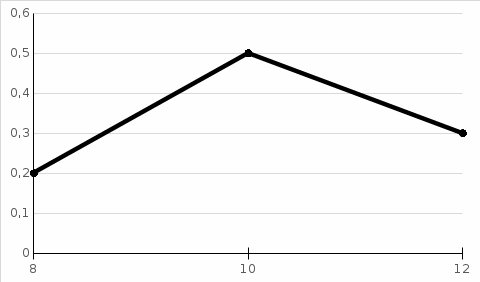


Задание 9.

Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения:

X	6	3	7	4
p	0,4	0,3	0,1	0,2

Решение:

1. 
   Математическое ожидание
   

2. 
   Дисперсия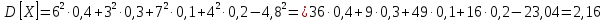
   

3. 
   Среднее квадратическое отклонение